Школа / 10[1]

1. Закон отражения Луч падающий и луч отраженный лежат в одной плоскости с нормалью, проведенной к

отражающей поверхности в точке падения луча. При этом угол падения равен углу отражения.

SО = ОS′

Нормаль (перпендикуляр)

Плоское зеркало

S

S′

О

к отражающей поверхности

S

S′— изображение светящейся точки S в

Угол падения

Угол отражения

плоском зеркале — точка пересечения

α = β

продолжений всех лучей, отраженных

от зеркала — наблюдателю кажется,

В′

А′

α

β

что лучи, попадающие в его глаз,

В

Отраженный

приходят из точки S′

Падающий

луч

луч

Глаз

Изображение точки в плоском зеркале лежит на перпендикуляре,

наблюдателя

проведенном к зеркалу из этой точки, причем,

А

расстояния до зеркала от точки и от ее изображения одинаковы.

2. Закон преломления

Изображение предмета симметрично самому предмету относительно плоскости зеркала

При переходе из одной прозрачной среды в другую световой луч частично отражается от границы раздела сред, а частично проходит в

следующую среду, причем, в новой среде направление луча может измениться. Такой луч, изменивший свое направление при переходе в

новую среду, называется ПРЕЛОМЛЕННЫМ лучом.

Луч падающий и луч преломленный лежат в одной плоскости с нормалью,

Угол падения

Нормаль (перпендикуляр)

проведенной к границе раздела сред в точке падения луча. При этом

sin α

к границе раздела сред

отношение синуса угла падения к синусу угла преломления

α

есть величина постоянная для данных двух сред

sin

β

α

Отраженный луч

при данной частоте излучения.

абсолютный показатель

Падающий

sin α

vсвета1

n2

луч

(результат

= n21 =

=

преломления второй среды

частичного

абсолютный показатель

отражения)

sin β

vсвета 2

n1

преломления первой среды

Преломленный

Абсолютный показатель

β

луч

Относительный

Отношение скорости

преломления – показатель

Угол преломления

преломления среды относительно

показатель преломления

света в первой среде к

вакуума:

с

(показатель преломления

скорости света во второй

n

=

n2 > n1

; α > β

n2 < n1 ; α < β

второй среды относительно

первой)

среды

vсвета всреде

Среда 1

Среда 1

При переходе луча

8

α

(воздух)

α

(стекло)

в оптически менее плотную среду (n2 < n1)

Скорость света в вакууме с ≈ 3 10

м/с

n1

n1

может произойти ПОЛНОЕ ОТРАЖЕНИЕ

vсвета в воздухе

≈

с, т. е.

nвоздуха ≈ 1

луча от границы раздела сред, если угол

α0 − угол полного внутреннего отражения

n2

n2

β

падения слишком велик: α ≥ α0

при угле падения α = α0

= n2

Среда 2 (воздух)

n2 < n1

α < β

Среда 2

Среда 2

угол преломления β0 = 90о sin α0

β

(вода)

(воздух)

β0 = 90о

n1

При переходе луча в

При переходе луча в

α0

α > α0

sin α0

= 1

оптически более

оптически менее

плотную среду

плотную среду

n1

Среда 1

(вода)

n

(n2 > n1)

(n2 < n1)

если луч выходит в

луч приближается к

луч отдаляется от

При углах падения меньших, чем α0,

При α ≥ α0 луч

воздух или вакуум из

нормали

нормали

луч отражается от границы раздела

полностью отражается от

среды с показателем

n1 sin α1 = n2 sin α2 = … = const

сред лишь частично (с ростом α доля

границы раздела сред и не

преломления n

отраженной энергии растет)

выходит во вторую среду

R2

и R1 берутся со

произведение показателя преломления среды на синус угла между лучом и нормалью в этой среде

знаком «+», если

остается неизменным при переходе из одной среды в другую

R2

сфера выпуклая,

4. Линза— прозрачное тело, ограниченное двумя сферическими поверхностями.

«−» - если вогнутая

А

В

О1

Линза считается тонкой, если ее толщина АВ мала по сравнению с радиусами R1 и R2 сферических

О2

поверхностей, ограничивающих линзу, а также по сравнению с расстояниями d и f от линзы до

предмета и от линзы до изображения.

Главная оптическая ось линзы – прямая,

R1

Линза называется собирающей, если лучи, падающие на нее

проходящая через центры О1 и О2 сферических

параллельно друг другу, после преломления сходятся.

поверхностей, ограничивающих линзу.

Линза называется рассеивающей, если лучи, падающие на нее

Обозначение тонкой собира-

Обозначение тонкой рассеива-

параллельно друг другу, после преломления расходятся.

ющей линзы

ющей линзы

Фокусом линзы называется точка, в которой после преломления

O

F

Фокус линзы

F

пересекаются лучи, упавшие на линзу параллельно ее главной

O

оптической оси (или продолжения преломленных лучей, если

линза рассеивающая).

1

1

1

Фокусное расстояние

Оптическая сила линзы

линзы – расстояние от

измеряется в диоптриях:

D =

=

nлинзы

+

F

−1

± R1

F > 0

линзы до фокуса.

F < 0

1 дптр = 1/м = 1м-1

nсреды

± R2

F

В СИ измеряется в метрах.

F

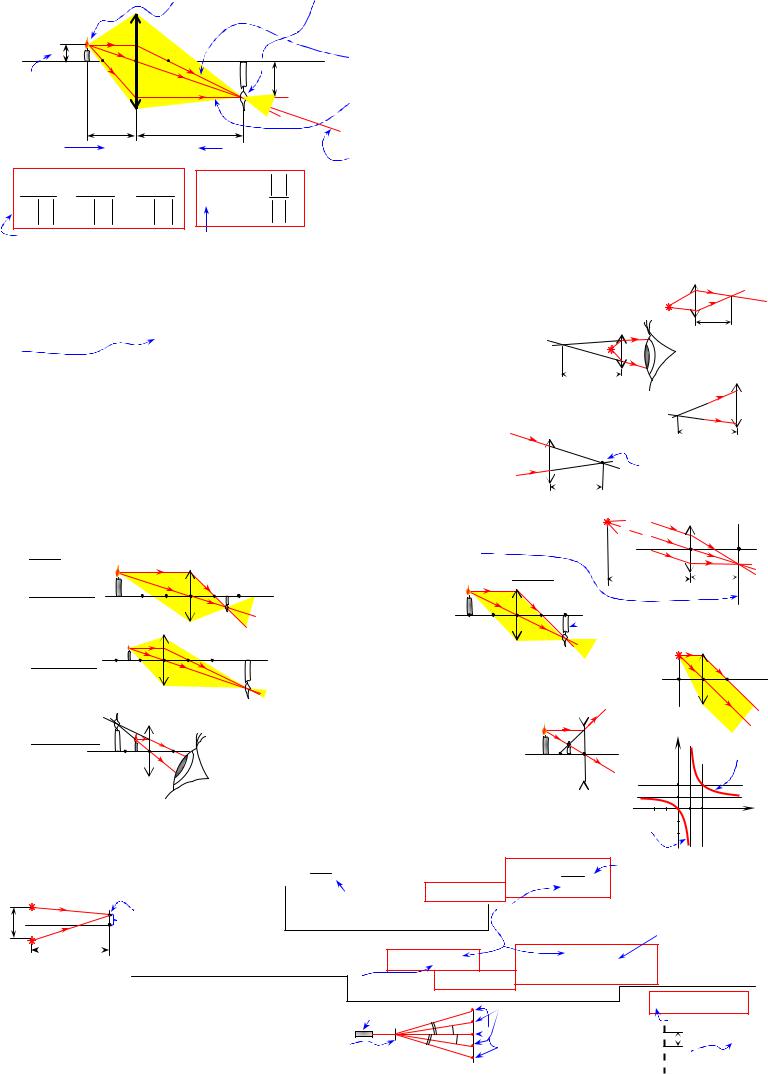
5. Изображение точки S в линзе – это такая точка S′, в которой лучи, вышедшие из точки S, пересекаются после преломления в линзе.

Чтобы построить изображение S ′ точки S, надо знать ход двух лучей,

S

вышедших из S и преломленных в линзе (где пересекутся эти лучи, там

h

F

пересекутся и все остальные). Всегда известен ход следующих лучей:

O

A′

A

F

• луч, падающий на линзу параллельно главной оптической оси,

размер

Н – размер

преломившись, проходит через фокус (если линза собирающая) или идет

так, что его продолжение проходит через фокус (если линза рассеивающая)

изобра-

предмета

• луч, падающий на собирающую линзу, по прямой, проходящей через фокус,

S′

жения

(луч, падающий на рассеивающую линзу вдоль прямой, проходящей через

фокус, расположенный с другой стороны линзы) преломившись, идет

расстояние

d

f

расстояние

параллельно главной оптической оси

от линзы до предмета

от линзы до изображения

• луч, проходящий через оптический центр тонкой линзы, после преломления

1

1

1

H =

f

практически не отклоняется от прямой, вдоль которой он упал на линзу.

+

=

Γ =

Если показатель преломления среды одинаков с обеих сторон линзы, то

оптический центр (точка О на рисунке) – пересечение главной оптической

± d

± f

± F

h

d

оси с плоскостью тонкой линзы.

Формула тонкой линзы

Линейное (поперечное) увеличение — отношение размера изображения (H) к размеру предмета (h),

Расстановка знаков в

когда предмет — отрезок, перпендикулярный главной оптической оси.

Перед фокусным расстоянием F : «+» — если линза собирающая, «−» — если линза рассеивающая.

формуле тонкой линзы:

Перед расстоянием f от линзы до изображения: «+» — если изображение действительное, т. е. лучи от

S

S′

точечного источника после преломления в линзе сходятся:

«−» — если изображение мнимое, т. е. лучи от точечного источника

S ′

S

f > 0

его нельзя получить

после преломления в линзе расходятся.

В этом случае изображением

глаз видит мнимое

на экране, как

считается точка пересечения продолжений преломленных лучей S ′ (именно

действительное

изображение S′

в этой точке видится источник света глазу, в который попадают преломленные лучи)

f < 0

изображение

Перед расстоянием

d от линзы до предмета: «+» — если предмет действительный, т. е. лучи от точечного

S

источника падают на линзу расходящимся конусом:

«−» — если предмет мнимый, т. е. лучи от точечного источника

d > 0

падают на линзу сходящимся конусом (это возможно, например,

S

мнимый предмет

если лучи предварительно прошли через собирающую линзу).

В этом случае предметом считается точка пересечения продолжений лучей,

d < 0

упавших на линзу.

6. Возможные случаи расположения предмета:

S

6.1. d → ∞ (т. е. d >> F ) В этом случае лучи от точечного источника идут практически параллельно друг другу.

F

f = F — изображение точечного источника находится в фокальной плоскости.

S′

6.2. d (2F; ∞)

Изображение:

6.3. d = 2F ; f = 2F

…

f = F

f (F; 2F)

F

2F

действительное (f > 0 ),

d → ∞

(фотография)

2F

F

перевернутое,

F

2F

уменьшенное (|d| > | f | Γ < 1)

2F

F

Размер изображение равен

размеру предмета (d = f, Γ = 1)

6.4. d (F; 2F)

Изображение:

F

2F

S

f (2F; ∞)

действительное (f > 0 ),

6.5. d = F ;

2F

F

f → ∞ - лучи от источника,

F

(кино,

перевернутое,

лежащего в фокальной плоскости,

увеличенное (|d| < | f | Γ > 1)

F

диафильм)

преломившись, идут параллельно.

6.6. d (0; F)

Изображение:

6.7. Рассеивающая линза:

Для собирающей

f (− ∞; 0)

F

мнимое (f < 0 ),

Изображение:

линзы:

f

(лупа)

F

прямое,

мнимое (f < 0 ),

перевернутое

увеличенное (|d| < | f | Γ

> 1)

прямое,

F

уменьшенное (|d| > | f | Γ < 1)

2F

7. Интерференция— наложение волн, при котором эти волны в одних точках усиливают друг друга,

F

d

F 2F

а в других — ослабляют друг друга, так, что интенсивность результирующей волны не равна сумме интенсивностей

прямое

складывающихся волн (I ≠ I1 + I2) Наблюдать интерференцию можно только при наложении когерентных волн.

Когерентными называются волны, разность фаз (ϕ2 – ϕ1) которых в точке наложения не меняется с течением времени.

Фаза гармонической (монохроматической) волны: ϕ=ωt − 2π rопт

+ϕ0 . Для когерентных волн: ϕ

2

−ϕ = 2π ∆

опт

оптическая разность хода

λвак

если ϕ02 = ϕ01

1

λвак

волн от источника до

Чтобы волны были когерентны, необходимо: ω1 =

ω2 rопт - оптическая длина

точки наложения

d S2

r2

M

x

точка наложения волн от

пути волны от источника до точки

Длина накладывающихся

∆

опт

= r

1опт

– r

2опт

источников S

1

и S

наложения волн: rопт = r1n1 + r2n2 + …

световых волн в вакууме

m = 1, 2, 3, …

r1

О

2

Условие минимума:

S1

Разность хода этих волн: ∆ = r1 – r2 = d x/L

Условие максимума:

номер (порядок)

Ширина интерференционной полосы: h = λ L/d

∆опт = m λвак

λвак

L

∆опт =

(2m – 1)

интерференцион-

(расстояние между соседними максимумами)

m = 0, 1, 2, 3, …если ϕ02 = ϕ01

2

ного минимума

8. Дифракция— отклонение от прямолинейного

номер (порядок) интерференционного максимума

d sin αk = k λ

распространения волн при огибании препятствий (прохождении

лазер

максимумы

отверстий). В результате дифракции света возникает картина

α2

α1

первого порядка (k = 1)

период решетки

чередования светлых и темных полос, причем свет может

центральный максимум (k = 0)

d = (10-3/N) м

α2

α1

попасть в зону геометрической тени. Дифракционная решетка −

максимумы

число штрихов

пластинка с чередующимися прозрачными и непрозрачными полосками ( 102 на 1 мм)

второго порядка (k = 2)

на 1 мм