Вариат з

1. Сформулировать 1-ю теорему сравнения для несобственных интегралов 1-го рода.

2. Из совокупности всех первообразных у(х) = Г (х +l)dx выбрать те из них, которые не пересекают ось Х.

3. Доказать, что если f(x) — непрерывная периодическая

функция с периодом Т, то

4. Н айти производную функции: F(x)=

5. Найти: sinx

—dx ;

dx ; 3) fx² cosxdx ;

4) TfJiiGidx.

2

6. Найти

7. Доказать, что если F(x)+C , то ff(ax + b)dx = — F(ax + Ь) + С .

О

6. Найти площадь фигуры, ограниченной линиями у = sinx, y=arctgx в области О<х<—, считая абсциссу од-

ной из точек пересечения равной хо = — (фактически хо 1,56 ).

2

6. В 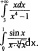ычислить несобственный интеграл или установить его расходимость.

7. Исследовать сходимость интеграла:

Вариант 4

1. Сформулировать 1-ю теорему сравнения для несобственных интегралов 2-го рода.

2. Р ешить уравнение dx, зная, что ,

3. При каких значениях постоянной интегрирования С уравнение Г (2х— l)dx = I имеет ровно одно решение?

4. Н айти производную функции: Е (х) =cos t²dt .

5. Найти:

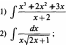dx ;

3) f$dx

2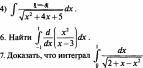

заключен между — и

Найти точное значение интеграла.

8. Найти площадь фигуры lyl —lnlxl,

9. В 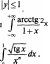ычислить несобственный интеграл 2 dx или установить его расходимость.

10. Исследовать сходимость интеграла:

0

Экзаменационная работа

Оценивание задач: 1—7, 9—10 — 2 балла, 8 — 8 баллов. Длительность экзамена: 120 мин.

Вариант 1

1. Дифференциалы высших порядков. Случаи независимых и зависимых переменных.

2. Сформулировать и доказать 1-ю теорему сравнения для несобственных интегралов 1-го рода.

3. Построить область. D = у = e^ix

и вычислить ее площадь, используя двойные интегралы.

4. Упростить выражение (Е Х (А u (Е \ u (В п (Е \ В)) .

5. Вычислить

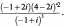
6. Найти производную функции и = х² — ху в точке (1, 1) по направлению [ , задаваемому утлом (У , и построить эпюру Ди

Указать направления, по которым функция имеет

наибольшее изменение.

7. Построить на координатной плоскости фрагмент карты градиентов функции и для > 0, х2 > 0 , если и = +х2 .

8. Найти интеграл:

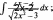
2. fcos⁴ xdx ;

О

2. Г 2 —х² +2x+ldx;

3. г Х4 — 6Х3 -4-12Х2 6dx .

^Ј х^з —6х² +12х—8

9. Найти площадь фигуры, которая задается на координатной плоскости условиями: cosx < у < sinx, 0 < х < — .

10. В ычислить несобственный интегралили установить расходимость.

Вариант 2

1. Формула Ньютона—Лейбница (с выводом).

2. Понятие двойного интеграла. Основные свойства двойно-

го интеграла.

3. Построить область D = х² —lxl S l—x² и вычислить

ее площадь, используя двойные интегралы.

4. Упростить выражение \ А) U В) п ((Е \ А) U (Е \ В)) .

5. Вычислить (1 +i)¹⁰

6. Построить на координатной плоскости фрагмент карты градиентов функции И=Х1 —х2 для > 0, х) > 0 .

7. Найти производную функции и = C2x ¹² y^Y2 в точке (1, 1)

по направлению , задаваемому углом , и построить эпюру ди

= Указать направления, по которым функция имеет

н аибольшее изменение. 8. Найти интегралы: 1) 15. ^з (3x+5)² dx;

6х2

—dx ;

9. Найти площади двух замкнутых фигур, которые образу-

ются при пересечении фунюдий у arcsinx и у = ² х ² , считая 2

а бсциссу одной из точек пересечения равной хо — — (фактически хо х 0,71 ).

9. Вычислить несобственный интегралили установить расходимость.

Вариант З

1. Понятие несобственного интеграла 1-го рода. Эталонный интеграл 1-го рода.

2. Булева алгебра. Операции над элементами. Таблица истинности.

3. П остроить 1) = < min(tgx, ctgx), О <х<— об2 ласть и вычислить ее площадь, используя двойные интегралы.

4. Упростить выражение

6. Найти угол между градиентами функции Z = ln— в точках

0,25) и ВО, 1). х

6. Построить на координатной плоскости фрагмент карты градиентов функции и = для .Xl > 0, Х2 > 0 .

7. Найти интегралы:

dx .

6. Н айти площадь фигуры, которая задается на координатной плоскости условиями: 2^х < у < 2х .

7. Вычислить несобственные интегралыили установить их расходимость.

Вариант 4

1. Понятие неопределенного интеграла, его свойства (с обоснованием).

2. Показательная форма комплексного числа, формула

Эйлера (с выводом).

1

З. Построить область D = —<у<—, 10 ⁵ и вычислить

х х

ее площадь, используя двойные интегралы:.

4. Доказать равенство А Х С) = (А \ В) U (А п С) .

5. Решить уравнение —8i 0 .

6. Построить на координатной плоскости фрагмент карты градиентов функции и для х) > О, х2 > 0 , если и = х: + х2 .

7. Учитывая непрерывность первообразной, найти интеграл: flxldx

8. Найти интеграл:

1. ——dx 3х+4 ;

Ј 3х+2

2. fcos⁵ xdx ;

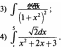
1

9. Найти площадь фигуры, ограниченной линиями

у = sinx, y=arctgx в области 0 < х < — , считая абсциссу одной

ТГ

из точек пересечения равной хо — (фактически хо z 1,56 ).

2

9. Вычислить несобственный интеграл или установить расходимость. 0

Вопросы для оценивания порогового уровня знаний студента в комиссии

Каждый пункт — 1 балл.

Условие сдачи экзамена — 15 баллов

1. Сформулировать определение линии уровня функции двух аргументов.

2. Какая фунющя двух переменных называется дифференцируемой?

3. Сформулировать определение дифференциала функции трех аргументов.

4. Сформулировать определение производной по направлению. По какой формуле вычисляется производная по направлению?

5. Что называется градиентом функции? Как направлен градиент по отношению к линии уровня функции?

6. Нарисовать фрагмент карты, линий уровня функции

7. Н айти двойной предел lim или доказать, что он не существует.

8. Найти частные производные 1-го и 2-го порядков функции z 4х2 + зуз +2х2уз +1 .

9. Найти частную производную — и полную производную du дх — функции и = sinxy , где у = у(х) . dx

10. Выписать в развернутом виде дифференциал 2-го порядка функции четырех переменных.

11. Найти частные производные функции Z = z(x, у) , заданной неявно: 3х ² — 2ху + Z ² +yz—l = 0 .

12. Найти дифференциал 2-го порядка от функции, считая аргументы независимыми переменными и = — . du

13. Найти , если и = х = (Ш), у = f3(t) . dt

14. Найти ух функции у = у(х) , заданной неявно:

15. Разложить по формуле Маклорена до членов 3-го порядка включительно функцию Z = sin 2х + cos3x .

16. Что называется неопределенным интегралом от фуню.щи? 17—23. Найти неопределенный интеграл.

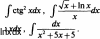, —и fJiGidx,

х

24. Найти у = у(х) из уравнения d(lny)+dx=O, если

24. Зная величину производной функции, определить вид функциональной зависимости .у' = 2 .

25. Что называется средним значением функции на отрезке?

26. Найти производную функции F(x) = lntdt, х > 0 .

27. Оценить интеграл

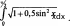
28. Найти площадь фигуры, ограниченной линиями У = З+2Х—Х² , у .

29. Что называется несобственным интегралом 1-го рода?

30. Доказать, что эталонный несобственный интеграл 2-го рода — сходится при р < и расходится при р > .

32—33. Вычислить несобственный интеграл или установить его расходимость е-^ХИ , cosxdx .

3 4—35. Исследовать сходимость интегралов

Список литературы

1. Архипов Г.И., СаДОВНИЧИЙ В.А., Чубариков В.Н. Лекции по математическому анализу. — М.: Высшая школа, 1999.

2. КуДрявцев Л.Д. Краткий курс математического анализа (в 2-х тт.). — М.: АЛЬФА, 1998.

3. Ильин В.А., Позняк ЭМ. Основы математического анализа. — М.: Наука. 1995.

4. Краснов М.Л. и др. Высшая математика (тома 1, 2, 4). — М.: Едиториал УРСС, 2000.

5. Высшая математика для экономистов / Под ред. Н.Ш.Кремера. — М.: Юнит, Банки и биржи, 1998.

6. Ляшко И.И., Боярчук А.К., Гай Я.Г., Гловач ГЛ. Справочное пособие по высшей математике (том 1). — М.: Едиториал УРСС, 1995.

7. Красс МС. Математика для экономических специальностей. — М.: ДЕЛО, 2002.