Тема 5. Экстремумы функции
Теоремы о возрастании и убывании функции на промежуже (с доказательством).
Локальный и абсолютный экстремумы функции. Необходимое условие локального экстремума (с доказательством).
Первое достаточное условие локального экстремума (с доказательством).
Второе достаточное условие локального экстремума (с доказательством).
Понятие выпуклости функции. Теорема о выпуклости функции (с доказательством). Точки перегиба. Необходимое и достаточное условие перегиба (формулировки).
Определение вертикальной, горизонтальной, наклонной асимптот. Примеры.
Схема исследования функции. Построение графиков функций по результатам исследования.
Эластичность. Свойства эластичности. Геометрическая интерпретация. Эластичность функций
.
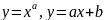2-й семестр
Функции нескольких переменных
Тема 1. Функции нескольких переменных.
Основные понятия функции нескольких переменных, окрестность точки, линия уровня, предел, непрерывность.
Приращения, частные производные, геометрический смысл частной производной.
Определение дифференцируемости. Теорема о существовании частных производных у дифференцируемой функции.
Теорема со связи между дифференцируемостью и непрерывностью функции.
Дифференциал функции.
Однородные функции. Теорема Эйлера.
Производные сложных фующий.
Производная по направлению. Вывод формулы производной по направлению.
Градиент и его свойства.
Производные высших порядков.
Дифференциалы высших порядков.
Производные неявных функций.
Формула Тейлора (с выводом).
Интегральное исчисление
Тема 2. Неопределенный интеграл
Первообразная. Теоремы о первообразной.
Понятие неопределенного интеграла, его свойства (с обоснованием).
Таблица интегралов с выводом любой из формул таблицы. 17. Метод подведения под знак дифференциала.
Методы замены переменной и интегрирования по часММ.
Метод неопределенных коэффициентов нахождения неопределенного интеграла.
Интегрирование рациональных дробей и некоторых видов иррациональностей.
Тема З. Определенный интеграл
Задача о нахождении площади криволинейной трапеции.
Интегральная сумма, определенный интеграл.
Свойства определенного интеграла (с обоснованием).
Определенный интеграл как функция верхнего предела. Его свойства (с доказательством).
Формула Ньютона—Лейбница (с выводом).
Методы нахождения определенного интеграла (формула замены переменной и формула интегрирования по частям, с выводом).
Приближенное вычисление интегралов. Оценка интегралов.
Вычисление площадей плоских фигур.
Тема 4. Несобственные интегралы
Понятие несобственного интеграла 1 -го рода. Эталонный интеграл 1-го рода.
Понятие несобственного интеграла 2-го рода. Эталонный интеграл 2-го рода.
1-я теорема сравнения несобственных интегралов 1-го рода.
1-я теорема сравнения несобственных интегралов 2-го рода.
2-я теорема сравнения несобственных интегралов 1-го рода.
2-я теорема сравнения несобственных интегралов 2-10 рода.
Абсолютно и условно сходящиеся интегралы. Сходимость несобственного интеграла от знакопеременных функций.