2.3. Выводы
2.3.1. Построен сигнальный граф 8-точечного алгоритма БПФ с прореживанием по времени для заданной последовательности (рис. 2.2). Из полученного графа видно, что базовая операция «бабочки» 2-точечного ДПФ формирует основу для всего вычисления спектральных коэффициентов. Вычисление осуществляется в три стадии. После того, как заканчивается вычисления на первой стадии, нет необходимости сохранять какие-либо предыдущие результаты. Результаты вычислений первой стадии могут быть сохранены в тех же самых регистрах или ячейках памяти, которые первоначально хранили отсчеты из временной области. Точно так же, когда заканчивается вычисления на второй стадии, результаты вычислений, полученные на первой стадии, могут быть удалены. Таким же образом осуществляется вычисления последнего каскада, заменяя в памяти промежуточный результат вычислений предыдущей стадии.
2.3.2. Рассчитаны и изображены на комплексной плоскости поворачивающие множители для каждой из стадий вычисления спектральных коэффициентов (рис. 2.3). Из данного рисунка видно, что на всех стадиях объединения число поворачивающих множителей удваивается, причем все множители предыдущей стадии объединения присутствуют и на следующей стадии. Таким образом, для того чтобы перейти к следующей стадии необходимо между поворачивающими множителями текущей стадии вставить поворачивающий множитель следующей стадии.
2.3.3. С использованием полученного сигнального графа, рассчитаны комплексные спектральные коэффициенты для заданного дискретного сигнала, определены их модули и аргументы. Также рассчитаны спектральные коэффициенты заданного сигнала с помощью MATLAB функции fft и построены графики спектральных характеристик данного сигнала (рис. 2.4––2.5). Сравнивая результаты самостоятельного расчета и расчета с помощью fft, видно, что они полностью совпадают. Идентичность графиков указывает на то, что БПФ не является приближенным алгоритмом. При отсутствии вычислительной погрешности он дает такой же результат, как и прямой метод ДПФ. Ускорение достигается исключительно за счет оптимизации вычислений.
2.3.4. Рассчитан выигрыш БПФ в сравнении с алгоритмом ДПФ по числу операций комплексного умножения и сложения. По результатам расчета можно сделать вывод, что БПФ позволяет значительно сократить время вычислений спектральных коэффициентов, в случае 8-точечной последовательности количество операций умножения уменьшается в 4,1 раза, а количество операций сложения — в 2,33 раза. Чем больше последовательность, тем больше будет выигрыш по числу операций, например, в 1024-точечной последовательности он будет составлять для умножения 204,4 раза, а для сложения –– 102,3 раза.
3. Задание 3
3.1. Постановка задачи
Цель работы:
Линейная дискретная система (ЛДС) задана разностным уравнением
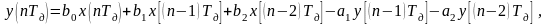(3.1)
где b0, b1, b2, a1, a2 — коэффициенты, определяемые вариантом задания;
TД = 1 мс –– интервал дискретизации сигналов.
Исходные данные для расчета представлены в таблице 3.1.
Требуется:
1. Составить структурную схему ЛДС.
2. На основе обобщенной передаточной функции рекурсивной ЛДС и заданных коэффициентов составить формулу передаточной функции ЛДС. Определить полюса передаточной функции и нанести их на р-плоскости. Сделать вывод об устойчивости ЛДС по положению полюсов на р-плоскости.
3. Составить формулу комплексной частотной характеристики, заданной ЛДС. Вывести соотношения для расчета АЧХ и ФЧХ заданной дискретной системы. Написать скрипт MATLAB, в котором, по полученным соотношениям, с помощью функции plot, построить графики АЧХ и ФЧХ заданной ЛДС. Построить те же графики с помощью MATLAB-функции freqz. Сравнить полученные результаты и сделать выводы.
4. Составить системную функцию заданной ЛДС, определить полюса системной функции и нанести их на z-плоскости, сделать вывод об устойчивости.
5. Рассчитать и построить семь отсчетов импульсной характеристики ЛДС с учетом нулевых начальных условий;
6. Рассчитать и построить десять отсчетов выходного сигнала заданной ЛДС с нулевыми начальными условиями, если на её вход подаётся сигнал из задания №2.
Таблица 3.1 –– Исходные данные
№ |
Коэффициенты разностного уравнения |
||||
b0 |
b1 |
b2 |
a1 |
a2 |
|
03 |
1 |
0,6429 |
0999 |
-1,01 |
0,8 |