Министерство образования и науки Российской Федерации

ФГАОУ ВО «Севастопольский государственный университет»

Институт радиоэлектроники и информационной безопасности

Кафедра «Радиоэлектроника и телекоммуникации»

Курсовая работа

по дисциплине

«Цифровая обработка сигналов»

Вариант №03

Выполнил: студент гр. Р/б-41-о

Голованов Никита Алексеевич

Защитил с оценкой_____________

Принял: асс. кафедры РТ

Снегур Дмитрий Александрович

Севастополь

2017

Содержание

1. Задание №1 3

2. Задание №2 11

3. Задание №3 18

4. Задание №4 28

5. Задание №5 38

Заключение 49

Библиографический список 50

1. Задание 1

1.1. Постановка задачи

Аналоговый сигнал x(t), изображенный на рис 1.1 длительностью T_c = 1 мс подвергнут дискретизации путём умножения на последовательность δ-импульсов. Интервал дискретизации T_Д. Амплитуда сигнала А равна номеру варианта V.

Номер варианта — A = 13 В.

Рис. 1.1 –– Исходный аналоговый сигнал

Требуется:

1) рассчитать спектр аналогового сигнала x(t) и построить график модуля спектральной плотности;

2) определить максимальную частоту в спектре аналогового сигнала f_max, ограничивая спектр по уровню 0,1 от максимального значения модуля спектральной плотности;

3) рассчитать интервал дискретизации T_Д и число отсчетов дискретного сигнала N, которым он представляется на интервале [0, T_с];

4) изобразить дискретный сигнал x_д(nT_Д), где n = 0, 1, …N–1 под аналоговым x(t) в том же временном масштабе;

5) определить спектральную плотность дискретного сигнала x_д(nT_Д) и построить график модуля спектральной плотности под графиком спектра аналогового сигнала в том же частотном масштабе;

6) провести дискретное преобразование Фурье (ДПФ) сигнала x_д(nT_Д), определить комплексные коэффициенты ДПФ и построить спектрограмму модулей этих коэффициентов под графиками спектров аналогового и дискретного сигналов в том же частотном масштабе;

7) сделать вывод о взаимосвязи спектров аналогового и полученного в результате его дискретизации дискретного сигналов.

1.2. Решение задачи

Для начала сформируем наш исходный аналоговый сигнал в программной среде MATLAB. Текст программы для выполнения этого задания:

clear all;

clc;

%Построение заданного аналогового сигнала

A = 03; Ts = 10^-3;

t = 0:Ts/1000:Ts;

for n=1:1:1001

s(n) = A*sin(pi*n*10^(-3));

end

figure(1)

plot(t,s)

ylim([0 13])

title('Исходный аналоговый сигнал')

xlabel('t, c')

ylabel('s(t)')

grid on

Построенный в программной среде MATLAB исходный аналоговой сигнал x(t), изобразим на рис. 1.2.

Рис. 1.2 –– Исходный аналоговый сигнал

Построим график модуля спектральной плотности и на уровне 0,1 от X(ω)_max найдем f_max. Спектральная плотность рассчитывается по формуле 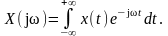(1.1)

(1.1)

Численный расчет спектральной плотности заданного сигнала x(t) можно выполнить методом трапеций с помощью функции MATLAB trapz(x,y). Напишем следующий текст программы:

f=-10000:1:10000;

for k=1:length(f)

x(k)=abs(trapz(t,s.*exp(-1i*2*pi*f(k)*t)));

y(k)=0.1*max(x);

end

figure(2)

plot(f,x,f,y)

title('Спектр аналогового сигнала')

xlabel('f, Гц')

ylabel('|S(jw)|')

grid on

График модуля спектральной плотности изобразим на рис. 1.3.

Рис. 1.3 –– Модуль спектральной плотности исходного сигнала

В этом случае f_max = 1,4 кГц. Воспользуемся теоремой Котельникова, чтобы найти минимальный период дискретизации

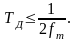(1.2)

Подставляя числовые значения, получим:

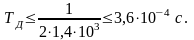
С учетом неравенства (1.2) выберем период дискретизации равный

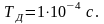
Определим число отсчетов дискретного сигнала по формуле

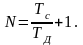(1.3)

Подставляя длительность сигнала и период дискретизации, получим следующее количество отсчетов:

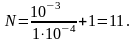
Построим и изобразим на рис. 1.4 дискретный сигнал x(nT_Д). Напишем программу, соответствующую этому заданию:

Td = 1*10^-4;

N = Ts/Td+1

%Построение дискретного сигнала

t1 = 0:Td:Ts;

for n1=1:1:11

s1(n1) = A*sin(pi*(n1-1)*0.1);

end

figure(3)

stem(t1, s1)

title('Дискретный сигнал')

xlabel('nTd, c')

ylabel('s(nTd)')

grid on

Рис. 1.4 –– Дискретный сигнал

Рассчитаем спектральную плотность дискретного сигнала с помощью формулы

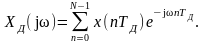(1.4)

Текст программы для этой операции укажем ниже:

%Определение спектральной плотности дискретного сигнала

f=-10000:1:10000;

for k=1:length(f)

x1(k)=abs(trapz(t1,s1.*exp(-i*2*pi*f(k)*t1)));

end

figure(4)

plot(f, x1)

title('Спектр дискретного сигнала')

xlabel('f, Hz')

ylabel('|S1(jw)|')

grid on

Изобразим график модуля спектральной плотности дискретного сигнала на рис. 1.5.

Рис. 1.5 –– Модуль спектральной плотности дискретного сигнала

Так как по теореме Котельникова f_s ≥ 2f_max, а мы выбрали частоту дискретизации 10 кГц, сделаем вывод, что наложение спектра отсутствует и это лучший случай для фильтрации. Однако выбрано слишком большое количество отсчетов и в реальных устройствах это будет занимать большее количество памяти в устройстве. Такая частота дискретизации была выбрана для удобства написания программы.

Дискретное преобразование Фурье определяется соотношением

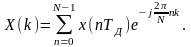(1.5)

В программном пакете MATLAB воспользуемся встроенной функцией fft. Отсчеты спектральной плотности следуют через интервалы

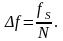(1.6)

Подставив значения, определим интервалы следования отсчетов спектральной плотности

Напишем текст программы для нахождения дискретного преобразования Фурье:

%Выполнение дискретного преобразования Фурье

N=11;

fd = 10000;

n=0:1:10;

y=fft(s1);

figure(5)

Xm = abs(y);

Xmm = 2*abs(y)/N;

for j =1:1:22;

if j < 12

a(j) = Xmm(j);

else

a(j) = Xmm(j-N);

end

end

k = -11:1:10;

stem(k*fd/N,a)

title('Модули коэффициентов ДПФ')

xlabel('f, Hz')

ylabel('|S(k)|')

grid on

График модулей коэффициентов ДПФ представим на рис. 1.6.

Рис. 1.6 –– Модули коэффициентов ДПФ