ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

«Уральский государственный технический университет – УПИ»

Нижнетагильский технологический институт (филиал) угту–упи измерение вязкости жидкости по методу падающего шарика

Методические указания к лабораторной работе №4 по физике для студентов всех специальностей

Нижний Тагил

2007

УДК 532.516+532.13(076)

Составитель: А. А. Ходырев

Научный редактор: Т.М. Гаврилова

Утверждено на заседании кафедры общей физики НТИ (ф) УГТУ – УПИ

(протокол № 4 от 15.05.2007 г.)

Измерение вязкости жидкости по методу падающего шарика. Методические указания к лабораторной работе № 4 для студентов всех специальностей НТИ (ф) УГТУ – УПИ [Текст] / сост. А. А. Ходырев. – Нижний Тагил : НТИ (ф) УГТУ – УПИ, 2007. – 14 с.

В работе описан метод определения вязкости жидкостей по методу падающего шарика. Описан порядок выполнения работы и оформления отчета.

Библиогр.: 8 назв. Рис. 3. Прил. 1.

Подготовлено кафедрой «Общая физика».

 Нижнетагильский технологический институт (филиал) ГОУ ВПО «Уральский государственный технический университет – УПИ», 2007

Введение

В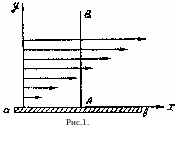 язкостью или внутренним трением называется особое свойство жидкости и газа, заключающееся в том, что при перемещении одной части жидкости или газа относительно другой возникает сила, направленная против скорости этого, относительного движения.

Возникновение этой силы можно объяснить так: пусть жидкость или газ движутся вдоль какой-либо твердой пластины (рис.1) в направлении, указанном стрелкой. Это направление мы примем за Ox, а перпендикулярное ему направление за ось O .

Молекулы жидкости (или газа), непосредственно прилегающие к пластинке, прилипают к ней вследствие сил протяжения, действующих между ними и молекулами материала пластины. Значит, скорость этого слоя окажется равной нулю, скорость молекул следующего слоя уже отлична от нуля, так как тормозящее действие пластины на этот слой меньше. Но скорость молекул этого слоя меньше, чем в слое еще более удаленном. На более удаленные от пластины слои жидкости (или газа) действие самой пластины уже ничтожно мало, но зато большую роль играет взаимодействие между молекулами самой жидкости. Благодаря этому взаимодействию на каждый слой жидкости со стороны нижележащего слоя действует тормозящая сила. В то же время со стороны вышележащего слоя на него действует ускоряющая сила.

Таким образом, оказывается, что всю толщину жидкости (или газа) можно рассматривать как составленную из множества слоев, скорости которых различны и меняются от нуля у самого нижнего слоя до некоторой максимальной скорости у самого верхнего слоя.

Благодаря тепловому движению молекулы жидкости (или газа) переходят из одного слоя в другой, перенося с собой некоторый импульс : молекулы из более медленно движущегося слоя переходят в слой с большей скоростью и, таким образом, уменьшают его импульс, а, значит, и скорость. Наоборот, молекулы из более быстрых слоев, переходя в слой, движущийся с меньшей скоростью, увеличивают импульс, а значит и скорость последнего. В жидкостях, которыми мы в дальнейшем будем заниматься, главную роль играет не тепловое молекулярное движение, а силы взаимодействия между молекулами. Если речь идет о газе, то главной причиной вязкости является тепловое движение молекул газа.

Если мы возьмем какое-либо сечение жидкости AB, перпендикулярное направлению ее движения (см.рис. 1), то вдоль оси Oy скорости слоев жидкости будут увеличиваться по мере удаления от пластины, вдоль которой происходит движение.

Сила F внутреннего трения (или вязкости), как впервые показал Ньютон, пропорциональна площади S соприкосновения слоев жидкости, а также градиенту скорости вдоль оси Oy, т.е. вдоль направления, перпендикулярного движению жидкости. Напомним, что градиент скорости равен изменению скорости на каждой единице длины, т.е. в нашем случае .

Формулу для силы F можно поэтому записать так:

(1).

Здесь η - коэффициент пропорциональности, различный для разных жидкостей. Именно этот коэффициент определяет вязкие свойства данной жидкости. Называется он коэффициентом динамической вязкости или просто вязкостью. Смысл его ясен из формулы (1). Если градиент скорости paвен единице (это значит, что на каждой единице длины вдоль оси скорость изменяется на единицу), и S = 1, то η = F, то есть коэффициент вязкости равен силе, действующей на каждую единицу площади соприкосновения слоев при градиенте скорости (в направлении, перпендикулярном движению) равном единице.

Из уравнения (1) видно, что размерность коэффициента вязкости

.

В системе СИ динамический коэффициент вязкости измеряется в паскаль-секундах (1 Па·с = 1 ).

В системе СГС единица измерения динамического коэффициента вязкости названа в честь французского физика Ж.Л.М. Пуазейля пуазом:

имеет размерность .

Возникновение вязкости у газов обусловлено переносом импульса упорядоченного движения молекул газа из слоя в слой при их тепловом движении. Он определяется, главным образом, силами межмолекулярного взаимодействия. Так как молекулы жидкости расположены на близком расстоянии друг от друга, то силы притяжения между ними значительны, они и обуславливают большую вязкость жидкости. Кроме сил притяжения между молекулами существуют и силы отталкивания, препятствующие сближению молекул. Совместное действие этих сил приводит к тому, что для каждой молекулы существует положение равновесия, около которого она колеблется в течение некоторого времени (~10^-10 с), называемого временем оседлости. По истечении этого времени молекула перемещается в новое положение равновесия на расстояние ~10^-10 м.

Возможность изменения положения молекул приводит к их подвижности и, следовательно, к текучести φ, которая является величиной, обратной вязкости

.

При повышении температуры T энергия колебательного движения молекул возрастает, уменьшается время оседлости и коэффициент вязкости резко падает. Зависимость η от T выражается следующим образом:

(2),

где A – коэффициент, зависящий от рода жидкости,

ρ – плотность жидкости,

k – постоянная Больцмана,

e – основание натуральных логарифмов,

ΔW – энергия активации, т.е. та энергия, которую необходимо сообщить молекуле, чтобы она смогла преодолеть связь с соседними молекулами и переместится в новое положение равновесия.

Из формулы (2) видно, что с ростом температуры жидкости коэффициент вязкости уменьшается по экспоненциальному закону, т.е. очень быстро.