3.2. Принцип относительности классической механики

Предположим, что подвижная система отсчета движется поступательно, равномерно и прямолинейно. При этом угловая скорость и угловое ускорениеподвижной системы координат, а также ускорение ее началаравны нулю. Следовательно, равны нулю переносное, кориолосовоускорения и обе силы инерции,. Теперь уравнение (3.5) примет вид:

. (3.7)

Сравнивая уравнения (3.1) и (3.7), приходим к выводу о том, что в рассматриваемом случае последнее уравнение, определяющее относительное ускорение материальной точки, совпадает с основным уравнением динамики (3.1), определяющим ее абсолютное ускорение. Таким образом, движение материальной точки относительно системы отсчета, движущейся поступательно, равномерно и прямолинейно, происходит так же, как и относительно неподвижной системы отсчета, т.е. подвижная система является инерциальной.

Действительно, если правая часть уравнения (3.7) равна нулю, то из него получим , откуда следует, что точка движется равномерно и прямолинейно, т.е. выполняется 1-й закон динамики. Так как законы динамики одинаковы во всех инерциальных системах отсчета, никакие механические эксперименты, проводимые в инерциальной системе отсчета, не могут обнаружить, находится ли она в покое или движется поступательно, равномерно и прямолинейно. В этом состоит открытый Галилеем принцип относительности классической механики.

3.3. Условия относительного покоя. Сила тяжести

Пусть материальная точка под действием приложенных к ней сил находится в состоянии относительного покоя, т.е. не движется относительно подвижной системы отсчета Oxyz. В этом случае относительная скоростьи относительное ускорениеточки равны нулю, следовательно, равна нулю и кориолисова сила инерции. Уравнение относительного покоя получим из уравнения (3.5)

. (3.8)

Таким образом, если материальная точка находится в состоянии относительного покоя, геометрическая сумма действующих на нее сил и переносной силы инерции равна нулю. Следует отметить, что выполнения условия (3.8) не означает, что после сообщения точке начальной скорости она будет двигаться равномерно и прямолинейно относительно подвижной системы, как это имеет место в инерциальной системе отсчета. Действительно, при появлении относительной скорости, во-первых, возникает кориолисово ускорение и кориолисова сила инерции, во-вторых, может измениться переносное ускорение, зависящее от положения точки в подвижной системе отсчета, что приведет к изменению переносной силы инерции. Таким образом, правая часть уравнения (3.5) будет отлична от нуля, и точка будет иметь относительное ускорение.

Рассмотрим в качестве примера материальную точку М, подвешенную на нити и находящуюся в покое относительно Земли (рис. 3.3). Запишем условие относительного покоя (3.8) и получим

, (3.9)

где – реакция нити;– сила притяжения Земли, направленная к ее центру;– переносная сила инерции, которая вследствие равномерного вращения Земли имеет только центробежную составляющую, направленную от ее оси вращения. Модуль силы инерции

,

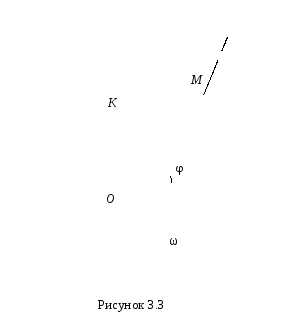
где ρ = МК– радиус географической параллели;R– радиус Земли; ω – угловая скорость вращения Земли; φ – геоцентрическая широта. Силу, равную по модулю и направленную противоположно реакции, называютсилой тяжестии обозначают через. Таким образом, сила тяжести равна геометрической сумме силы притяженияи силы инерции, вызванной вращением Земли:

.

Направление силы тяжести определяет направление вертикали в данной точке земной поверхности, а плоскость, перпендикулярная силе, является горизонтальной.

Сила инерции очень мала по сравнению с силой тяжести, что видно из отношения их модулей

.

Оно максимально на экваторе (1/290) и равно нулю на полюсе. Отклонение линии отвеса от направления радиуса Земли максимально на широте 45⁰и составляет. Таким образом, сила тяжестии по модулю, и по направлению мало отличается от силы притяжения. Ускорение свободного паденияgмаксимально на полюсе (9,83 м/с²) и минимально на экваторе (9,78 м/с²).

Пример.Тело массойmнаходится на гладкой наклонной грани призмы, движущейся по горизонтальной поверхности, как показано на рис. 3.4.

Определить:

1) Каким должно быть ускорение призмы, чтобы тело не двигалось относительно нее?

2) Каково давление тела на призму, если угол наклона равен α?

На тело действуют сила тяжести и нормальная реакциягладкой плоскости. Условно приложим к телу переносную силу инерции, модуль которой, и запишем для полученной системы сил уравнение равновесия

.

Спроецируем его на оси xиyподвижной системы координат:

; (3.10)

. (3.11)

Теперь получим:

из уравнения (3.10)

, откуда;

из уравнения (3.11)