6.4. Дифференциальное уравнение вращательного движения

твердого тела

Рассмотрим тело, вращающееся вокруг неподвижной оси zс угловой скоростью ω. На него действуют система внешних сил () и реакции опор(рис. 6.6). Чтобы исключить из рассмотрения неизвестные реакции, запишем 3-е уравнение системы (6.14):

. (6.21)

Поскольку в соответствии с формулой (6.9), из уравнения (6.21) получим

(6.22)

или

, (6.23)

где φ – угол поворота тела.

Сравнивая последнее уравнение с дифференциальными уравнениями движения центра масс (5.23), применяемыми для описания поступательного движения тела, приходим к выводу об аналогичности структур этих уравнений. Поскольку масса характеризует инертность тела, совершающего поступательное движение, момент инерции является мерой инертности тела, вращающегося вокруг неподвижной оси.

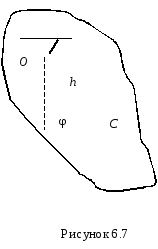Рассмотрим в качестве примера движение под действием силы тяжести физического маятника, т.е. тела, имеющего горизонтальную ось вращения, которая не проходит через центр масс телаС(рис. 6.7). Обозначим черезсилу тяжести физического маятника,– реакцию его оси,h – расстояние от оси вращения до центра масс тела. Совместим осьz с осью вращения тела и запишем дифференциальное уравнение вращательного движения

или

, (6.24)

где – момент инерции физического маятника относительно оси вращения.

Рассмотрим малые колебания, при которых . Уравнение (6.24) примет вид:

или

, (6.25)

где . Полученное уравнение совпадает с уравнением (2.2), описывающим свободные колебания материальной точки в среде без сопротивления. Таким образом, малые свободные колебания физического маятника являются гармоническими

,

где постоянные Аи α определяют из начальных условий, а период этих колебаний находят по формуле

.

Вопросы для самоконтроля

1. Как определить кинетический момент материальной точки и механической системы?

2. Чему равен кинетический момент твердого тела относительно неподвижной оси вращения?

3. Как сформулировать теоремы об изменении кинетического момента материальной точки и механической системы?

4. Как сформулировать закон сохранения кинетического момента механической системы?

5. Как записать дифференциальное уравнение вращательного движения твердого тела?

Лекция 7.Теорема об изменении кинетической энергии

7.1. Кинетическая энергия материальной точки

и механической системы

Рассмотренные в лекциях 5 и 6 меры механического движения – количество движения и кинетический момент – не описывают движение системы, происходящее под действием внутренних сил. Приведем в качестве примера систему, состоящую из двух одинаковых шаров, соединенных пружиной (рис. 7.1).

Сожмем пружину и отпустим шары без начальной скорости, поместив их на гладкую горизонтальную плоскость. Под действием внутренних сил (сил упругости пружины) шары будут совершать колебательное движение, причем в любой момент времени их скорости будут равны по величине и противоположны по направлению . Количество движения и кинетический момент этой системы относительно произвольной неподвижной точкиО тождественно равны нулю и не отражают движение системы:

;

.

Этого недостатка не имеет рассматриваемая в данной лекции динамическая характеристика – кинетическая энергия.

Кинетическая энергия материальной точки – это скалярная мера механического движения, равная половине произведения массы точки на квадрат ее скорости:

. (7.1)

Единица измерения кинетической энергии в системе СИ – 1 Дж.

Кинетическая энергия механической системы – это сумма кинетических энергий всех материальных точек, образующих систему:

. (7.2)

Кинетическая энергия является неотрицательной величиной, она равна нулю только в том случае, если неподвижны все точки системы. Однако и кинетическая энергия не является универсальной мерой движения, так как, будучи величиной скалярной, не отражает направление движения.