Вопросы для самоконтроля

1. Какие существуют меры механического движения и меры действия силы?

2. Как определить количество движения материальной точки и механической системы?

3. Как определить элементарный импульс силы и импульс силы за конечный интервал времени?

4. Как сформулировать теоремы об изменении количества движения материальной точки и механической системы?

5. Как сформулировать теоремы Эйлера и о движении центра масс механической системы?

Лекция 6.Теорема об изменении кинетического момента

6.1. Кинетический момент материальной точки и

механической системы

Кинетический момент материальной точкиМ относительно неподвижного центраО – это величина, равная векторному произведению радиус-вектора этой точки, проведенного из центраО, на ее количество движения (рис. 6.1):

. (6.1)

В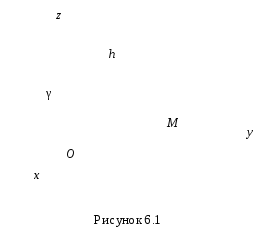екторное произведение в правой части (6.1) представляет собой момент вектораотносительно центраО, отсюда 2-е название вектора–момент количества движения,

. (6.2)

Вектор направлен перпендикулярно плоскости, проходящей через вектори центрО, в ту сторону, откуда векторвиден направленным против часовой стрелки относительно этого центра. Его модуль:

, (6.3)

где h– плечо вектораотносительно центраО.

Единица измерения кинетического момента в системе СИ – 1 кг·м²/с.

Кинетический момент материальной точки относительно неподвижной оси равен проекции на эту ось кинетического момента точки относительно любого центра, выбранного на данной оси (см. рис. 6.1):

. (6.4)

Определение кинетического момента относительно оси аналогично вычислению соответствующего момента силы – спроецируем вектор на плоскость, перпендикулярную оси, и определим алгебраический момент проекции относительно точки пересечения оси и плоскости (см. рис. 6.1):

. (6.5)

Кинетический момент , если, глядя с положительного направления осиz, видим векторнаправленным против часовой стрелки относительно центраО.

Кинетический момент (главный момент количеств движения) механической системы относительно неподвижного центраО равен сумме кинетических моментов всех материальных точек системы относительно этого центра:

. (6.6)

Аналогично определяют кинетический момент системы относительно неподвижной оси:

. (6.7)

Определим кинетический момент твердого тела относительно неподвижной оси вращенияz(рис. 6.2). Обозначив черезрасстояние от точкидо оси вращения, вычислим кинетический момент точки относительно осиz

,

а также кинетический момент тела

. (6.8)

По определению (см. подраздел 4.3), полученная сумма является моментом инерции тела относительно оси z:, поэтому из выражения (6.8) получим

. (6.9)

Таким образом, кинетический момент твердого тела относительно оси вращения равен произведению момента инерции тела относительно данной оси на проекцию его угловой скорости на ту же ось.