Text three higher dimensions

One advantage of treating geometrical problems with analytic methods is that it becomes easier to generalize concepts beyond those dealing with three dimensions.  In other words, the methods of Analytic Geometry make it easier to study geometric objects for which our power of visualization fails.

To illustrate this let us show how the notion of a distance can be generalized from one and two dimensions to three, four,  five and even higher dimensions.  One knows that the distance between(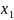 ,  ), and(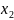 ,  ), namely,  the distance between two points in a plane is d= 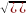 In order to generalize this formula to three dimension we have only to consider a coordinate system consisting of three mutually perpendicular axes.  With the use of this system we can locate any point in space by starting at the origin, going a certain distance to the right or left, then to the front or back,  and finally,  a certain distance up or down.  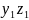With perpendicular axes like these we can identify each point with three coordinates x, y and z,  and one can show that the distance between points ( ,  ),   and( , 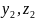 )  is d=  .As in the two-dimensional case,  the derivation of this formula is based on the Pythagorean theorem.  If one wants to express these two distance formulas in words, one can say that “the distance between two points is given by the square root of the sum of the squares of the differences of the respective coordinates”.  Since this rule applies to one, two and three dimensions, it is tempting to let it apply also in the case where there are more than three.

  In order to make such a generalization it will be necessary to explain first what mathematician means when he speaks of four-dimensional, five-dimensional,or n-dimensional space.  Evidently, the word “space” can no longer be interpreted in its colloquial sense standing for “physical space” or “the space we live in”. Taking this term in its colloquial sense one can hardly go beyond the customary three dimensions of “left and right”, “front and back”, and “up and down”. Indeed, when mathematical talks about a space he is referring to a collection of mathematical objects which (for the sake of convenience) may bereferred to as points. He then defines the dimension of such a space as the number of coordinates needed to determine each point.

  A line or a curve constitutes a one-dimensional space since each point can be identified with one real number.  Similarly, a plane or a surface constitutes a two-dimensional space since each point can be identified with two real numbers,  namely,  its two coordinates.  Since three numbers are needed to locate a point in ordinary space one says that these points constitute three-dimensional space.  So far the mathematical concept of a dimension agrees with the intuitive notion which one ordinarily associates with this term.  However,  the analogy breaks down the moment one says that a collection of points constitutes a four-dimensional space because four numbers are needed to determine each point or if one says that a collection of points constitues an n-dimensional space because n numbers are needed to determine each point.

It must be understood, therefore, that when a mathematician speaks of a four-dimensional space, he does not refer to some mysterious generalization of the intuitive notion of a three-dimensional space.  He refers to a set of mathematical objects which are individually determined by means of four numbers.  To give an example of such a four-dimensional space, let us consider the position of an airplane at two different times:  at 1:15 p.m. and 1:17 p.m.  One says that the position of the airplane is in each case given by a point in three-dimensional space.  Although the position of airplane is given by three coordinates x,  y,  z,  it cannot be found unless one also knows the time,  i.e.,  unless one knows a fourth variable t.  In other words, to specify the location of the airplane one has to give four numbersx, y, z, t.It is in this sense, that one says that the location of the airplane is a point in a four-dimensional space.  Naturally, it will be unreasonable to expect that one can visualize this in the same way in which one can visualize a point in one-, two-, or three-dimensional space.  As a second example of a higher dimensional space let consider rolls of die which yielded the numbers 3, 6, 1, 2, 5. When taken individually, those rolls of a die are given as single numbers,  i.e.,  they are points in a one-dimensional space,  when taken together they can be looked upon as a single point in a five-dimensional space.  In other words, the experiment as a whole is characterized by five numbers, and is therefore a point in a five dimensional space.  In the given example the rolls of the die correspond to the point(3,  6.  1,  2,  5).  If the rolls are all 2's,  they will correspond to the point(2,  2,  2,  2,  2).

  Statisticians often refer to a sample of five measurements as a point in a five-dimensional sample space, and more generally, they refer to a sample of n measurements as a point in an n-dimensional sample space.  This is just another way of saying that the sample as a whole consisted n numbers.  Physicists often consider systems of molecules in which the position of each molecule is determined by three coordinates x, y,z.  If a gas consists of 1,000,000 molecules we shall need 3,000,000 numbers to describe the gas as a whole and we therefore refer to the state of this gas as a point in a 3,000,000-dimensional space.  If we also want to describe the motion of each particle, three more numbers will be needed for each molecule and the state of the gas will be a point in a 6,000,000- dimensional space.

Let us now return to the problem which originally motivated this brief excursion into higher dimensions,  namely the problem of generalizing the formula which measures the distance between two given points. 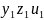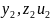Applying the rule that distance between two points is the square root of the sum of the squares of the differences of the respecive coordinates to four-dimensions, one can write the distance between points( ,  , ),  and( ,  , )  as a formula d=  .  It is important to note that this formula actually difines what one means by the distance between two points in a four-dimensional space.  Proceeding in the same way, one can also define the distance between two points in a five-dimensional space asd=  and if one introduces a suitable notation one will be able similarly to define the distance between two points in n-dimensional space.  In the same way, in which we generalized the distance formula we are able to generalize many of the other formulas and equations of Analytic Geometry.  For example, where in two dimensions ax+bx+c=0is the equation of a line,  we shall say that in three dimensions ax+ by+ cz+ d=0 is the equation of a plane,  and that in four dimensions ax+by+cz+du+e=0is the equation of a hyperplane.

  In Analytic Geometry one insists that it takes two numbers to locate point in the plane,  i.e.,  it takes two coordinates to identify a point in a two-dimensional space.  This is correct only as long as we restrict ourselves to real numbers, there is a way in which one can identify each point of plane by means of a single complex number.  This is done simply by identifying the point whose coordinates are (x, y) with, the complex number x+iy.  This means that one can identify the points(l,4), (-2,5) and(3, -7)  with the complex numbers 1+ 4i, -2+5i,  3-7iand that can viceversa plot the points2+3i and 4-2i. (They are the points whose coordinates are (2,3)  and (4-2).)  One can thus identify the x and y-coordinates of a point with the real and the imaginary parts of a complex number and represent each point by means of a unique complex number. Incidentally, this provides a “concrete” interpretation of the complex numbers.  Complex numbers, thus, represent the points of a plan.