8. Ряды Тейлора и Маклорена.

Рядом Тейлора для функции называется степенной ряд

.

(18)

При этом говорят, что ряд Тейлора построен для в точке .

Остаток ряда Тейлора может быть записан в форме Лагранжа:

, .

Если функция бесконечно дифференцируема в некоторой области и при этом в этой области выполняется условие

,

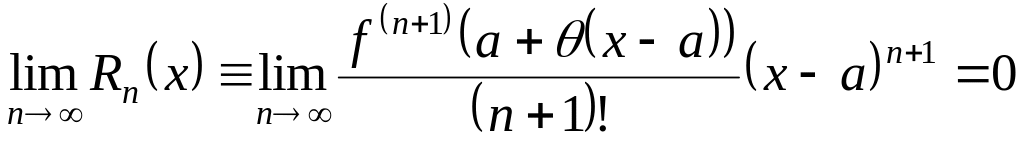то ряд (17) в данной области сходится к функции , т.е. справедливо равенство

.

Частный случай ряда Тейлора при называется рядом Маклорена. Остаток ряда Маклорена в форме Лагранжа имеет вид:

, ,

а разложение функции в ряд Маклорена, при условии , выглядит следующим образом:

.

Если , то ряд Тейлора (Маклорена), даже если он сходится, имеет сумму, отличную от .

Ряды Маклорена для некоторых элементарных функций, представленные ниже вместе с их областями сходимости, полезно запомнить для их применения при разложении других, более сложных функций.

.

.

.

.

Последний ряд называется биномиальным, т.к. функция, для которой построен этот ряд, представляет собой бином (двучлен) произвольной степени . Гарантированная область сходимости биномиального ряда указана для любых значений ; для некоторых значений она может быть расширена в ту или другую сторону (или в обе) включением в нее границы интервала.

Частные случаи биномиального ряда выглядят следующим образом:

.

.

Из первого частного случая могут быть получены ряды еще для двух часто встречающихся в практических задачах функций:

;

.

9. Применение степенных рядов для вычисления функций и определенных интегралов.

Для вычисления значения функции при данном значении аргумента можно воспользоваться разложением этой функции в степенной ряд. В частности, удобно воспользоваться приведенными в предыдущем пункте разложениями в ряд Маклорена функций . Если значение аргумента принадлежит области сходимости, то после разложения функции в ряд и подстановки искомое значение функции представляет собой сумму числового ряда. Поскольку полную сумму ряда, представляющую собой точное значение функции, найти, как правило, затруднительно, то в этом ряде сохраняется такое количество первых членов, которое гарантирует необходимую в данном конкретном случае точность. Точность вычислений задается обычно одной значащей цифрой в каком-либо разряде. Так, запись означает, что точное значение величины находится в пределах от 5,39 до 5,43. Это можно записать следующим образом: . Другими словами, заданная точность - это та погрешность, в пределах которой приближенное значение может отличаться от точного.

Для приближенного вычисления определенного интеграла нужно разложить в степенной ряд подынтегральную функцию, проинтегрировать степенной ряд почленно и сохранить в ряде достаточное для обеспечения заданной точности количество его первых членов; при этом область интегрирования не должна выходить за рамки области сходимости ряда.