24. Поняття протилежної події. Приклади

Дві події називаються протилежними (opposite), якщо вони несумісні і складають повну групу.

Сума ймовірностей протилежних подій дорівнює одиниці:

.

Це випливає з того, що в іспиті обов’язково відбудеться або подія А або подія , і на основі теореми про суму подій та їх ймовірностей одержимо:

.

Якщо випадкові події А1, А2, А3, ..., Аn утворюють повну групу несумісних подій і ‑ їх ймовірності, то сума ймовірностей дорівнюватиме одиниці:

=1.

Для довільної події А імовірність протилежної події обчислюється за формулою .

Приклад. (Із “схеми урн”) В урні 10 червоних, 5 синіх і 15 білих кульок. Всього 30 кульок. Витягується 1 кулька. Знайти ймовірність появи кольорової кульки.

Розв’язання.

Поява кольорової кульки означає появу або червоної, або синьої кульки. Подія А ‑ поява червоної кульки, В ‑ поява синьої кульки, С ‑ поява кольорової кульки С=А+В, Р(С)=Р(А)+Р(В) події А і В несумісні. Р(А)=10/30=1/3, Р(В)=5/30=1/6; Р(С)=1/3+1/6=3/6=0,5 або Р(С)=(10+5)/30=0,5.

25. Теорема додавання ймовірностей.

Нехай в досліді можуть мати місце: випадкова подія А1 з імовірністю Р(А1) і подія А2 з імовірністю Р(А2). Події А1 і А2 несумісні. Тоді імовірність суми подій, тобто того, що відбудеться або подія А1, або А2, дорівнює сумі ймовірностей цих подій і обчислюється за формулою: Р(А1+А2 )=Р(А1)+Р(А2).

26. Класичне означення ймовірностей подій.

Імовірність події — це відношення числа сприятливих випадків до числа усіх можливих випадків, коли ніщо не вказує на те, що будь-який з цих випадків має відбуватися частіше, ніж будь-який інший, що робить їх для нас рівноможливими.

27. Теорема множення ймовірностей.

Імовірність добутку двох подій дорівнює добутку ймовірності однієї з них на умовну ймовірність іншої, обчислену за умови, що перша мала місце .

28. Формула повної ймовірності.

Формула повної ймовірності дозволяє обчислити ймовірність деякої події через умовні ймовірності цієї події в припущенні якихось гіпотез, а також ймовірностей цих гіпотез.

29. Поняття умовної ймовірності.

Якщо подія А відбувається у випробувані, яке обмежене додатковими умовами здійснення події В, то міра можливості події А визначається умовною ймовірністю P(B | B). Отже, умовною ймовірністю Р(A | B) називається ймовірність події А, обчислена за умови, що подія В вже відбулася.

Умовна ймовірність має сенс для залежних подій. Для незалежних подій А і В умовна ймовірність перетворюється на звичайну:

Р(A | B) = Р(А), або Р(B | А) = Р(B).

30. Ймовірність протилежної події.

Для будь-якої події А ймовірність протилежної події Р(А) = 1 - Р(А). Сума ймовірностей протилежних подій дорівнює одиниці: Р( А) + Р( А) = 1.

31. Схема повторення дослідів. Формула Бернулі.

Проводяться n дослідів, у кожному з яких може настати певна подія («успіх») з ймовірністю p (або не настати — «неуспіх» — q = 1 — p). Задача — знайти ймовірність отримати m успіхів у досліді. Розв'язок:

Формула Бернуллі:

33. Локальна теорема Лапласа При великих n(соті) і малих p – має місце формула Лапласа Pn(K)= (х) (х)- диф. Функція Лапласа(Значення шукають в таблицях)

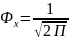
34.Інтегральна теорема Лапласа В умовах схеми дослідів ставиться задача про знаходження імовірності того, що в n подія A відбудеться від до Д≤ ≤ ≤n ( ) - непарна функція. Значення функції задаються таблицею для додатніх х, а – для відємних При х≥5 ;