Глава 1 Элементы теории вероятностей

1. Основные понятия комбинаторики

В разделе математики, который называется комбинаторикой, решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. Например, возьмем 10 различных цифр 0, 1, 2, 3, …, 9 и составим из них комбинации различных чисел: 345; 23; 32; 5036; 1248; … . Видим, что некоторые из таких комбинаций отличаются только:

- порядком цифр (32; 23);

- входящими в них цифрами (5036; 1248);

- числом цифр (345; 23).

Таким образом, полученные комбинации удовлетворяют различным условиям. В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания. Рассмотрим их отдельно. Предварительно познакомимся с понятием факториала.

2. Понятие факториала.

Определение. Произведение всех натуральных чисел от 1 до n включительно называют n-факториалом и пишут

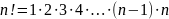
Считают, что 1!=1, 0!=1.

2. Перестановки

Пусть даны три буквы A, B, C. Составим всевозможные комбинации из этих букв.

Определение. Комбинации из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками.

Перестановки обозначаются символом P_n, где n – число элементов, входящих в каждую перестановку.

Число перестановок можно вычислить по формуле 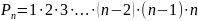или с помощью факториала.

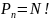
2. Размещения

Пусть имеются четыре буквы A, B, C, D. Составим комбинации только из двух букв.

Определение. Комбинации из m элементов по n элементов, которые отличаются друг от друга или самими элементами, или порядком элементов, называются размещениями.

Размещения обозначаются символом 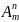, где m – число всех имеющихся элементов, n – число элементов в каждой комбинации, (m≥n), и вычисляются по формуле:

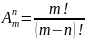(2)

2. Сочетания

Из четырех различных букв A, B, C, D составить комбинации, которые отличаются друг от друга хотя бы одним элементом:

Определение.

Сочетаниями называются все комбинации из m элементов по n, которые отличаются друг от друга по крайней мере хотя бы одним элементом, (n≤m).

Сочетания обозначаются символом 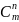и вычисляются по формуле

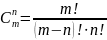
Примеры:

1. Вычислить: 3!; 7!−5!; .

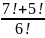2. Упростить: ; .

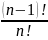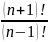3. Сколько двузначных чисел можно составить из пяти цифр 1, 2, 3, 4, 5 при условии, что ни одна из них не повторяется.

4. Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек?

5. Сколькими способами можно составить школьное расписание из шести предметов?

6. Сколькими способами можно выбрать четырех участников из 15 членов сборной и расставить их для эстафеты 800+400+200+100 метров?

7. Сколько вариантов распределения трёх путёвок в санаторий различного профиля можно составить для пяти претендентов?

8. Сколькими способами можно выбрать из 25 учащихся одного класса 5 человек для участия в интеллектуальном марафоне?

9. Сколькими способами могут быть выделены три призовых места среди 1 соревнующихся?

10. Сколькими способами можно заполнить билет «5 из 36»?

11. Сколько различных «слов» можно получить, переставляя буквы в слове СОЛНЦЕ?

12. Сколькими способами можно выбрать две детали из ящика, содержащий 10 деталей?

13. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?