
- •Теоретический минимум Основные понятия эконометрики
- •Элементы корреляционно-регрессионного анализа Основные понятия корреляционного анализа
- •Понятие о регрессионной модели
- •Задачи корреляционно-регрессионного анализа
- •Линейная парная регрессия
- •Метод наименьших квадратов
- •Модель множественной регрессии
- •Нелинейная эмпирическая регрессия
- •Эконометрический анализ при нарушении классических предположений. Временные ряды Основные проблемы при нарушении классических предположений
- •Мультиколлинеарность
- •Автокорреляция
- •Гетероскедастичность
- •Временные ряды
- •Системы одновременных уравнений
Автокорреляция
Автокорреляция (последовательная корреляция) определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные данные).
Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании данных временных рядов.
Методы определения автокорреляции:
Графический метод. По оси абсцисс откладываются либо время (момент) получения статистических данных, либо порядковый номер наблюдения, а по оси ординат – отклонения (либо оценки отклонений). По графику предполагают, имеются ли определенные связи между отклонениями, т.е. автокорреляция. Отсутствие зависимости, скорее всего, свидетельствует об отсутствии автокорреляции. Можно также график дополнить графиком зависимости et от et-1.
Тест Дарбина-Уотсона.
Гетероскедастичность
Одной из ключевых предпосылок МНК является условие постоянства дисперсий случайных отклонений. Выполнимость данной предпосылки называется гомоскедастичностъю. Невыполнимость данной предпосылки называется гетероскедастичностъю (непостоянством дисперсий отклонений). Проблема гетероскедастичности характерна для перекрестных данных и довольно редко встречается при рассмотрении временных рядов. Не существует однозначного метода определения гетероскедастичности. Однако для проверки разработано много тестов и критериев. Наиболее популярные и наглядные: графический анализ отклонений, тест ранговой корреляции Спирмена, тест Парка, тест Глейзера, тест Голдфелда—Квандта.
Использование графического представления отклонений позволяет определиться с наличием гетероскедастичности. В этом случае по оси абсцисс откладываются значения объясняющей переменной X (либо линейной комбинации объясняющих переменных), а по оси ординат либо отклонения, либо их квадраты.
Если все отклонения находятся внутри полосы постоянной ширины, параллельной оси абсцисс, то это говорит о независимости дисперсий от значений переменной X и их постоянстве, т.е. в этом случае выполняются условия гомоскедастичности.
Если наблюдаются некоторые систематические изменения в соотношениях между значениями переменной X и квадратами отклонений (линейная, квадратичная, гиперболическая и др. зависимости), то такие ситуации отражают большую вероятность наличия гетероскедастичности для рассматриваемых статистических данных.
Временные ряды
Для характеристики и анализа различных социально-экономических явлений за определенный период применяют показатели и методы, характеризующие эти процессы во времени (динамике). Под временным рядом в экономике понимается последовательность наблюдений некоторого признака (случайной величины) Y в последовательные моменты времени. Отдельные наблюдения называются уровнями ряда, которые будем обозначать уt (t= 1,2,..., n), где п – число уровней. Последовательно расположенные во времени числовые показатели характеризуют уровень состояния и изменения явления или процесса.
Классификация временных рядов:
В зависимости от показателя времени, временные ряды бывают моментные (на определенную дату) и интервальные (за определенный период).
По форме представления уровни во временном ряду могут быть представлены абсолютными, средними и относительными величинами.
По расстоянию между уровнями временные ряды подразделяются на ряды с равноотстоящими и неравноотстоящими уровнями по времени. В равноотстоящих рядах даты регистрации периода следуют друг за другом с равными интервалами, в неравноотстоящих равные интервалы не соблюдаются.
По содержанию показатели временных рядов подразделяют на состоящие из частных показателей и агрегированных показателей. Частные показатели характеризуют явления изолированно, односторонне (например, динамика показателей среднесуточного объема потребленной воды); агрегированные показатели являются производными от частных показателей и характеризуют изучаемое явление комплексно (например, динамика показателей экономической конъюнктуры).
В общем виде при исследовании экономического временного ряда уt выделяются несколько составляющих

где
 — тренд, плавно
меняющаяся компонента, описывающая
чистое влияние долговременных факторов,
т. е. длительную тенденцию изменения
признака (например, рост населения,
экономическое развитие, изменение
структуры потребления и т. п.);
— тренд, плавно
меняющаяся компонента, описывающая
чистое влияние долговременных факторов,
т. е. длительную тенденцию изменения
признака (например, рост населения,
экономическое развитие, изменение
структуры потребления и т. п.);
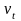 ,
— сезонная
компонента, отражающая
повторяемость экономических процессов
в течение не очень длительного периода
(года, иногда месяца, недели и т. д.,
например, объем продаж товаров или
перевозок пассажиров в различные времена
года);
,
— сезонная
компонента, отражающая
повторяемость экономических процессов
в течение не очень длительного периода
(года, иногда месяца, недели и т. д.,
например, объем продаж товаров или
перевозок пассажиров в различные времена
года);
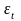 — случайная
компонента, отражающая
влияние не поддающихся учету и
регистрации случайных факторов.
— случайная
компонента, отражающая
влияние не поддающихся учету и
регистрации случайных факторов.
Следует обратить внимание на то, что в отличие от первые составляющие , являются закономерными, неслучайными.
Модели, в которых временной ряд представлен как сумма перечисленных компонент называются аддитивными; как произведение – мультипликативными моделями временного ряда.
Аддитивная модель имеет вид .
Мультипликативная модель
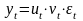 .
Такую модель применяют в случае, если
происходят существенные сезонные
изменения
.
Такую модель применяют в случае, если
происходят существенные сезонные
изменения
Среди наиболее распространенных методов анализа временных рядов выделим корреляционный анализ, модели авторегрессии и скользящей средней.
Важное значение
в анализе временных рядов имеют
стационарные временные ряды, вероятностные
свойства которых не изменяются во
времени. Стационарные временные ряды
применяются, в частности, при описании
случайных составляющих анализируемых
рядов. Временной ряд
 (t=
1,2,..., n)
называется стационарным,
если совместное
распределение вероятностей п
наблюдений
(t=
1,2,..., n)
называется стационарным,
если совместное
распределение вероятностей п
наблюдений
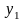 ,
,
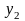 ,...,
,...,
 такое же, как и п
наблюдений
такое же, как и п
наблюдений
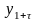 ,
,
 ,...,
,...,
 при любых
,
при любых
,
 и
и
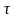 .
Иначе говоря, свойства стационарных
рядов
не зависят от момента
,
т. е. закон
распределения и его числовые характеристики
не зависят от
.
Поэтому
математическое ожидание и среднее
квадратическое отклонение могут быть
оценены по наблюдениям
(t=
1,2,..., n)
по формулам
.
Иначе говоря, свойства стационарных
рядов
не зависят от момента
,
т. е. закон
распределения и его числовые характеристики
не зависят от
.
Поэтому
математическое ожидание и среднее
квадратическое отклонение могут быть
оценены по наблюдениям
(t=
1,2,..., n)
по формулам
|
|
Степень тесноты связи между последовательностями наблюдений временного ряда , ,..., и , ,..., (сдвинутых относительно друг друга на единиц, или, как говорят, с лагом ) может быть определена с помощью коэффициента корреляции
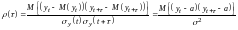 ,
,
ибо
 ,
,
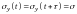 .
.
Так как коэффициент
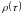 измеряет
корреляцию между членами одного и того
же ряда, его называют коэффициентом
автокорреляции, а зависимость
– автокорреляционной функцией.
В силу стационарности временного ряда
измеряет
корреляцию между членами одного и того
же ряда, его называют коэффициентом
автокорреляции, а зависимость
– автокорреляционной функцией.
В силу стационарности временного ряда
 ,
(
,
(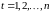 )
автокорреляционная функция
зависит только от лага
)
автокорреляционная функция
зависит только от лага
 ,
причем
,
причем
 .
.
Статистической оценкой
является выборочный коэффициент
автокорреляции
 ,
определяемый по формуле коэффициента
корреляции:
,
определяемый по формуле коэффициента
корреляции:

Функцию
называют выборочной автокорреляционной
функцией, а ее график – коррелограммой.
При расчете
следует помнить, что с увеличением
число
 пар наблюдений
,
пар наблюдений
,
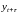 уменьшается, поэтому лаг
должен быть таким, чтобы число
было достаточным для определения
.
Обычно ориентируются на соотношение
уменьшается, поэтому лаг
должен быть таким, чтобы число
было достаточным для определения
.
Обычно ориентируются на соотношение
 .
.
Аналитическое выравнивание временного ряда
Одной из важнейших задач исследования
экономического временного ряда является
выявление основной тенденции изучаемого
процесса, выраженной неслучайной
составляющей
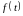 (тренда либо тренда с циклической и
(или) сезонной компонентой). Тренд
– это устойчивая тенденция во временном
ряду более или менее свободная от
случайных колебаний. На практике чаще
всего используют следующие типы временных
рядов: линейный, параболический,
экспоненциальный и др.
(тренда либо тренда с циклической и
(или) сезонной компонентой). Тренд
– это устойчивая тенденция во временном
ряду более или менее свободная от
случайных колебаний. На практике чаще
всего используют следующие типы временных
рядов: линейный, параболический,
экспоненциальный и др.
Для определения параметров функции
тренда
чаще всего используется метод наименьших
квадратов. Значения временного ряда
рассматриваются как зависимая переменная,
а время
– как объясняющая:
 ,
где
,
где
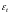 – возмущения, удовлетворяющие основным
предпосылкам регрессионного анализа.
– возмущения, удовлетворяющие основным
предпосылкам регрессионного анализа.
Согласно МНК параметры прямой
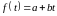 находят из системы нормальных уравнений:
находят из системы нормальных уравнений:

Линейный тип тренда подходит для отображения тенденции примерно равномерного изменения уровней: равных в среднем величин абсолютного прироста или абсолютного сокращения уровней за равные промежутки времени.

 ,
,
 .
.