7. Понятие о фигуре Земли. Геоид. Общий земной эллипсоид.

Изучение формы и размеров Земли включает решение двух задач. Это - установление некоторой сглаженной, обобщенной, теоретической фигуры Земли и определение отклонений от нее фактической физической поверхности.

Учитывая, что поверхность океанов и морей составляет 71% поверхности Земли, а поверхность суши - только 29%, за теоретическую фигуру Земли принято тело, ограниченное поверхностью океанов в их спокойном состоянии, продолженной и под материками, и называемое геоидом.

Поверхность, в каждой своей точке перпендикулярная к отвесной линии (направлению силы тяжести), называется уровенной поверхностью. Из множества уровенных поверхностей одна совпадает с поверхностью геоида.

Из-за неравномерности распределения масс в земной коре геоид имеет неправильную геометрическую форму, и его поверхность нельзя выразить математически, что необходимо для решения геодезических задач. При решении геодезических задач геоид заменяют близкими к нему геометрически правильными поверхностями.

Так, для приближенных вычислений Землю принимают за шар с радиусом 6371 км.

Ближе к форме геоида подходит эллипсоид – фигура, получаемая вращением эллипса (рис. 2.1) вокруг его малой оси. Размеры земного эллипсоида характеризуют следующими основными параметрами: a - большая полуось, b - малая полуось, a - полярное сжатие и e – первый эксцентриситет меридианного эллипса, где  и  

Р ис. 2.1. Меридианный эллипс: Р_с – северный полюс; Рю – южный полюс  

Различают общеземной эллипсоид и референц-эллипсоид.

Центр общеземного эллипсоида помещают в центре масс Земли, ось вращения совмещают со средней осью вращения Земли, а размеры принимают такие, чтобы обеспечить наибольшую близость поверхности эллипсоида к поверхности геоида. Общеземной эллипсоид используют при решении глобальных геодезических задач, и в частности, при обработке спутниковых измерений. В настоящее время широко пользуются двумя общеземными эллипсоидами: ПЗ-90 (Параметры Земли 1990 г, Россия) и WGS-84 (Мировая геодезическая система 1984 г, США). Эллипсоид вращения с малым сжатием называется сфероидом.

8. Поверхности относимости. Референц-эллипсоид.

Поверхность, которая соответствует принятой модели, называется поверхностью относимости. Т.е. реальная физическая поверхность Земли первоначально отображается на поверхность относимости.

В некоторых странах или группе стран во время обработки геодезических измерений используют эллипсоиды с параметрами, полученными по результатам геодезических работ на территории данной страны или нескольких стран. Такие «рабочие» эллипсоиды называются местными эллипсоидами или референц-эллипсоидами. Референц-эллипсоид можно рассматривать как эллипсоид, который наилучшим образом подходит только для некоторой части поверхности Земли.

В Украине, как и в России, а также в бывшем СССР, в качестве отсчетного эллипсоида используется референц-эллипсоид Красовского, который характеризуется следующими параметрами:

Д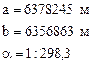 анный эллипсоид был принят в качестве рабочего в бывшем СССР в 1946 году.

Поскольку полярное сжатие референц-эллипсоида очень маленькое, то при решении многих задач за фигуру Земли принимают сферу, которая равна по объему земному эллипсоиду. Для референц-эллипсоида Красовского радиус такой сферы составляет 6371,11 км.