
- •Предмет геодезии
- •2. Задачи геодезии
- •3. Дисциплины, составляющие науку геодезию
- •4. Связь геодезии с другими науками
- •5. Роль геодезии в народном хозяйстве и обороне страны
- •7. Понятие о фигуре Земли. Геоид. Общий земной эллипсоид.
- •8. Поверхности относимости. Референц-эллипсоид.
- •9. Параметры размеров Земли.
- •10. Метод проекций в геодезии
- •13. Элементы объектов, подлежащие измерению на местности
- •14.Понятие о системах проекций
- •15. Масштаб топографической карты. Точность масштаба
- •16. Основные точки, линии и плоскости на геометрической поверхности Земли.
- •17. Система географических координат. Геодезические координаты.
- •18. Система плоских прямоугольных координат.
- •19. Система полярных координат.
- •20. Зональная система прямоугольных координат. Координатная сетка.
- •21. Система высот.
- •22. Ориентирование направлений. Ориентирующие углы.
- •23. Истинный азимут. Сближение меридианов.
- •24. Магнитный азимут. Магнитное склонение. Буссоль.
- •25. Дирекционный угол. Сближение меридианов в проекции Гаусса-Крюгера.
- •27. Прямая геодезическая задача.
- •28. Обратная геодезическая задача.
- •34. Средняя квадратическая ошибка функций измеренных аргументов
- •35. Средняя квадратическая ошибка среднего арифметического
- •3 6. Обработка ряда равноточных измерений
- •3 7. Назначение измерений горизонтальных и вертикальных углов.
- •38. Горизонтальный угол и принцип его измерения.
- •39. Приборы для измерения горизонтальных углов.
- •40. Теодолит, его устройство и назначение основных частей.
- •41. Основные оси и плоскости теодолита.
- •42. Геометрические условия теодолита.
- •43. Порядок поверок и юстировки теодолита.
- •44. Классификация теодолитов по гост.
- •45. Характеристика и устройство теодолитов типа т30 и т5.
- •46. Способы измерения горизонтальных углов.
- •47. Вертикальный угол и принцип его измерения.
- •49. Место нуля вертикального круга.
- •50. Геометрические условия вертикального круга. Поверка и юстировка вертикального круга.
- •51. Измерение вертикальных углов. Формулы для вычисления места нуля и вертикального угла.
- •59. Вычисление длин линий. Приведение длин линий, измеренных мерной лентой к горизонту.
- •60. Порядок измерения расстояний нитяным дальномером. Вычисление расстояний.
- •53. Назначение линейных измерений и их классификация
- •54. Горизонтальное проложение длины линии.
- •56. Непосредственные измерения линий. Мерные приборы
- •57. Мерная лента. Рулетки. Компарирование мерных приборов.
- •58. Порядок измерений линий мерной лентой. Вешение линий
- •59. Вычисление длин линий. Приведение длин линий, измеренных мерной лентой к горизонту
- •60. Порядок измерения расстояний нитяным дальномером. Вычисление расстояний.
- •61. Приведение длин линий, измеренных нитяным дальномером к горизонту.
34. Средняя квадратическая ошибка функций измеренных аргументов
В практике измерений
возможны случаи, когда искомая величина
является функцией непосредственно
измеренных величин (произведением
измеренной величины на постоянный
коэффициент, суммой или разностью,
произведением или частным от деления
двух или нескольких измеренных величин,
линейной функцией или функцией общего
вида). Например, P=πr^2
где P-радиус окружности
(измеренный аргумент) π-const.
В общем случае имеем функции: U=f(x,y,z,…,w)
(39), где x,y,z,…,w
– непосредственно измеренные
аргументы. На основании свойств случайных
ошибок можно записать
 ,
где dU- бесконечно
малая ошибка функции (её полный
дифференциал); dx,dy,…,dw-
бесконечно малые ошибки аргументов
(их дифференциал);
,
где dU- бесконечно
малая ошибка функции (её полный
дифференциал); dx,dy,…,dw-
бесконечно малые ошибки аргументов
(их дифференциал); ;
; ;
; -
частные производные от функции f
по каждому из аргументов – постоянные
величины.
-
частные производные от функции f
по каждому из аргументов – постоянные
величины.
Переходят от
дифференциалов dU,dx,dy,dz,…,dw
к элементарным неизбежным ошибкам
ΔU,
Δx,
Δy,…,
Δw,на
основании формулы Гаусса имеем (см29)
 (40), где
(40), где
 -
суть квадраты коэффициентов;
-
суть квадраты коэффициентов;
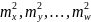 – квадраты средних квадратических
ошибок аргументов. В выражении (40)
отброшены удвоенные произведения
– квадраты средних квадратических
ошибок аргументов. В выражении (40)
отброшены удвоенные произведения
 и т.д.
и т.д.
На основании третьего
свойства случайных ошибок удвоенные
произведения являются величинами
ничтожно малыми, т.к. Δx,
Δy
и т.д. имеют
знаки и (+), и (-) и будут неизбежно
компенсироваться, а при делении на n,
стремиться к нулю. Таким образом, формула
(40) вытекает из формулы Гаусса (см29) и
является общей при оценки точности
любых функций. Для функции вида U=kx
(41), где x-
измеренная величина, k-
постоянный
коэффициент, имеем
 , т.к.
, т.к.
 ;
dU=kdx
или
ΔU=kΔx.
СКО произведения постоянного коэффициента
на аргумент равна произведению постоянного
на СКО аргумента.
;
dU=kdx
или
ΔU=kΔx.
СКО произведения постоянного коэффициента
на аргумент равна произведению постоянного
на СКО аргумента.
 Средняя квадратическая
относительная ошибка измерения расстояний
нитяным дальномером равна 1/700. В.Функция
имеет линейный вид
Средняя квадратическая
относительная ошибка измерения расстояний
нитяным дальномером равна 1/700. В.Функция
имеет линейный вид
 (42), где
(42), где
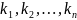 -
постоянные коэффициенты; x,y,…,w-
независимые аргументы, измеренные со
средними квадратическими ошибками
-
постоянные коэффициенты; x,y,…,w-
независимые аргументы, измеренные со
средними квадратическими ошибками
 .
По аналогии с функцией (41) на основе
формул (39),(40) имеем
.
По аналогии с функцией (41) на основе
формул (39),(40) имеем
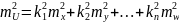 Квадрат СКО
линейной функции равен сумме произведений
квадратов постоянных на квадраты СКО
соответствующих аргументов.
Квадрат СКО
линейной функции равен сумме произведений
квадратов постоянных на квадраты СКО
соответствующих аргументов.
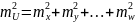 Квадрат СКО алгебраической суммы
аргументов равен сумме квадратов СКО
аргументов.
Квадрат СКО алгебраической суммы
аргументов равен сумме квадратов СКО
аргументов.
35. Средняя квадратическая ошибка среднего арифметического
Определим СКО
арифметической середины:
 перепишем это выражение в виде:
перепишем это выражение в виде:
 по формуле (42) при
по формуле (42) при
 ;
;
 имеем
имеем
 обозначив окончательно получим:
обозначив окончательно получим:
 СКО арифметической середины меньше
СКО одного измерения в
СКО арифметической середины меньше
СКО одного измерения в
 .
Это доказывает, что арифметическое
среднее из ряда измерений – наиболее
надежный результат. Ткаим образом,
увеличивая число измерений в разумных
пределах, можно повысить точность
окончательного результата (арифметического
среднего). Но если и дальше увеличивать
число n, то случайные
ошибки могут сравняться с состематическими
и даже будут меньше их и тогда последующее
увеличение числа измерений (приемов)
не даст желаемого повышения точности,
ибо систематические (постоянные) ошибки
не уменьшаются с увеличением n,
а остаются теми же и могут играть
определяющую роль в оценке результатов
измерений.
.
Это доказывает, что арифметическое
среднее из ряда измерений – наиболее
надежный результат. Ткаим образом,
увеличивая число измерений в разумных
пределах, можно повысить точность
окончательного результата (арифметического
среднего). Но если и дальше увеличивать
число n, то случайные
ошибки могут сравняться с состематическими
и даже будут меньше их и тогда последующее
увеличение числа измерений (приемов)
не даст желаемого повышения точности,
ибо систематические (постоянные) ошибки
не уменьшаются с увеличением n,
а остаются теми же и могут играть
определяющую роль в оценке результатов
измерений.
