27. Прямая геодезическая задача.

В геодезии часто приходится передавать координаты с одной точки на другую. Например, зная исходные координаты точки А (рис.23), горизонтальное расстояниеS_AB от неё до точки В и направление линии, соединяющей обе точки (дирекционный угол α_AB или румб r_AB), можно определить координаты точки В. В такой постановке передача координат называется прямой геодезической задачей.

Р ис. 23. Прямая геодезическая задача

Для точек, расположенных на сфероиде, решение данной задачи представляет значительные трудности. Для точек на плоскости она решается следующим образом. Дано: Точка А( X_A, Y_A ), S_AB иα_AB. Найти: точку В( X_B, Y_B ). Непосредственно из рисунка имеем: ΔX = X_B – X_A; ΔY = Y_B – Y_A.

Разности ΔX и ΔY координат точек последующей и предыдущей называются приращениями координат. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Их значения находим из прямоугольного прямоугольника АВС: ΔX = S_AB · cos α_AB ; ΔY = S_AB · sin α_AB . Так как в этих формулах S_AB всегда число положительное, то знаки приращений координат ΔX  и  ΔY зависят от знаков cos α_AB  и  sin α_AB. Для различных значений углов знаки ΔX и ΔY представлены в табл.1.

Знаки приращений координат ΔX и ΔY

Приращение координат	Четверть окружности в которую направлена линия
	I (СВ)	II (ЮВ)	III (ЮЗ)	IV (СЗ)
ΔX	+	-	-	+
ΔY	+	+	-­	-

При помощи румба приращения координат вычисляют по формулам: ΔX = S_AB · cos r_AB ; ΔY = S_AB · sin r_AB .

Знаки приращениям дают в зависимости от названия румба. Вычислив приращения координат, находим искомые координаты другой точки: Xb = xa + δx ; Y_B = Y_A+ ΔY  . Таким образом, можно найти координаты любого числа точек по правилу: координаты последующей точки равны координатам предыдущей точки плюс соответствующие приращения.

28. Обратная геодезическая задача.

Обратная геодезическая задача заключается в том, что при известных координатах точек А( X_A, Y_A ) и В( X_B, Y_B ) необходимо найти длину S_AB и направление линии АВ: румб r_AB  и  дирекционный угол α_AB (рис.24).

Р ис. 24. Обратная геодезическая задача

Данная задача решается следующим образом. Сначала находим приращения координат: ΔX = X_B – X_A ; ΔY = Y_B – Y_A.

ΔY	= tg rAB
ΔX

Величину угла r_AB определим из отношения

По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим α_AB.

SAB=	ΔX	=	ΔY	= ΔX · sec αAB = ΔY · cosec αAB
	cos αAB		sin αAB

Для контроля расстояние S_AB дважды вычисляют по формулам:

SAB=	ΔX	=	ΔY	= ΔX · sec rAB = ΔY · cosec rAB
	cos rAB		sin rAB

Р асстояние S_AB можно определить также по формуле

ЭЛЕМЕНТЫ ТЕОРИИ ОШИБОК ИЗМЕРЕНИЙ

29. Критерии точности измерений

Другая задача теории ошибок (оценка точности) решается благодаря установленным в теории вероятностей критериям. В качестве критериев оценки точности используется вероятная, средняя и средняя квадратическая ошибки. Вероятная ошибка r – это ошибка в середине ряда, все ошибки которого расположены по возрастанию или убыванию их абсолютных значений. Например, имеем ряд случайных ошибок: +4,-2,-1,-3,0,+2,+1,0. Расположим ошибки ряда по возрастанию абсолютных значений: 0,0,1,1,2,2,3,4. Вероятная ошибка равна 1,5 т.е. та ошибка, которая находиться в середине ряда. Средняя ошибка вычисляется по приближенной формуле: , где | | - абсолютная величина случайной ошибки. Наибольшее распространение в геодезии в качестве критерия оценок точности получила средняя квадратическая ошибка, предложенная К.Ф.Гауссом. Её значение вычисляется по формуле: , где [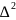 ]= для приведенного ряда имеем V=1,6 m=2,1 r=1,5.

Средняя квадратическая ошибка является более надёжным критерием оценки точности и обладает рядом достоинств: 1) крупные случайные ошибки, фактически определяющие качество измерений, окажут определяющее влияние на величину m, так как при вычислении средней квадратической ошибки случайные ошибки возводятся в квадрат. 2) даже при малом числе измерений получается достаточно надежная оценка точности. Так, если n=8 то для приведенного ряда ошибок средней квадратической ошибки =0,5 не будет превышать 25% от m, что практически считается малой величиной = 3) по величине m можно определить предельную ошибку: . В практике полевых работ допускается . При измерении линий можно применять относительную среднюю квадратическую ошибку, например

30 Средняя ошибка

С редней ошибкой   называют оценку среднего отклонения n₁ (центрального абсолютного момента первого порядка) и вычисляют по формуле:

31. Средняя квадратическая ошибка

Точность результатов измерений оценивается средней квадратической ошибкой. Средняя квадратическая ошибка одного измерения вычисляется по формуле: где [v²] – сумма квадратов вероятнейших ошибок; n – число измерений. Средняя квадратическая ошибка арифметической середины вычисляется по формуле:

32. Вероятная ошибка

Вероятная ошибка r – это ошибка в середине ряда, все ошибки которого расположены по возрастанию или убыванию их абсолютных значений. Например, имеем ряд случайных ошибок: +4,-2,-1,-3,0,+2,+1,0. Расположим ошибки ряда по возрастанию абсолютных значений: 0,0,1,1,2,2,3,4. Вероятная ошибка равна 1,5 т.е. та ошибка, которая находиться в середине ряда.

33. Предельная ошибка

Предельная ошибка не должна превышать утроенной средней квадратической ошибки, т.е. ε = 3 x m.

Иногда о точности измерений судят не по абсолютной величине средней квадратической или предельной погрешности, а по величине относительной ошибки.