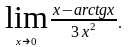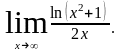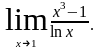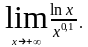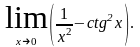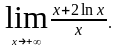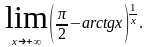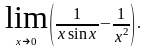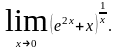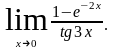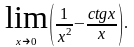- •2.12. Непрерывность функции
- •Задания для самостоятельной работы
- •3. Производные и дифференциалы
- •3.1. Понятие производной. Уравнение касательной и нормали к плоской кривой. Непрерывность дифференцируемой функции
- •Правила и формулы нахождения производных. Производная сложной функции
- •Производные основных элементарных функций (таблица производных):
- •Производные высших порядков
- •3.4. Понятие дифференциала и его геометрический смысл
- •Правило Лопиталя
- •Задания для самостоятельной работы
Правило Лопиталя
Теорема (Правило
Лопиталя). Пусть
функции
и
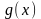 имеют в окрестности точки
непрерывные производные
и
имеют в окрестности точки
непрерывные производные
и
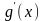 ,
и пусть
,
и пусть
 и
и
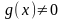 ,
,
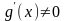 в окрестности точки
кроме, быть может, самой точки
.
Пусть существует
в окрестности точки
кроме, быть может, самой точки
.
Пусть существует
 .
Тогда
.
Тогда
 .
.
Если в окрестности
точки
функции
и
имеют вторые производные, причем
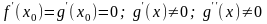 и существует
и существует
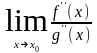 ,
то применяя правило Лопиталя к отношению
,
то применяя правило Лопиталя к отношению
 ,
получаем:
,
получаем:

Правило Лопиталя служит для раскрытия неопределенностей вида:
 или
или
 для вычисления пределов вида
для вычисления пределов вида

 для вычисления
пределов вида
для вычисления
пределов вида
 .
Произведение
.
Произведение
 следует преобразовать
в частное:
следует преобразовать
в частное:
 или
или
 ,
а далее применить
правило Лопиталя.
,
а далее применить
правило Лопиталя. для вычисления
пределов вида
для вычисления
пределов вида
 .
Разность
.
Разность
 следует преобразовать
в частное:
следует преобразовать
в частное:
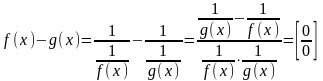 ,
,
а далее применить правило Лопиталя.
 для вычисления
пределов вида
для вычисления
пределов вида
 .
Если функции
и
попадают в перечисленные случаи, нужно
выполнить следующие действия:
.
Если функции
и
попадают в перечисленные случаи, нужно
выполнить следующие действия:
преобразовать выражение
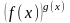 с помощью основного
логарифмического
тождества:
с помощью основного
логарифмического
тождества:
 ;
;вычислить предел произведения
 ,
которое во всех
перечисленных случаях имеет
неопределенность вида
;
,
которое во всех
перечисленных случаях имеет
неопределенность вида
;воспользоваться свойством непрерывности функции
 :
:
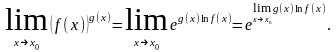
Пример. Вычислить пределы:
|
|
Решение:
 ;
;

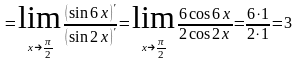 ;
;
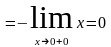 ;
;
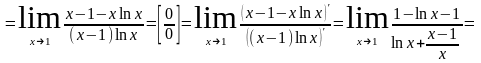
 ;
;

 .
.
Задания для самостоятельной работы
Найти производные данных функций:
|
|
Найти производную 2-го и 3-го порядка:
|
|
Найти дифференциалы функций:
|
|
Вычислить приближенно с помощью дифференциала:
|
|
|
|
Найти уравнение касательной и нормали к кривой
 в точке с абсциссой
в точке с абсциссой
 .
.Под каким углом наклонена к оси абсцисс касательная, проведенная к кривой
 в точке
в точке
 ?
?В какой точке кривой
 касательная параллельна прямой
касательная параллельна прямой
 ?
?В какой точке параболы
 нужно провести касательную, чтобы она
была перпендикулярна биссектрисе
первого координатного угла?
нужно провести касательную, чтобы она
была перпендикулярна биссектрисе
первого координатного угла?Найти точки пересечения с осями координат касательной, проведенной к графику функции
 в точке
в точке
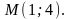
На кривой
 найти точку, касательная в которой
параллельна прямой
найти точку, касательная в которой
параллельна прямой

Точка движется прямолинейно, согласно заданному закону движения
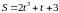 ,
где S –
путь (в м), t –
время (в с). Найдите скорость в момент
t =
2 с и ускорение в момент t =
3 с.
,
где S –
путь (в м), t –
время (в с). Найдите скорость в момент
t =
2 с и ускорение в момент t =
3 с.Точка движется прямолинейно, согласно заданному закону движения
 ,
где S –
путь (в м), t –
время (в с). Найдите тот момент времени,
когда ускорение равно 0.
,
где S –
путь (в м), t –
время (в с). Найдите тот момент времени,
когда ускорение равно 0.Зависимость пути от времени при прямолинейном движении точки задана уравнением
 (м).
В какой момент времени скорость
движения будет наибольшей? Какой путь
будет пройден к этому времени?
(м).
В какой момент времени скорость
движения будет наибольшей? Какой путь
будет пройден к этому времени?Зависимость пути от времени при прямолинейном движении точки задана уравнением
 .
Найдите максимальную скорость движения
этой точки.
.
Найдите максимальную скорость движения
этой точки.
Раскрыть неопределенности:
|
|
|

 ;
; ;
;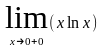
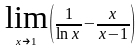 ;
; .
.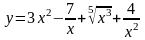 .
.

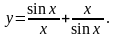
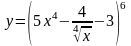 .
.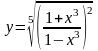 .
. .
.
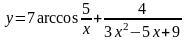 .
.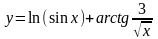 .
. .
.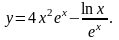
 .
. .
.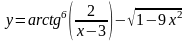 .
.



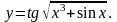








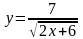 .
.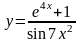 .
. .
.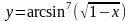 .
.
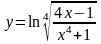 .
.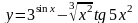 .
. .
. .
.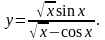
 .
. .
.
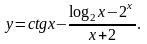




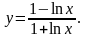
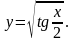

 .
.

 .
. .
.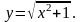

 .
. .
.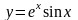 .
.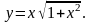
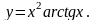


 .
. .
.


 .
.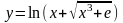 .
.


 .
.
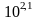 .
.
 .
.
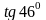 .
.