Правила и формулы нахождения производных. Производная сложной функции
Основные правила дифференцирования
Производная постоянной равна нулю, т. е.
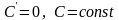.Производная аргумента равна единице, т. е.
.Производная алгебраической суммы конечного числа дифференцируемых функций равна алгебраической сумме производных этих функций, т. е.
.Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т. е.
.
Следствие 1.
Постоянный
множитель можно выносить за знак
производной:
.
Следствие 2.
Производная
произведения нескольких дифференцируемых
функций равна сумме произведений
производной каждого из сомножителей
на все остальные, например:
.
Производная частного двух дифференцируемых функций может быть найдена по формуле
(при
условии, что
).Производная сложной функции. Пусть задана сложная функция .
Теорема.
Если
и
дифференцируемые функции от своих
аргументов, то производная сложной
функции существует и равна производной
данной функции по промежуточному
аргументу и умноженной на производную
промежуточного аргумента по независимой
переменной
,
т. е.
.
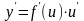Производные основных элементарных функций (таблица производных):
Производная логарифмической функции.
а)
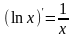и
,
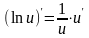где
функция зависящая от
.
б)
и
.
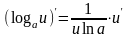Производная показательной функции.
а)
и
.
б)
и
.
Производная степенной функции.
и
.
Производная степенно-показательной функции.
.
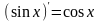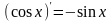Производная тригонометрических функций.
и
;
и
;
и
;
и
.
Производная обратных тригонометрических функц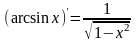ий.
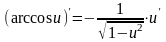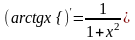и
;
и
;
и
;
и
.
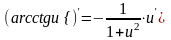Пример. Найти производные следующих функций:
а)
|
б)
|
в)
|
г)
|
;
;
;
.Решение:
а)
.
б)
.
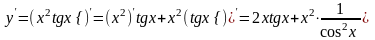в)
г)
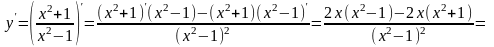
Производные высших порядков
Производной
2-го порядка
или второй
производной
функции
называется производная от ее первой
производной, т. е.
,
и обозначается
или
или
.
Аналогично
определяются и обозначаются: производная
3-го порядка
;
производная 4-го порядка
;
… производная
-го
порядка
.
Пример. Найти производную 2-го и 3-го порядка:
а)
|
б)
|
Решение:
а)
,
,
.
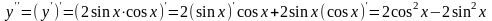б)
,
,
.
3.4. Понятие дифференциала и его геометрический смысл
Пусть функция
определена на промежутке
и дифференцируема в окрестности точки
,
тогда
или по теореме о связи бесконечно малых
с пределами функций имеем
,
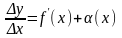где
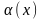
бесконечно малая величина при
.
Отсюда:
.
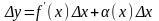Таким образом, приращение функции
состоит из двух слагаемых: 1.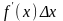 
линейного относительно
,
так как
;
2. 
нелинейного относительно
,
так как
.
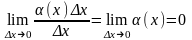Дифференциалом
функции
называется главная, линейная относительно
часть приращения функции, равная
произведению производной на приращение
независимой переменной:
.
Пример.
Найти приращение функции
при
и
.
Решение:
.
Ответ:
.
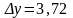Пример.
Найти дифференциал функции
.
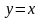Решение: По
формуле
имеем
.
Ответ:
Дифференциал
независимой переменной
равен приращению этой переменной:
.
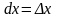Тогда формулу для
дифференциала функции можно записать
в виде:
.
Откуда
,
поэтому
можно рассматривать не только как
символическое обозначение производной,
но и как обычную дробь с числителем
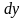и знаменателем
.
Геометрический
смысл. На
графике функции
(рис. 10) возьмем произвольную точку
.
Дадим аргументу
приращение
,
тогда функция получает приращение
.
В точке
проведем касательную, образующую угол
с осью
.
Из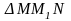 
видно,
что
.
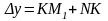Из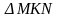 
имеем:
.
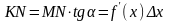Таким образом,
и соответствует формуле
.
Рис. 10
Следовательно, с геометрической точки зрения дифференциал функции есть приращение ординаты касательной, проведенной к графику функции в данной точке, когда получает приращение .
Свойства дифференциала аналогичны свойствам производной:
1)
|
4)
|
2)
3)
|
5)
|
.
.
.
.
.
Формула дифференциала
не изменится, если вместо функции от
независимой переменной
рассматривать функцию от зависимой
переменной
.
Это свойство дифференциала получило
название инвариантности
(т. е.
неизменности) формы дифференциала,
т. е.
.
Приближенные
вычисления с помощью дифференциала.
Согласно
формуле
,
т. е.
,
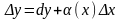при достаточно малых значениях
приращение функции
приблизительно равно ее дифференциалу
,
.
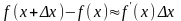Эту формулу часто используют в приближенных
вычислениях.
Пример.
Вычислить
.
Решение:
Пусть
.
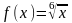Найдем
.
Положим
,
.
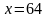Тогда, согласно формуле
,
для функции
имеем
.
Подставляем числовые значения:
.
Ответ:
.
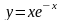