
- •2.12. Непрерывность функции
- •Задания для самостоятельной работы
- •3. Производные и дифференциалы
- •3.1. Понятие производной. Уравнение касательной и нормали к плоской кривой. Непрерывность дифференцируемой функции
- •Правила и формулы нахождения производных. Производная сложной функции
- •Производные основных элементарных функций (таблица производных):
- •Производные высших порядков
- •3.4. Понятие дифференциала и его геометрический смысл
- •Правило Лопиталя
- •Задания для самостоятельной работы
2.12. Непрерывность функции
Функция
 называется непрерывной
в точке
называется непрерывной
в точке
 ,
если она удовлетворяет следующим
условиям: 1) определена в точке
,
т. е. существует
,
если она удовлетворяет следующим
условиям: 1) определена в точке
,
т. е. существует
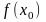 ;
2) имеет конечные односторонние пределы
функции при
;
2) имеет конечные односторонние пределы
функции при
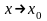 слева и справа; 3) эти пределы равны
значению функции в точке
,
т. е.
слева и справа; 3) эти пределы равны
значению функции в точке
,
т. е.
 .
.
Пример.
Исследовать
функции на непрерывность в точке
 :
а)
:
а) 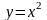 ,
б)
,
б)
 .
.
Решение:
а)
.
При
функция определена,
 ,
,
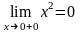 ,
,
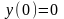 ,
т. е. все три условия непрерывности
функции в точке выполнены. Следовательно,
функция
в точке
непрерывна.
,
т. е. все три условия непрерывности
функции в точке выполнены. Следовательно,
функция
в точке
непрерывна.
б)
.
При
функция не определена;
 ;
;
 .
Таким образом в точке
функция не является непрерывной, так
как не выполнены первое и третье условия
непрерывности функции в точке.
.
Таким образом в точке
функция не является непрерывной, так
как не выполнены первое и третье условия
непрерывности функции в точке.
Функция
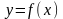 называется непрерывной
в точке
,
если она определена в этой точке и
бесконечно малому приращению аргумента
соответствует бесконечно малое приращение
функции:
называется непрерывной
в точке
,
если она определена в этой точке и
бесконечно малому приращению аргумента
соответствует бесконечно малое приращение
функции:
 .
.
Точка называется точкой разрыва функции , если эта функция в данной точке не является непрерывной. Различают точки разрыва:
устранимый
разрыв –
когда существуют конечные односторонние
пределы функции слева и справа при
,
равные друг другу:
 и они не равны значению
или
не существует. Например,
и они не равны значению
или
не существует. Например,
 .
Односторонние пределы равны:
.
Односторонние пределы равны: ,
однако функция не определена в точке
,
т. е.
–
точка устранимого разрыва. Этот разрыв
можно устранить, если доопределить
функцию:
,
однако функция не определена в точке
,
т. е.
–
точка устранимого разрыва. Этот разрыв
можно устранить, если доопределить
функцию:
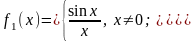 ;
;
первого рода
– когда существуют конечные односторонние
пределы функции слева и справа при
,
не равные друг другу:
 .
Например,
.
Например,
 .
Односторонние пределы равны:
.
Односторонние пределы равны: ,
т. е.
–
точка разрыва первого рода для функции:
,
т. е.
–
точка разрыва первого рода для функции:
 ;
;
второго рода
– когда хотя бы один из односторонних
пределов слева
 или справа
или справа
 равен бесконечности или не существует.
Например,
равен бесконечности или не существует.
Например,
 .
Односторонние пределы равны:
.
Односторонние пределы равны:
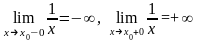 ,
т. е.
–
точка разрыва второго рода.
,
т. е.
–
точка разрыва второго рода.
Свойства функций, непрерывных в точке:
1. Если функции
и
 непрерывны в точке
,
то их сумма
непрерывны в точке
,
то их сумма
 ,
произведение
,
произведение
 и частное
и частное
 (при условии
(при условии
 )
являются функциями, непрерывными в
точке
.
)
являются функциями, непрерывными в
точке
.
2. Если функция
непрерывна в точке
и
 ,
то существует такая окрестность точки
,
в которой
,
то существует такая окрестность точки
,
в которой
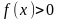 .
.
3. Если функция
 непрерывна в точке
непрерывна в точке
 ,
а функция
,
а функция
 непрерывна в точке
,
то сложная функция
непрерывна в точке
,
то сложная функция
 непрерывна в точке
.
Свойство можно записать:
непрерывна в точке
.
Свойство можно записать:
 ,
т. е. под знаком непрерывной функции
можно переходить к пределу.
,
т. е. под знаком непрерывной функции
можно переходить к пределу.
Функция
называется непрерывной
на промежутке
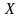 ,
если она непрерывна в каждой точке этого
промежутка. Все элементарные функции
непрерывны в области их определения.
,
если она непрерывна в каждой точке этого
промежутка. Все элементарные функции
непрерывны в области их определения.
Свойства функций, непрерывных на отрезке:
1. Если функция
непрерывна на отрезке
 ,
то она ограничена на этом отрезке.
,
то она ограничена на этом отрезке.
2. Если функция
непрерывна на отрезке
,
то она достигает на этом отрезке
наименьшего значения
 и наибольшего значения
и наибольшего значения
 (теорема Вейерштрасса).
(теорема Вейерштрасса).
3. Если функция
непрерывна на отрезке
и значения ее на концах отрезка
 и
и
 имеют противоположные знаки, то внутри
отрезка найдется точка
имеют противоположные знаки, то внутри
отрезка найдется точка
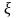 такая, что
такая, что
 .
(Теорема Больцано-Коши.)
.
(Теорема Больцано-Коши.)
Пример.
Исследовать
на непрерывность и найти точки разрыва
функции
 .
Установить характер разрыва.
.
Установить характер разрыва.
Решение:
При
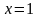 функция не определена, следовательно,
функция в точке
терпит разрыв:
функция не определена, следовательно,
функция в точке
терпит разрыв:
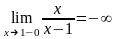 ,
а
,
а
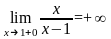 .
Так как односторонние пределы бесконечны,
то
точка разрыва второго рода.
.
Так как односторонние пределы бесконечны,
то
точка разрыва второго рода.
