10. Зависимость теплоёмкостей от давления и объёма.

Из общей формулы для теплоемкостей реальных и идеальных газов можно получить два соотношения:

,

.

Выводы из анализа этих соотношений:

-Изохорная теплоёмкость зависит от величины объёма системы(с_v=c_v(v)), если в уравнении состояния газа давление от температуры зависит нелинейно, т.е. const. Если давление газа в уравнении состояния зависит от температуры линейно, то c_vc_v(v).

-Изобарная теплоёмкость зависит от величины давления( c_p=c_p(p)), если удельный объём в уравнении состояния зависит от температуры нелинейно, т.е. при const . И наоборот,

при =const. , c_pc_p(p) .

В последнем случае не нужно опытным путем определять изобарную теплоемкость в лабораторных установках при различных значениях давления.

Для идеального газа .и тогда ,

следовательно, изохорная теплоёмкость идеального газа от величины объёма не зависит.

Для идеального газа . и тогда ,

следовательно, изобарная теплоемкость идеального газа от величины давления не зависит.

Исследуем зависимость изохорной теплоёмкости идеального газа от величины давления, то есть найдем , представив ее в виде произведения двух частных производных

. Но , а сжимаемость ,то , следовательно, изохорная теплоёмкость идеального газа от величины давления не зависит.

Исследуем зависимость изобарной теплоемкости идеального газа от величины объема:

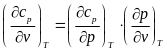, Но , а , то

следовательно, изобарная теплоемкость идеального газа от величины давления не зависит.

Общий вывод: изохорная и изобарная теплоёмкости идеального газа зависят только от температуры.

11. Зависимость теплоёмкости от температуры.

Истинная и средняя теплоёмкости.

Исследуем зависимость изохорной и изобарной теплоёмкости реальных и идеальных газов от величины температуры:

Поменять порядок дифференцирования и применить затем дифференциальные соотношения термодинамики не удается, то есть термодинамика на этот вопрос не отвечает.

Вывод: зависимость изохорной и изобарной теплоёмкости реальных и идеальных газов от температуры может быть установлена только опытным путём, либо с помощью какой-либо физической теории.

Опытные значения зависимости теплоёмкости от температуры представляются в виде таблиц, графиков и эмпирических зависимостей. У большинства технических газов c_v и c_p возрастают с ростом температуры.

Из физики известно, что температура газа не связана колебательным движением атомов и молекул, а зависит от кинетической энергии их поступательного движения. Подводимая к газу теплота по мере роста температуры перераспределяется всё более и более в пользу колебательного движения и поэтому прирост температуры при одинаковом подводе теплоты замедляется.

с

с₀

t

Рис.8. Зависимость теплоемкости от температуры.

На рис.8 опытные данные обозначены в виде звездочек. Сплошная линия – это кривая, аппроксимирующая опытные данные с использованием метода наименьших квадратов или других аналогичных математических методов. Аппроксимирующая кривая подчиняющаяся уравнению

c=c₀ + at + bt² + dt³ +…

Здесь: t-температура в градусах Цельсия ; c₀, a, b, d и т.д – эмпирические коэффициенты (коэффициенты, полученные опытным путем). В инженерных расчетах ограничиваются первыми двумя слагаемыми в правой части уравнения, то есть полагают зависимость теплоемкости от температуры линейной:

C = c₀ + at

В частности:

cv=c0v + at

и

cр=c0р + at

Все ранее полученные формулы относятся к истинной теплоемкости, то есть теплоемкости для конкретной (заданной) температуры

В практических расчётах часто требуется знать среднее значение теплоёмкостей в заданном интервале температур от t₁ до t_2.

_{Обознач}ение средней теплоемкости: , или _{. .}

Средняя теплоемкость определяется как средняя линия трапеции на рисунке:

рис.9.К

или окончательно

Рисунок. К определению средней теплоемкости

Конкретные значения эмпирических коэффициентов С₀ и а содержатся в справочной литературе по теплофизическим характеристикам веществ.

В тех случаях, когда зависимость теплоёмкости от температуры не удаётся удовлетворительно аппроксимировать линейной зависимостью вида c=c₀+at, то следует воспользоваться формулой для нелинейной зависимости:

Для оценочных (не очень точных) расчетов, когда отсутствуют опытные данные для теплоемкости в виде таблиц или эмпирических формул, можно воспользоваться результатами молекулярно-кинетической теории газов, в которой понятию идеального газа соответствуют одноатомные газы при малых давлениях

Из молекулярно-кинетической теории газов известно соотношение U_ = 12,56T, КДж/кмоль.

Здесь U_ - внутренняя энергия одного киломоля идеального газа, Т - абсолютная термодинамическая температура, К.

Для массовой изохорной теплоемкости идеального газа, ранее было получено: Молярная изохорная изобарную теплоемкость определяется аналогично:

Подставляя в c_v значение U_ = 12,56T получим

c_v =12,56, КДж/(кмоль*К)

Молярную изобарную теплоемкость с_µp найдем из уравнения Майера:

c_p=c_v+R_=12,56+8,314 20,93 КДж/(кмоль*К)

Как следует из полученных результатов, по молекулярно-кинетической теории газов теплоемкости не зависят от температуры, то есть берутся средним значениеми во всем диапазоне температур. Именно в этом заключается оценочный характер этих значений.

На практике, чаще всего приходится иметь дело с двухатомными, трехатомными и более атомными газами. Воздух считается в инженерных расчетах двухатомным газом, состоящим по объёму на 79% из азота (N₂) и на 21% из кислорода (O₂).

Для оценочных расчетов можно пользоваться следующей таблицей теплоемкостей идеальных газов:

Газ	cv,	cp,
Одноатомный	12,56	20,93
Двухатомный	20,93	29,31
Трех и более атомный	29,31	37,68

В этой таблице, во второй и третьей строках теплоемкости скорректированы по результатам опытов.

У реальных газов, в отличие от идеального, теплоёмкости могут зависеть не только от температуры, но и от объёма и давления.