
Изгиб
.pdf
навантаження в перерізах балки виникає сумарний згинальний момент
(MxF + Mx ) . Робота двох сил визначиться як:
W = W + W + W |
= |
1 |
F |
11 |
+ |
|
1 |
1 δ |
22 |
+1 |
21 |
, |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
3 |
1 |
|
2 |
|
|
|
2 |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а потенційна енергія |
пружної |
|
деформації |
виразиться через сумарний |
|||||||||||||||||||||||||||||
згинальний момент як: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(M |
|
+ |
|
|
|
)2 dz |
|
|
|
|
M 2 dz |
|
|
|
|
|
2 dz |
|
M |
|
|
|
|
|
||||||||
|
xF |
M |
x |
|
|
|
|
|
|
|
M |
|
xF |
M |
x |
|
|||||||||||||||||
U3 = ∫ |
|
|
|
|
|
|
|
|
= ∫ |
|
|
xF |
|
|
+ ∫ |
|
|
x |
|
+ ∫ |
|
|
dz . |
||||||||||
|
|
2EIx |
|
|
|
|
|
|
2EIx |
|
|
|
2EIx |
|
EIx |
|
|||||||||||||||||
l |
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
l |
|
l |
|
|
|
|||||||||||
Порівнюючи вирази дляW3 , U3 , після нескладних перетворень одержимо: |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
M xF |
|
x |
dz . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
21 = ∫ |
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.5) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
l |
|
|
EIx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Порядок визначення переміщень за допомогою інтеграла МаксвеллаМора.
1.Прикладаємо зовнішнє навантаження, визначаємо опорні реакції, розбиваємо балку на ділянки, записуємо вирази (функції) згинаючого моменту MxF для кожної ділянки.
2.У точці, переміщення якої визначаємо, прикладаємо:
a)Одиничну силу при визначенні прогину (лінійного переміщення);
b)Одиничний момент при визначенні кутового переміщення.
Визначаємо опорні реакції й у такому ж порядку, як і для зовнішнього навантаження, на кожній ділянці записуємо вирази (функції) згинаючого
моменту Mx .
3.Підставляємо функції (вирази) MxF і Mx в інтеграл Максвелла-Мора та робимо відповідні обчислення.
41
4. Результат обчислень позитивний, якщо напрямок одиничного
навантаження, що прикладається, збігається з напрямком дійсного переміщення, і негативний, якщо напрямок одиничного навантаження, що прикладається, не збігається з напрямком дійсного переміщення.
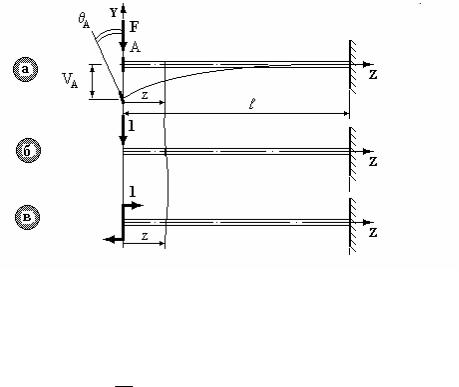
Приклад 2. Консольна балка постійного поперечного перерізу (ЕIx=const) довжиною l навантажена на кінці зосередженою силою F(рис.3.4а). Визначити прогин VA та кут θA повороту на кінці консолі.
Рис. 3.4.
1.Запишемо функцію MxF = −Fz (рис.3.4а).
2. У точці A прикладаємо одиничну силу (рис.3.4б) та записуємо функцію Mx = −1 z .
3. |
|
|
|
Підставляючи MxF й |
M |
x в інтеграл, одержимо: |
||
|
|
1 l |
|
Fl3 |
||||
V |
= |
|
|
F z z dz = |
|
(див. приклад 1 на рис. 3.2). |
||
EIx 0∫ |
|
|||||||
A |
|
|
3EIx |
|||||
42
4.Для визначення кутового переміщення у точці A
прикладаємо одиничний момент (рис.3.4в) та записуємо функцію
|
|
x =1. |
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
5. |
|
|
Підставляючи |
MxF |
й |
|
x |
в |
інтеграл, |
|||
|
|
M |
||||||||||
одержимо: θA = |
1 l |
|
|
Fl2 |
|
|
|
|
|
|||
|
∫(−F z) 1 |
dz = − |
|
. |
|
|
|
|
||||
|
2EIx |
|
|
|
|
|||||||
|
|
|
EIx 0 |
|
|
|
|
|
|
|
||
Результат обчислення прогину VA позитивний, тому що прикладена
одинична сила збігається з напрямком дійсного переміщення. Результат обчислення кута повороту θA негативний, тому що
прикладений одиничний момент по напрямку не збігається з дійсним напрямком кута повороту перерізу в точці A .
3.2.2Геометричний спосіб обчислення інтеграла Максвела-Мора. Спосіб перемножування епюр.
Рис. 3.5.
43

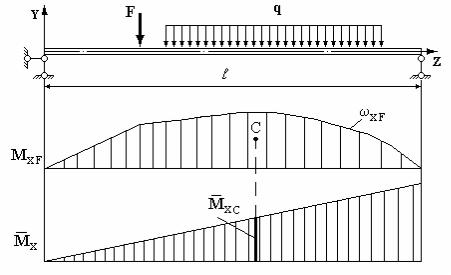
Правило Верещагіна. Використовуючи геометричну інтерпретацію визначення інтегралу як значення площі, інтеграл Мора для визначення переміщень у балках постійного перерізу можна обчислити за допомогою спеціальної операції над епюрами відповідних згинальних моментів.
В результаті одержимо:
|
MxF |
|
|
|
ωxF |
|
xC |
|
|
ij = ∫ |
M |
x |
dz = |
M |
, |
(3.6) |
|||
|
|
|
|
|
|
||||
l |
EIx |
EIx |
|
||||||
де ωxF - площа вантажної (від зовнішнього навантаження) епюри MxF ;
MxC - ордината, узята з одиничної епюри Mx під центром ваги C
вантажної епюри.
Правило знаків. Якщо епюри, що перемножуються, лежать по одну сторону (обидві нагорі або внизу), добуток позитивний; якщо епюри, що перемножуються, лежать по різні сторони - добуток негативний.
Якщо епюра від зовнішнього навантаження кусочно-лінійна на ділянках, а одинична епюра завжди кусочно-лінійна, результат перемножування не залежить від порядку використання співмножників, тобто:
ωxF |
|
|
|
|
x MFC |
, |
|
|
xC |
= |
ω |
|
|||
М |
(3.7) |
||||||
|
|
|
|
|
|||
EIx |
|
EIx |
|
||||
деωxF - площа епюри від зовнішнього навантаження; ωx - площа епюри від одиничного навантаження; MFC - ордината під центром ваги одиничної Mx
епюри, узята з епюри MxF від зовнішнього навантаження.
44

Якщо епюри MxF і Mx складаються з декількох ділянок, то перемножування здійснюється по ділянках, а результат підсумовується, тобто:
n |
ω |
|
|
|
|
|
|
ixF |
M |
ixC |
|
|
|||
ij = ∑ |
|
|
|
. |
(3.8) |
||
|
EIx |
|
|||||
i=1 |
|
|
|
|
|||
Відзначимо, що в розглянутих задачах епюри вантажних та одиничних згинальних моментів складаються з досить простих площ: прямокутник, трикутник, параболічний трикутник і т.д. У таблиці приведені площі ω та координати центрів ваги zc плоских фігур, що зустрічаються в епюрах.
При рішенні конкретних задач доцільно використовувати правило трапеції для перемножування лінійних епюр і правило СимпсонаКарнаухова для перемножування будь-яких епюр (у більшості випадків нелінійних).
45
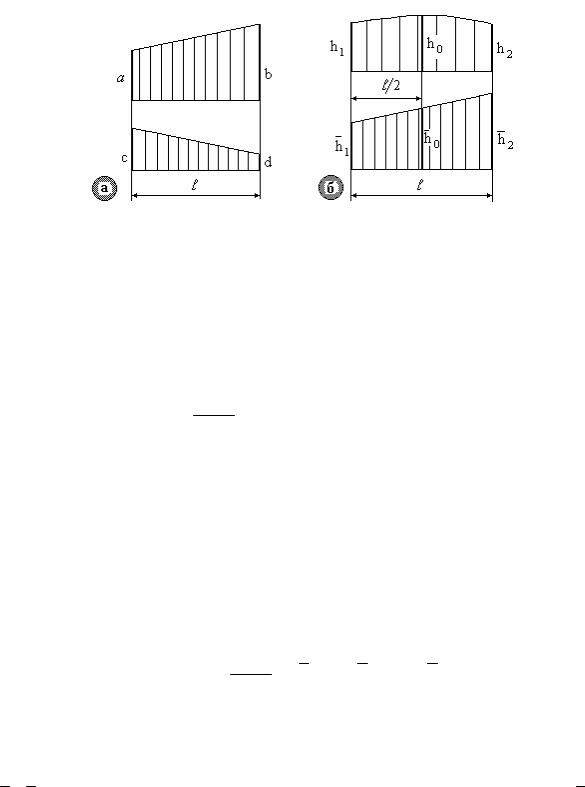
Рис.3.6.
Правило трапеції (тільки для лінійних епюр – рис.3.6а). У тому випадку,
коли на ділянці епюра MxF від зовнішнього навантаження лінійна,
перемножування епюр можна виконати за правилом трапеції. Результат перемножування лінійних епюр на ділянці довжиною lдорівнює:
= 6EIl x (a d + b c + 2 a c + 2 b d) .
Правило знаків: якщо ординати, що перемножуються, одного знака
(лежать по одну сторону), одержуваний добуток позитивний, якщо знаки ординат різні - добуток негативний.
Правило Симпсона - Карнаухова (для лінійних епюр і епюр, описуваних квадратною параболою-рис.3.6б). Результат добутку наступний:
= 6EIl x (h1h1 + h 2 h 2 + 4h 0 h 0 ) .
Тут h1 , h 2 - крайні ординати вантажної епюри (нелінійної) на ділянці; h1 , h 2 - крайні ординати одиничної епюри (лінійної) на ділянці; h0 і h0 -
середні ординати епюр на ділянці. Правило знаків при перемножуванні ординат аналогічно правилу трапеції.
46
Приклад 3. Для консольної балки, навантаженої зовнішніми силами, як показано на рис.3.7, визначити прогин та кут повороту на кінці консолі в перерізі A .
1.Визначаємо опорні реакції.
∑Fyi = 0 ; F −q 3a +R B = 0 R B = 2qa .
∑M Bi = 0 ; −F 6a +q 3a 3,5a −MB = 0 MB =1,5qa2 .
Перевірка:
∑MAi = −q 3a 2,5a −M + RB 6a −MB = qa2 (−7,5 −3 +12 −1,5) ≡ 0. 2.Записуємо вирази Qy і Mx , будуємо відповідні епюри.
0 ≤ z1 ≤ a : Q y = F = qa ; M x = F z1 = qa z1.
0 ≤ z 2 |
≤ 3a |
: Q y = F −q z 2 = qa −q z 2 . Поперечна сила змінює знак при |
|||||
z = a . |
|
|
|
|
|
|
|
|
|
|
z 2 |
|
z 2 |
||
M x = F(z 2 |
+a) −q |
2 |
= qa(z +a) −q |
2 |
. |
||
2 |
2 |
||||||
|
|
|
|
|
|||
47

|
|
|
|
|
|
|
|
|
|
|
Рис.3.7. |
||
M |
x мах |
= M |
x |
|
z=a |
= 2qa 2 −0,5qa 2 =1,5qa 2 ; |
|||||||
|
|||||||||||||
|
|
|
|
|
1,52 |
|
|
|
|||||
M |
x |
|
z=1,5a |
= qa 2 (2,5 − |
) =1,375qa 2 . |
||||||||
|
|||||||||||||
|
|
||||||||||||
|
|
|
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
0 ≤ z3 ≤ 2a : Q y = −2qa ; M x = −M B +R B z = −1,5qa 2 +2qa z . |
|||||||||||||
3.У |
|
точці |
A |
прикладаємо одиничну силу, будуємо епюру |
|
x = −1 z , |
|||||||
|
M |
||||||||||||
визначаючи ординати на границях кожної ділянки. 4.Перемножуючи епюри Mx і Mx , визначаємо шуканий прогин:
48

V = |
qa4 |
[− |
1 |
1 |
1 |
2 |
1 |
+ |
3 |
(−1 |
1+ 4 |
0,5 −4 1,375 2,5) + |
2 |
(−2,5 |
6 |
+ |
||||
|
|
|
|
|
|
|
||||||||||||||
A |
EIx |
|
2 |
|
|
3 |
|
|
6 |
|
|
|
|
6 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
+ 4 1,5 −2 2,5 4 + |
2 1,5 6)] = |
qa4 |
|
[−2 −38,25 −22] = − |
10,375qa4 |
|
. |
|||||||||||||
6EIx |
|
|
EIx |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тут на першій ділянці перемножування епюр виконано за правилом Верещагіна; на другій - Симпсона, на третій - трапеції. Знак мінус указує на те, що під дією зовнішнього навантаження переріз переміщується угору.
5.У точці A прикладаємо одиничний момент, будуємо епюру Mx =1.
Перемножуючи її по ділянках з вантажною епюрою, визначаємо кут повороту перерізу A.
θA |
= |
qa3 |
[ |
1 |
1 |
1 1 |
+ |
|
3 |
(1 |
1−0,5 1 |
+ 4 1,375 |
1) + |
|
|
|||
EIx |
2 |
6 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
qa3 |
|
4,5qa3 |
|
+ |
|
(2,5 1−1,5 1+ 2 |
2,5 |
1−2 1,5 |
1)] |
= |
|
[0,5 +3 +1] = |
|
. |
||||||||
6 |
EIx |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EIx |
|||
Тут на першій ділянці перемножування виконане за правилом Верещагіна, на другій - Симпсона, на третій - трапеції. Результат обчислень позитивний, отже, напрямок кута повороту перерізу A збігається з напрямком одиничного моменту.
49
3 4. ЗАГАЛЬНІ ВКАЗІВКИ ПО ВИКОНАННЮ РОЗРАХУНКОВОПРОЕКТУВАЛЬНИХ РОБІТ
І ВИМОГИ ДО ЇХНЬОГО ОФОРМЛЕННЯ
Опір матеріалів займає найважливіше місце серед фундаментальних дисциплін у циклі загальноінженерної підготовки студентів.
Задача курсу – придбання майбутніми інженерами практичних навичок розрахунків на міцність.
Приступаючи до виконання роботи, студент повинний:
вивчити за конспектом і додатковою навчальною літературою теоретичний матеріал відповідного розділу курсу;
проробити приклади і задачі, які були розв’язані на лекціях і практичних заняттях;
проаналізувати вихідні дані і постановку задачі і намітити план її виконання;
зробити вихідні викладення: намалювати схему балки, записати необхідні для рішення задачі формули і рівняння (рівняння статичної рівноваги і т.д.).
оформити задачу в чернетці і, у разі потреби, проконсультуватися у викладача.
Розрахунки необхідно робити в загальному виді з проміжними викладеннями в звичайних чи десяткових дробах, зберігаючи усюди три значущі цифри.
Для побудови епюр внутрішніх силових факторів, напружень і переміщень необхідно правильно вибрати масштаб по координатних осях, проставити позначення відповідного параметра і його розмірність, а потім по необхідному числу крапок побудувати графік.
50
