
Изгиб
.pdf
|
1 |
= |
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ey |
|
σ |
|
M |
|
|
||||
ρ |
|
|
|
|
= |
x |
. |
||||
|
1 |
|
|
|
|
|
|
||||
= |
|
|
Ey |
|
|
||||||
|
M x |
|
|
EIx |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
EIx |
|
|
|
|
|
|
|||
Формула для визначення нормальних напружень прийме вигляд:
σ = M x y . (2.7) Ix
З отриманої формули випливає, що нормальні напруження σ по висоті перерізу змінюються лінійно, тому що згинальний момент M x та момент інерції Ix перерізу величини постійні. На рис 2.4 показані розподіли нормальних напружень по висоті для різних за формою перерізів.
Максимальні напруження σmax виникають у найбільш віддалених точках від нейтральної лінії при y = ymax , тобто
Рис.2.4.
21

σmax = |
M x ymax |
, |
що повинні |
зіставлятися |
з допустимим |
||
|
|||||||
|
I x |
|
|
|
|
|
|
напруженням [σ]. |
|
|
|
|
|
||
Таким чином умова міцності при згинанні прийме вигляд: |
|||||||
|
σmax = |
|
M x max ymax |
|
≤ [σ]. |
(2.8) |
|
|
|
Ix |
|||||
|
|
|
|
|
|
||
На практиці цей вигляд використовується для розрахунку перерізів, що
мають одну вісь симетрії (рис. 2.4б). З обліком того, що Wx = |
Ix |
- |
|
||
|
ymax |
|
осьовий момент опору, то для перерізів із двома осями симетрії (рис. 2.4а) зручніше використовувати умову міцності при згинанні у вигляді:
σmax = |
M x max |
≤ [σ]. |
(2.9) |
|
|||
|
Wx |
|
|
У випадку поперечного згинання, коли поперечна сила Qy не дорівнює нулю, відбувається скривлення поперечних перерізів, і гіпотеза плоских перерізів не дотримується. Як показують дослідження, при відношенні довжини l стержня до висоти h поперечного перерізу hl ≥8 (для більшості
балок) можна вважати, що поперечний переріз практично не скривляється, тоді формула (2.7) для визначення нормальних напружень справедлива і при поперечному згинанні.
22

Приклад. Визначити розміри різних форм поперечних перерізів, якщо згинальний момент в перерізі Mx = 80 кНм, допустиме напруження при згинанні [σ]=160 МПа.
З умови міцності σmax = |
M x max |
≤ [σ] |
осьовий момент опору |
перерізу |
|||||||||
Wx |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
M |
x max |
|
80 103 |
|
−3 |
|
3 |
|
3 |
|
||
Wx ≥ |
|
= |
|
= 0,5 10 |
|
м |
|
= |
500 см . Далі проектуємо |
переріз |
|||
[σ] |
160 106 |
|
|
||||||||||
(рис.2.5).
1. Прямокутний переріз (рис.2.5а), для якого повинне задаватися
відношення |
|
h |
b |
(візьмемо |
h |
b |
= 2 ). |
|
|
|
Осьовий |
|
момент |
опору |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
bh |
2 |
|
2 |
|
3 |
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|||
Wx = |
|
|
= |
|
b |
|
|
= 500 см , |
відкіля b |
= |
|
|
|
750 ≈ 9 см. Висота |
перерізу |
||||||||
6 |
|
3 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
h =18 см, площа поперечного перерізу A = bh = 2b2 =162 см2. |
|
||||||||||||||||||||||
2. Прямокутний переріз з відношенням |
h |
|
= |
|
1 |
(рис.2.5б). За аналогією: |
|||||||||||||||||
b |
|
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
осьовий |
|
|
момент |
опоруWx = |
bh 2 |
|
= |
|
b3 |
= 500 см |
3 |
, |
відкіля |
||||||||||
|
|
6 |
|
24 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
b = 3 12000 = 22,8 см, h =11,4см, A = 22,8 11,4 = 260 см2.
23

|
|
|
Рис.2.5. |
|
|
|
|
|||
3. |
Круглий суцільній переріз діаметром d (рис.2.5в). Осьовий момент |
|||||||||
|
опору |
Wx = πd3 |
≈ 0,1d3 = 500 |
см3, |
відкіля діаметр перерізу: |
|||||
|
|
32 |
|
|
|
|
|
|
|
|
|
d = 3 5000 =17,1см, площа A = |
πd 2 |
= |
π 17,12 |
= 229 см2. |
|||||
|
|
|
||||||||
|
|
|
4 |
|
|
4 |
|
|
|
|
4. |
Кільцевий переріз (рис.2.5г). Задаються відношенням діаметрів α = |
d |
, |
|||||||
|
||||||||||
|
|
|
|
|
|
|
|
|
D |
|
|
осьовий |
момент |
опору: Wx = |
πD3 |
(1 − α4 ) ≈ 0,1D3 (1 − α4 ) = 500см3. |
|||||
|
|
|
|
|
32 |
|
|
|
|
|
Нехай α = 0,8 , тоді |
|
5000 |
|
см, |
d = 20,4 0,8 =16,32 см. |
||||
D = 3 |
1 − 0,84 = 20,4 |
||||||||
Площа перерізу A = |
πD2 |
|
2 |
|
π 20,42 |
|
2 |
2 |
|
|
4 (1−α |
|
|
|
|||||
|
|
) = |
4 |
(1−0,8 |
|
) =115см . |
|||
5.Двотавровий переріз (рис.2.5д). За ДСТ 8239-72 підбираємо номер двотавра з найближчим більшим значенням осьового моменту опору до розрахункового. Так, для двотавра №30а: Wx = 518см3, A ≈ 50 см2.
24

6.Швелерний переріз (рис.2.5е). За ДСТ 8240-72 підбираємо номер швелера з найближчим більшим значенням осьового моменту опору до
розрахункового. Так, для швелера №33 Wx = 484 см3, A ≈ 47 см2.
Узявши відношення окремих площ до площі раціонального поперечного перерізу (двотавр, швелер), одержимо коефіцієнт перевитрати матеріалу. Складемо таблицю (рис.2.5), з якої випливає, що
самими раціональними є двотавровий і швелерний перерізи, y яких найменша площа поперечного перерізу та найменша витрата матеріалу.
2.2 Дотичні напруження при поперечному згинанні.
Дія в перерізі поперечної сили Qy викликає дотичні напруження τ, що
збігаються по напрямку з нею, по ширині перерізу не змінюються та визначаються за формулою Д.И.Журавського:
τ = |
Q ySвідсx |
|
b y Ix , |
(2.10) |
де Qy - поперечна сила, що діє в перерізі; Ix - осьовий момент інерції
перерізу щодо центральної осі X (нейтральної лінії); b y - ширина перерізу
на тім рівні у від нейтральної лінії, де визначаються дотичні напруження; Sвідсx = Aвідс yc - абсолютне значення статичного моменту щодо
центральної осі X частини перерізу, що лежить вище чи нижче того рівня, де визначаються дотичні напруження. Умова міцності по дотичним напруженням при поперечному згинанні записується у вигляді:
25
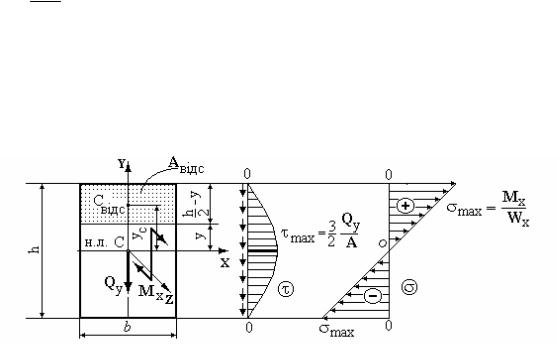
τmax |
= |
Q y maxSвідсx |
max |
≤[τ] |
(2.11) |
b y I x |
|
||||
|
|
|
|
|
Таким чином, при прямому поперечному згинанні маємо умови міцності по нормальним σ та дотичним τ напруженням. Основним вважається умова міцності по нормальним напруженням, а умова (2.11) по дотичним напруженням, як правило, перевіряється. Використання формули Д.И.Журавського розберемо на прикладах.
2.3 Розподіл дотичних напружень для прямокутного перерізу.
В перерізі діють Мх момент і поперечна силаQy , спрямовані, як показано на рис.2.6. Поперечна сила Qy , ширина перерізу b y = b та осьовий момент
інерції Ix = bh3 конкретні постійні величини (рис.2.6). Таким чином, 12
дотичні напруження змінюються за таким же законом, що і статичний
|
Sвідс |
|
момент відсіченої частини площі |
x |
. |
Рис.2.6.
26

Визначаємо дотичні напруження на рівні y. Площа відсіченої частини
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
bh |
|
|
|
2y |
|
|
|
|
|
|
|
|
|
|
||||||||
перерізу |
Aвідс = b |
|
|
|
− y |
= |
|
|
1 |
− |
|
|
|
|
|
|
, |
положення |
її |
центра ваги |
|||||||||||||||||||
|
|
|
|
2 |
|
|
h |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
h |
|
|
h |
− y |
h |
|
|
y |
|
|
|
|
h |
|
|
|
|
2y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
yc = |
|
− |
|
|
= |
|
+ |
|
|
|
|
= |
|
|
|
1 |
+ |
|
|
. |
|
|
|
Статичний |
момент |
|
відсіченої |
||||||||||||
2 |
|
2 |
|
|
2 |
4 |
h |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
частини площі: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Sвідсх = Aвідс |
|
|
|
|
|
|
bh |
|
|
2y |
|
|
|
|
|
h |
|
|
2y |
bh 2 |
|
2y |
|
2 |
|||||||||||||
|
|
yc |
= |
|
|
|
|
1 |
− |
|
|
|
|
|
|
|
1 |
+ |
|
= |
|
1 |
− |
|
|
. |
|||||||||||||
|
|
|
2 |
|
h |
|
4 |
|
|
8 |
h |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким |
чином, |
дотичні |
|
напруження |
|
|
змінюються |
за |
законом |
|
квадратної |
||||||||||||||||||||||||||||
параболи. Максимальні дотичні напруження виникають на нейтральній лінії, де нормальні напруження σ дорівнюють нулю. Для визначення τmax необхідно обчислити статичний момент половини площі перерізу Sвідсx max , і максимальні дотичні напруження визначаться
|
|
|
|
|
Q |
у |
Sвідс |
max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
як: τmax = |
|
|
x |
. |
|
Для |
прямокутного |
|
|
|
перерізу |
b = b y , |
|||||||||||
|
|
b y Ix |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
bh 3 |
|
|
|
відс |
|
|
bh 2 |
|
|
Q y bh 2 |
8 |
|
3 Q y |
|
3 Q y |
|
|||||
Ix |
= |
|
|
, |
Sx |
max |
= |
|
маємо: τmax = |
|
|
= |
|
|
|
= |
|
|
|
. |
|||
12 |
|
8 |
b bh3 12 |
2 bh |
2 A |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2.4 Розподіл дотичних напружень для двотаврового перерізу.
. В перерізі діють згинальний Мх момент та поперечна силаQy ,
спрямовані, як показано на рис.2.7.
27

Рис.2.7.
Використовуючи вираз (2.10) для дотичних напружень, визначимо їхні значення в характерних точках.
Точка 1: τ1 = 0, тому що Sвідсx = 0 (вище рівня 1 відсічена площа відсутня).
Точки 2,3. Ці точки мають однакову координату y, але належать полиці та стінці одночасно , тобто різній ширині b2=b; b3=d. Тому в місці переходу
полки в стінку виникає скачок дотичних напружень.
Точка 2 (приналежна полиці): τ2 = |
Qy |
|
|
|
|
|
h − t |
|
|
|
Q y t |
h − t |
||||||||||||||||||
|
|
|
|
bt |
|
|
|
|
= |
|
|
|
|
|
|
; |
||||||||||||||
b Ix |
|
|
|
Ix |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|||||||||||
Точка 3 (приналежна стінці): τ3 = |
|
Qy |
|
|
|
|
|
h − t |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
bt |
|
|
|
; |
|
|
|
|
|
|
|
|
|
||||||||||||||
d Ix |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Q y |
|
h − t |
h |
|
|
|
|
|
|
|
− t |
|
|
Q ySвідсx max |
|
|
|||||||||||||
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||
Точка 4: τ4 = |
|
bt |
|
|
+ d |
|
|
− t |
|
|
|
|
|
= |
|
|
|
|
|
|
|
. |
|
|||||||
|
|
|
|
|
|
|
|
dIx |
|
|
|
|
||||||||||||||||||
|
bIx |
|
2 |
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Sвідсx max - статичний момент щодо центральної осі половини площі перерізу, для стандартних профілів приведений у таблицях сортаменту.
28

Зразковий графік розподілу дотичних напружень приведений на рис 2.7. Дійсний розподіл дотичних напружень трохи відрізняється від отриманого, тому що полиці мають ухили, а перехід від полиці до стінки здійснюється по радіусу кривини.
2.5 Порядок виконання проектувального розрахунку при згинанні.
1.З умови міцності по нормальним напруженням визначаємо осьовий момент опору поперечного перерізу, тобто Wx ≥ M[xσmax] , та проектуємо
переріз.
2.Перевіряємо переріз по дотичним напруженням. Якщо τmax ≤[τ] , то розрахунок закінчений. Якщо τmax >[τ] (перевищення більш 5%), то розміри перерізу визначаються з умови міцності по дотичним напруженням. По нормальним напруженням перевіряти немає необхідності, тому що його розміри будуть більше первісного.
Приклад 1. Для даної схеми навантаження балки (рис.2.8) визначити розміри двотаврового поперечного перерізу, якщо допустиме нормальне напруження [σ] =150 Мпа, дотичне -[τ] =100 Мпа.
Визначаємо реакції:
∑M A = Fa + F(l + a) − RB l = 0, RB = 45кН;
∑M B = F(l+a) + Fa − RAl = 0, RA = 45кН.
Перевірка: ∑Fy = −F + F + RA − RB ≡ 0 .
1.Розбиваємо балку на три ділянки, записуємо для поточного перерізу на кожній ділянці вирази (функції) Qy і Mx :
29

0 ≤ z1 ≤ a Q y = −F = 30 кН; Mx = −F z1;
0 ≤ z2 ≤ l Q y = −F + R A = +15кН; M x = −F(z2 + a) + R A z2 ; 0 ≤ z3 ≤ a Q y = −F = −30 кН; Mx = −F z3 .
Обчислюємо Qy і Mx в характерних перерізах та будуємо епюри.
Рис.2.8.
2. З умови міцності по нормальним напруженням (де Mx max ) - небезпечний переріз на опорах; з умови міцності по дотичним напруженням (де Qy max )
рівнонебезпечним є будь-який переріз на консолях. Таким чином, Mx max =24 кНм; Qy max =30 кН.
3. З умови міцності по нормальним напруженням визначаємо момент опору:
|
M |
x max |
|
|
24 10 |
3 |
|
−3 |
3 |
3 |
Wx ≥ |
|
|
= |
|
|
|
= 0,16 10 |
|
м = 160 |
см . |
[σ] |
150 106 |
|
||||||||
|
|
|
|
|
|
|||||
По таблицях ДСТ вибираємо двотавр №18а Wx =159см3 , що незначно менше розрахункового значення.
30
