
IDZ_Opredelennyj_integral
.pdf
9.11.y =(x +1)2 , y2 = x +1.
|
|
|
|
19.13. |
y = x 36 − x2 , y = 0, |
||
(0 ≤ x ≤ 6). |
|||
9.15. |
y = arctg x, |
y = 0, |
|||||||||
x = |
|
|
|
|
|
|
|
|
|
||
3. |
|
|
|
|
|||||||
|
x = |
|
|
|
|
|
|
x = 0, |
|||
9.17. |
|
|
|
ey −1, |
|||||||
y = ln 2. |
|
|
|
|
|||||||
|
|
|
|
|
|||||||
|
y = |
|
|
|
|
x |
|
|
, |
y = 0, |
|
9.19. |
|
|
|
|
|
|
|
||||
1+ |
x |
||||||||||
|
|
|
|||||||||
x=1.
9.21.x =(y −2)3 ,
x= 4y −8.
|
y = |
|
|
|
x |
|
, |
|
|
y = 0, |
|
|
|
|
|
|
|
|
|
||||
|
( |
x |
2 |
) |
2 |
|
|
||||
9.23. |
|
|
|
+1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
x =1. |
|
|
|
|
|
|
|
|||
9.25. x = |
|
|
|
|
1 |
|
|
|
, |
x = 0, |
|
y |
|
|
|
|
|
||||||
1+ln y |
|||||||||||
|
y =1, |
|
y = e3 . |
|
|
|
|||||
y = x2 16 − x2 , y = 0,
9.27.(0 ≤ x ≤ 4).
9.29.y =(x −1)2 , y2 = x −1.
9.31.x = 4 −(y −1)2 , x = y2 −4y +3.
9.12.y = 2x − x2 +3, y = x2 −4x +3.
9.14. |
x = arccos y, |
|
|
|
|
x = 0, |
|||||||||
y = 0. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
9.16. |
y = x2 8 − x2 , y = 0, |
||||||||||||||
(0 ≤ x ≤ 2 |
|
|
|
|
). |
||||||||||
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||
9.18. |
y = x 4 − x2 , y = 0, |
||||||||||||||
(0 ≤ x ≤ 2). |
|
|
|
|
|
||||||||||
|
y = |
|
|
|
1 |
|
|
|
|
, |
|
y = 0, |
|||
9.20. |
1+cos x |
|
|||||||||||||
|
|
|
|
|
|
||||||||||
|
x =π 2, |
x = −π 2. |
|||||||||||||
9.22. |
y = cos5 xsin 2x, y = 0, |
||||||||||||||
(0 ≤ x ≤π 2). |
|
||||||||||||||
9.24. |
x = 4 − y2 , |
|
|
|
|
|
|
|
|
|
|||||
x = y2 −2y. |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||
9.26. |
y = e1 x |
, |
y = 0, |
||||||||||||
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
x = 2, |
x =1. |
|
||||||||||||
|
|
|
|
|
|
|
|
x = 0, |
|||||||
9.28. |
x = 4 − y2 , |
|
|
|
|
||||||||||
y = 0, |
y =1. |
|
|||||||||||||
|
|
||||||||||||||
9.30. |
y = x2 cos x, |
|
|
|
|
y = 0, |
|||||||||
(0 ≤ x ≤π 2). |
|
||||||||||||||

Задача 10. Вычислить длины дуг кривых, заданных уравнениями в прямоугольной системе координат.
10.1. y = ln x, |
|
|
3 |
≤ x ≤ |
15. |
|
|
||||||||
10.2. y = |
x2 |
|
− |
ln x |
, |
|
1 ≤ x ≤ 2. |
||||||||
4 |
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
10.3. y = |
|
|
|
|
|
0 ≤ x ≤ 7 9. |
|||||||||
1− x2 +arcsin x, |
|
||||||||||||||
10.3. y = ln |
5 |
, |
|
|
|
|
|
≤ x ≤ |
|
|
|||||
|
|
|
|
3 |
8. |
||||||||||
2x |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
10.5. y = −lncos x, |
|
0 ≤ x ≤π 6. |
|||||||||||||
10.6. y = ex +6, ln
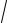 8 ≤ x ≤ ln
8 ≤ x ≤ ln 
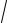 15.
15.
10.7. y = 2 +arcsin 
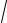 x +
x +
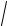 x − x2 , 1
x − x2 , 1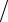 4 ≤ x ≤1.
4 ≤ x ≤1.
10.8. y = ln |
( |
x2 |
) |
|
−1 , 2 ≤ x ≤3. |
10.9. y = 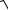
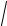 1− x2 +arccos x, 0 ≤ x ≤8
1− x2 +arccos x, 0 ≤ x ≤8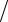 9.
9.
|
( |
|
|
|
) |
, |
|
0 ≤ x ≤1 4. |
|
|
|
|
|||||||||||
10.10. y = ln 1− x2 |
|
|
|
|
|
|
|||||||||||||||||
10.11. y = 2 +ch x, |
|
|
0 ≤ x ≤1. |
|
|
|
|
||||||||||||||||
10.12. y =1−lncos x, |
|
|
0 ≤ x ≤π 6. |
||||||||||||||||||||
10.13. y = ex +13, |
ln |
|
|
|
|
|
≤ x ≤ ln |
|
|
|
|
||||||||||||
15 |
24. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
10.14. y = −arccos |
|
|
|
+ |
|
|
x − x2 , |
0 ≤ x ≤1 4. |
|||||||||||||||
|
|
x |
|||||||||||||||||||||
10.15. y = 2 −ex , |
|
|
ln |
|
|
≤ x ≤ ln |
|
|
|||||||||||||||
|
|
|
3 |
8. |
|||||||||||||||||||
10.16. y = arcsin x − |
|
|
|
|
|
0 ≤ x ≤15 16. |
|||||||||||||||||
|
|
1− x2 , |
|
||||||||||||||||||||
10.17. y =1−lnsin x, |
) |
π 3 ≤ x ≤π 2. |
|||||||||||||||||||||
10.18. y =1 |
−ln |
( |
x2 |
|
|
|
|
|
|
3 ≤ x ≤ 4. |
|||||||||||||
|
−1 , |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
10.19. y = |
|
x − x2 −arccos |
|
+5, |
|
|
1 9 ≤ x ≤1. |
||||||||||||||||
|
x |
|
|
||||||||||||||||||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10.20. y = −arccos x + |
|
1− x2 +1, |
|
|
|
0 ≤ x ≤9 16. |
|||||||||||||||||
10.21. y = lnsin x, |
|
|
π 3 ≤ x ≤π 2. |
||||||||||||||||||||
10.22. y = ln7 −ln x, |
|
|
|
|
|
|
|
≤ x ≤ |
|
|
|
|
|
|
|||||||||
|
|
|
|
3 |
8. |
|
|
||||||||||||||||
10.23. y = ch x +3, |
|
|
0 ≤ x ≤1. |
|
|
|
|
|
|
||||||||||||||
10.24. y =1+arcsin x − |
|
|
|
|
|
|
|
|
0 ≤ x ≤3 4. |
||||||||||||||
|
|
|
1− x2 , |
|
|||||||||||||||||||
10.25. y = lncos x +2, |
|
|
0 ≤ x ≤π 6. |
||||||||||||||||||||
10.26. y = ex +26, |
|
ln |
|
|
|
≤ x ≤ ln |
|
|
|
|
|
||||||||||||
8 |
24. |
||||||||||||||||||||||
10.27. y = |
ex +e−x |
+3, |
|
|
|
0 ≤ x ≤ 2. |
|||||||||||||||||
|
2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
10.28. y = arccos |
|
|
− |
|
|
x − x2 +4, 0 ≤ x ≤1 2. |
|||||||||||||||||
|
x |
|
|
||||||||||||||||||||
10.29. y = |
ex +e−x +3 |
, |
|
|
|
0 ≤ x ≤ 2. |
|
|
|
|
|
|
|||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10.30. y = ex +e, |
ln |
|
≤ x ≤ ln |
|
|
|
|
||||||||||||||||
3 |
15. |
|
|||||||||||||||||||||
10.31. y = |
1−ex −e−x |
, |
|
|
|
0 ≤ x ≤3. |
|
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 11. Вычислить длины дуг кривых, заданных параметрическими |
|||||||||||||||||||||||
уравнениями. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x =5 |
(t −sint), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x =3(2cost −cos2t), |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.1. y =5(1−cost), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.2. y =3(2sint −sin 2t), |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 ≤t ≤π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 ≤t ≤ 2π. |
||||||
x = 4(cost +t sint),
11.3. y = 4(sint −t cost), 0 ≤t ≤ 2π.
x =(t2 −2)sint +2t cost,y =(2 −t2 )cost +2t sint,
0 ≤t ≤π.
t,
11.5.y =10sin3 t, 0 ≤t ≤π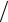 2.
2.
x =3(t −sint),
11.7.y =3(1−cost),
π≤t ≤ 2π.
x =3(cost +t sint),
11.9.y =3(sint −t cost),x =10cos3
0 ≤t ≤π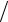 3.
3.
x =(t2 −2)sint +2t cost,y =(2 −t2 )cost +2t sint,
0 ≤t ≤π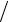 3.
3.
x = 6cos3 t,
11.11. y = 6sin3 t, 0 ≤t ≤π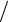 3.
3.
11.4.
x = et (cost +sint),
11.6. y = et (cost −sint), 0 ≤t ≤π.
x = 12 cost − 14 cos2t,
1 1
11.8. y = 2 sint − 4 sin 2t,
π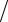 2 ≤t ≤ 2π
2 ≤t ≤ 2π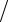 3.
3.
11.10.
+),
11.12.y = et (cost −sint),
π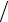 2 ≤t ≤π.x = et (cost sint
2 ≤t ≤π.x = et (cost sint
x = 2,5(t −sint),
11.13.y = 2,5(1−cost),
π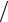 2 ≤t ≤π.
2 ≤t ≤π.
x =3,5(2cost −cos2t),
y =3,5(2sint −sin 2t),
0≤t ≤π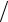 2.
2.
x = 6(cost +t sint),
11.15.y = 6(sint −t cost),
0 ≤t ≤π.
x =(t2 −2)sint +2t cost,y =(2 −t2 )cost +2t sint,
0 ≤t ≤π 2.
2.
x =8cos3 t,
11.17. y =8sin3 t,
0≤t ≤π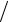 6.
6.
x = 4(t −sint),
11.19.y = 4(1−cost),
π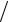 2 ≤t ≤ 2π
2 ≤t ≤ 2π 3.
3.
x = 2(2cost −cos2t),
y = 2(2sint −sin 2t), 0 ≤t ≤π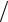 3.
3.
11.14.
11.16.
x = et (cost +sint),
11.18. y = et (cost −sint), 0 ≤t ≤ 2π.
11.20.

x =8(cost +t sint), |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
11.21. y =8 |
(sint −t cost), |
11.22. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 ≤t ≤π 4. |
|
|
|
|
|
|
|
|
||
x =(t2 −2)sint +2t cost, |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y =(2 −t2 )cost +2t sint, |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 ≤t ≤ 2π. |
|
|
|
|
|
|
|
|
||
|
|
3 |
|
|
x = e |
t |
( |
cost +sint |
) |
, |
||
|
|
|
|
|
||||||||
x = 4cos t, |
|
|
|
|
|
|
||||||
|
|
|
|
11.24. |
|
y = et (cost −sint), |
||||||
11.23. y = 4sin3 t, |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
π 6 ≤t ≤π 4. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
0 ≤t ≤3π 2. |
||||||||
x = 2 |
(t −sint), |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
11.25. y = 2 |
(1−cost), |
11.26. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 ≤t ≤π 2. |
|
|
|
|
|
|
|
|
|||
x = 4 |
(2cost −cos2t), |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
y = 4 |
(2sint −sin 2t), |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 ≤t ≤π. |
|
|
|
|
|
|
|
|
||
x = 2 |
(cost +t sint), |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
11.27. y = 2 |
(sint −t cost), |
11.28. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 ≤t ≤π 2. |
|
|
|
|
|
|
|
|
||
x =(t2 −2)sint +2t cost, |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y =(2 −t2 )cost +2t sint, |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 ≤t ≤3π. |
|
x = e |
|
|
cost +sint |
|
, |
||||
|
3 |
|
|
t |
( |
) |
||||||
x = 2cos |
t, |
|
|
|
|
|
||||||
|
|
|
|
|
|
|||||||
|
|
|
|
11.30. |
|
y = et (cost −sint), |
||||||
11.29. y = 2sin3 t, |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
0 ≤t ≤π 4. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
π 6 ≤t ≤π 4. |
||||||||

x =(t2 −2)sint +2t cost,
11.31.y =(2 −t2 )cost +2t sint,
0 ≤t ≤π.
Задача 12. Вычислить длины дуг кривых, заданных уравнениями в полярных координатах.
12.1.ρ =3e3ϕ 4 , −π
4 , −π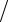 2 ≤ϕ ≤π
2 ≤ϕ ≤π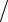 2.
2.
12.2.ρ = 2e4ϕ 3 , −π
3 , −π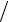 2 ≤ϕ ≤π
2 ≤ϕ ≤π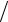 2.
2.
12.3.ρ = 
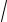 2 eϕ , −π
2 eϕ , −π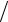 2 ≤ϕ ≤π
2 ≤ϕ ≤π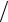 2.
2.
12.4.ρ =5e5ϕ 12 , −π
12 , −π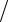 2 ≤ϕ ≤π
2 ≤ϕ ≤π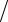 2.
2.
12.5.ρ = 6e12ϕ 5 , −π
5 , −π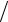 2 ≤ϕ ≤π
2 ≤ϕ ≤π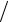 2.
2.
12.6. ρ =3e3ϕ 4 , |
0 ≤ϕ ≤π 3. |
|||||
12.7. ρ = 4e4ϕ 3 , |
0 ≤ϕ ≤π 3. |
|||||
12.8. ρ = |
|
eϕ , |
0 ≤ϕ ≤π 3. |
|||
2 |
||||||
12.9. ρ =5e5ϕ 12 , |
0 ≤ϕ ≤π 3. |
|||||
12.10. ρ =12e12ϕ 5 , |
0 ≤ϕ ≤π 3. |
|||||
12.11. ρ =1−sinϕ, |
−π 2 ≤ϕ ≤ −π 6. |
|||||
12.12. ρ = 2 |
(1−cosϕ), |
−π ≤ϕ ≤ −π 2. |
||||
12.13. ρ =3(1+sinϕ), |
−π 6 ≤ϕ ≤ 0. |
|||||
12.14. ρ = 4 |
(1−sinϕ), |
0 ≤ϕ ≤π 6. |
||||
12.15. ρ =5 |
(1−cosϕ), |
−π 3 ≤ϕ ≤ 0. |
||||
12.16. ρ = 6 |
(1+sinϕ), |
−π 2 ≤ϕ ≤ 0. |
||||
12.17. ρ = 7 |
(1−sinϕ), |
−π 6 ≤ϕ ≤π 6. |
||||
12.18. ρ =8 |
(1−cosϕ), |
−2π 3 ≤ϕ ≤ 0. |
||||

12.19.ρ = 2ϕ, 0 ≤ϕ ≤3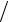 4.
4.
12.20.ρ = 2ϕ, 0 ≤ϕ ≤ 4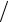 3.
3.
12.21.ρ = 2ϕ, 0 ≤ϕ ≤5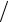 12.
12.
12.22.ρ = 2ϕ, 0 ≤ϕ ≤12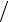 5.
5.
12.23.ρ = 4ϕ, 0 ≤ϕ ≤3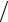 4.
4.
12.24.ρ =3ϕ, 0 ≤ϕ ≤ 4 3.
3.
12.25.ρ =5ϕ, 0 ≤ϕ ≤12 5.
5.
12.26. ρ = 2cosϕ, |
0 ≤ϕ ≤π 6. |
12.27. ρ =8cosϕ, |
0 ≤ϕ ≤π 4. |
12.28. ρ = 6cosϕ, |
0 ≤ϕ ≤π 3. |
12.29. ρ = 2sinϕ, |
0 ≤ϕ ≤π 6. |
12.30. ρ =8sinϕ, |
0 ≤ϕ ≤π 4. |
12.31. ρ = 6sinϕ, |
0 ≤ϕ ≤π 3. |
Задача 13. Вычислить объемы тел, образованных вращением фигур, ограниченных графиками функций. В вариантах 1–16 ось вращения Ox , в вариантах 17–31 ось вращения Oy .
13.1. y = −x2 +5x −6, |
y = 0. |
||||
13.2. 2x − x2 − y = 0, 2x2 −4x + y = 0. |
|||||
13.3. y =3sin x, |
|
y =sin x, |
0 ≤ x ≤π. |
||
13.4. y =5cos x, |
y = cos x, |
x = 0, x ≥ 0. |
|||
13.5. y =sin2 x, |
x =π 2, |
y = 0. |
|||
13.6. x = 3 |
|
|
x =1, |
y =1. |
|
y −2, |
|||||
13.7. y = xex , |
y = 0, |
x =1. |
|||
13.8. y = 2x − x2 , |
y = −x +2, x = 0. |
||||
13.9. y = 2x − x2 , |
y = −x +2. |
||||
13.10. y = e1−x , y = 0, x = 0, x =1.
13.11.y = x2 , y2 − x = 0.
13.12.x2 +(y −2)2 =1.
|
y =1− x2 , |
x = 0, |
x = |
|
|
|
x =1. |
|||||||
13.13. |
|
y −2, |
||||||||||||
13.14. |
y = x2 , |
y =1, |
|
x = 2. |
|
|
|
|
|
|||||
|
y = x3 , |
y = |
|
|
. |
|
|
|
|
|
|
|
||
13.15. |
|
x |
|
|
|
|
|
|
|
|||||
13.16. |
y =sin(πx 2), |
y = x2. |
|
|
|
|
|
|||||||
13.17. |
y = arccos(x 3), |
y = arccos x, |
y = 0. |
|||||||||||
13.18. |
y = arcsin(x 5), |
y = arcsin x, |
y =π 2. |
|||||||||||
13.19. |
y = x2 , |
x = 2, |
y = 0. |
|
|
|
|
|
||||||
13.20. |
y = x2 +1, |
y = x, |
x = 0, |
y = 0. |
||||||||||
|
y = |
|
|
y = 0, |
y =1, |
x = 0,5. |
||||||||
13.21. |
x −1, |
|||||||||||||
13.22. |
y = ln x, |
|
x = 2, |
y = 0. |
|
|
|
|
|
|||||
13.23. |
y =(x −1)2 , |
|
y =1. |
|
|
|
|
|
|
|||||
13.24. |
y2 = x −2, |
y = 0, |
y = x3 , |
y =1. |
||||||||||
13.25. |
y = x3 , |
y = x2. |
|
|
|
|
|
|
|
|||||
13.26. |
y = arccos(x 5), |
y = arccos(x 3), y = 0. |
||||||||||||
13.27. |
y = arcsin x, |
|
y = arccos x, |
y = 0. |
||||||||||
13.28. |
y = x2 −2x +1, |
x = 2, |
y = 0. |
|
||||||||||
13.29. |
y = x3 , |
y = x. |
|
|
|
|
|
|
|
|||||
13.30. |
y = arccos x, |
y = arcsin x, |
x = 0. |
|||||||||||
13.31. |
y =(x −1)2 , |
|
x = 0, |
x = 2, |
y = 0. |
|||||||||
