
Kurpa_Vyshcha_matem_T.2_Gl.9-12_2009
.pdf
Знайдемо масу дуги m (x, y, z)dl . Відповідно до умови
L
(x, y, z) kxy .
dl |
2 |
|
|
2 |
|
2 |
dt |
|
a |
2 |
sin |
2 |
|
t a |
2 |
|
|
cos |
2 |
t b |
2 |
dt |
|
|
|
a |
2 |
b |
2 |
dt ; |
|||||||||||||||||||||||||
xt |
yt |
zt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
m kxy |
|
a 2 b2 dt k |
|
|
|
|
a2 b2 |
a 2 cost sin tdt |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2 t |
|
|
|
|
|
a 2k |
|
|
a 2 b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
a 2k a 2 |
b |
2 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ka3 |
|
|
|
|
a 2 b2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x (x, y, z)dl ka3 |
|
a 2 b2 |
|
cos2 t sin tdt |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ka3 |
|
|
|
|
a 2 b2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
y (x, y, z)dl ka3 |
|
a 2 b2 |
|
sin 2 t costdt |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z (x, y, z)dl kba2 |
|
|
|
a 2 b2 t sin t costdt |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
a 2bk a 2 b2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
a 2bk a 2 |
b2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t sin 2tdt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
x |
c |
|
2a |
|
|
, y |
c |
|
2a |
, z |
c |
|
b |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
11.2.Криволінійні інтеграли II роду
1.Нехай L – кусково-гладка просторова крива, на якій задано напрямок, а P(x, y, z) , Q(x, y, z) , R(x, y, z) – неперервні функції, які
визначені на ній. Розіб'ємо криву L на елементарні ділянки Ai1 Ai , проекції яких на координатні осі Ox, Oy, Oz відповідно позначимо xi xi xi 1,
yi yi yi1 , zi zi zi1 . Виберемо на кожній з ділянок довільну точку Mi ( i , i , i ) і обчислимо значення функції в цій точці.
Утворимо суму
121

n
Wn P(M i ) xi Q(M i) yi R Mi zi ,
i 1
яка називається інтегральною сумою по координатах.
Визначення. Якщо max Ai 1 Ai прямує до нуля і ця сума має скінчену границю W, що не залежить від способу розбиття кривої та вибору точок Mi, то ця границя називається криволінійним інтегралом II роду вздовж кривої L і позначається як
W P(x, y, z)dx Q(x, y, z)dy R(x, y, z)dz .
L
Криволінійний інтеграл II роду залежить від вибору напрямку кривої. При зміні напрямку інтеграл змінює знак, тобто
Pdx Qdy Rdz Pdx Qdy Rdz .
AB |
|
|
BA |
За своїм фізичним змістом |
криволінійний інтеграл II роду являє |
||
собою роботу змінної сили |
|
P,Q, R , точка прикладення якої описує |
|
F |
|||
криву L.
2. Обчислення криволінійного інтеграла II роду зводиться до
обчислення визначеного інтеграла. |
|
||
а) |
Якщо плоска крива задана рівнянням y y(x), x a,b , причому |
||
початку кривої відповідає x a , а кінцю – x b , то |
|||
|
|
b |
|
|
|
|
|
|
P(x, y)dx Q(x, y)dy P[x, y(x)]dx Q[x, y(x)]yx dx . |
||
|
L |
a |
|
б) |
Якщо крива |
L задана параметрично і початковій точці кривої |
|
відповідає значення параметра t t1 , а кінцевій точці – t t2 |
|||
|
|
x x(t) |
, t t1,t2 , |
|
|
|
|
|
|
y y(t) |
|
то |
|
|
|
|
|
t2 |
|
|
P(x, y)dx Q(x, y)dy P[x(t), y(t)]xt dt Q[x(t), y(t)]yt dt . |
||
|
L |
t1 |
|
Зверніть увагу, що і у випадку a) і у випадку б) нижня межа інтеграла необов'язково менша за верхню.
122

Визначення 1. Область D R2 називається однозв’язною, якщо для
будь-якого замкненого контуру |
L D |
|
область, яка обмежена цим |
|||||
контуром, також цілком лежить в плоскості D . |
|
|
|
|||||
Визначення 2. Область |
G R3 |
називається |
поверхнево- |
|||||
однозв’язною або однозв'язною, якщо на |
будь-який замкнений контур |
|||||||
L G можна натягнути поверхню, що цілком лежить в області G . |
||||||||
Теорема. Якщо функції P x, y і |
Q x, y та їх частинні похідні |
|||||||
першого порядку неперервні в замкненій однозв'язній області |
D R2 , яка |
|||||||
обмежена кусково-гладкою додатно орієнтованою кривою |
L , то має |
|||||||
місце формула |
|
|
|
|
|
|
|
|
|
P x, y dx Q x, y |
dy |
|
|
Q |
P |
|
(11.1) |
|
dxdy . |
|||||||
|
|
|
x |
y |
|
|
||
L |
|
|
D |
|
|
|
||
|
|
|
|
|
|
|
||
Формула (11.1) називається формулою Гріна.
Формулу Гріна можна розповсюдити на будь-яку область, яку можна розбити на скінченне число областей вказаного в теоремі типу (наприклад, область, що має точки самоперетину, область, що не є однозв'язною).
Теорема 1. Нехай функції P x, y |
і Q x, y та їх частинні похідні P |
|||
|
|
|
|
y |
і Q неперервні в замкненій |
однозв'язній області D . Тоді |
має місце |
||
x |
|
|
|
|
рівносильність таких чотирьох тверджень: |
|
|||
1. |
Pdx Qdy 0 , |
|
|
|
|
L |
|
|
|
де L – будь-який замкнений контур, що лежить в області D . |
|
|||
2. |
Pdx Qdy не залежить від форми шляху, що з'єднує точки A і |
|||
|
AB |
|
|
|
B , AB D . |
|
|
|
|
3. |
Pdx Qdy du x, y , |
тобто |
вираз Pdx Qdy |
є повним |
диференціалом деякої функції u x, y , визначеної в області D . |
|
|||
4. У всіх точках області D |
|
|
|
|
|
|
Q |
P . |
(11.2) |
|
|
x |
y |
|
При виконанні умов цієї теореми, як наслідок, має місце формула
123

P x, y dx Q x, y dy |
du x, y u B u A u x, y |
|
BA . (11.3) |
|
|||
|
|||
AB |
AB |
||
Аналогічна теорема має місце для тривимірного випадку. |
|||
Теорема 2. Нехай функції |
P x, y,z , Q x, y,z , R x, y,z неперервні |
||
разом зі своїми частинними похідними першого порядку в замкненій поверхнево-однозв'язній області G . Тоді має місце рівносильність таких чотирьох тверджень:
1. |
Pdx Qdy Rdz 0 , |
|
|
L |
|
де L – будь-який замкнений контур, що лежить в області G . |
||
2. |
Pdx Qdy Rdz не залежить від форми шляху, що з'єднує точки |
|
|
AB |
|
A і B , |
AB G . |
|
3. |
Pdx Qdy Rdz du x, y,z , тобто вираз |
Pdx Qdy Rdz є |
повним диференціалом деякої функції u x, y,z , визначеної в області G .
4. У всіх точках області G виконуються рівності |
|
||||||||
Q |
P , |
R |
Q |
, |
P |
R |
(11.4) |
||
x |
y |
y |
z |
|
z |
x |
|
||
При виконанні умов цієї теореми, як наслідок, має місце формула: |
|||||||||
Pdx Qdy Rdz du x, y,z u B u A u x, y,z |
|
BA . |
(11.5) |
||||||
|
|||||||||
|
|
||||||||
AB |
AB |
|
|
|
|
|
|
|
|
Знаходження функції за її повним диференціалом |
|
||||||||
За допомогою розглянутих теорем можна розв'язати таку задачу. |
|||||||||
Нехай відомо, що вираз Pdx Qdy |
є повним диференціалом деякої |
||||||||
функції u x, y , тобто Pdx Qdy du x, y . Умовою того, що цей вираз є
повним диференціалом, є виконання умови (4.16):
цю функцію u x, y .
Розв'язання задачі виконується так: з виразу
du Pdx Qdy
випливає, що |
x,y |
|
u x, y |
||
Pdx Qdy , |
||
|
x0 ,y0 |
Q P . Треба знайти
x y
124
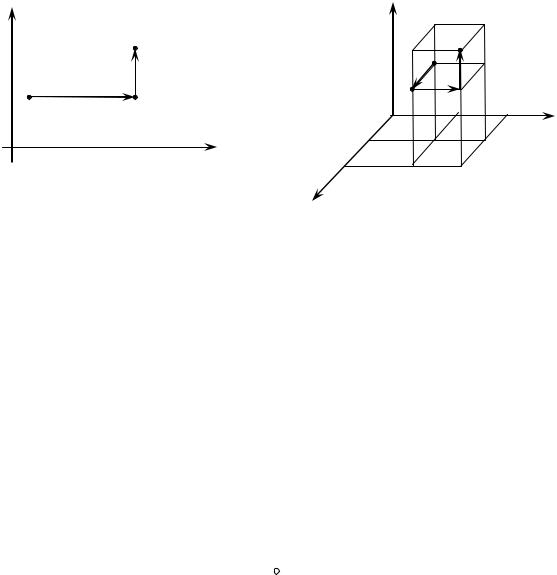
M0 x0 , y0 , M x, y D , D – область визначення функцій P x, y , і криволінійний інтеграл не залежить від форми шляху інтегрування, а тільки від початкової та кінцевої точок цього шляху. Цей шлях вибираємо, як правило, у вигляді ламаної, складеної з відрізків прямих, паралельних осям координат. Отже, формула для знаходження
функції за її повним диференціалом буде подана так:
x |
y |
|
|
u x, y P x, y0 |
dx Q x, y dy C , |
|
|
x0 |
y0 |
x0 , y0 |
, |
де M 0M – ламана (рис. 11.3), яка з'єднує точки M0 |
|||
що відрізки ламаної паралельні осям координат. |
|
|
|
y |
z |
|
|
M x, y |
M |
M 0 |
M 0 x0 , y0 |
M1 x1, y1 |
0 |
y0 |
|
|
x0 |
|
|
|
|
(11.6)
M x, y так,
y y
0 |
x |
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
Рис. 11.3 |
|
|
Рис. 11.4 |
|
|
||
Аналогічно розглядається поставлена задача для тривимірного |
|||||||
випадку. |
|
|
|
|
|
|
|
Якщо виконуються умови (4.18): |
Q |
P , |
R |
Q , |
P |
R , то |
|
|
|
x |
y |
y |
z |
z |
x |
P x, y,z dx Q x, y,z dy R x, y,z dz du x, y,z і тоді |
|
|
|
||||
x |
y |
|
|
y |
|
|
|
u x, y P x, y0 ,z0 dx Q x, y,z0 dy |
R x, y,z dz C , (11.7) |
||||||
x0 |
y0 |
|
|
y0 |
|
|
M x, y,z |
де M 0M – ламана (рис. |
11.4), яка з'єднує точки M0 x0 , y0 ,z0 , |
||||||
так, що сторони ламаної паралельні осям координат.
Застосування криволінійного інтеграла II роду.
а) Площа плоскої фігури, що обмежена замкнутою кривою L обчислюється за формулою
S xdy .
L
125

б) Робота змінної сили F(P,Q, R) при переміщенні матеріальної точки вздовж дуги L обчислюється так:
W Pdx Qdy Rdz .
L
11.2.1. Приклади обчислення криволінійних інтегралів II роду
Приклад 1. Обчислити x 2 dx |
dy |
|
, де |
L – дуга кривої |
x |
1 |
від |
|||||||||||||||||||||||||||||||||||||||||||||||
y 2 |
y |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
точки A(4, 1 |
) до |
B(1,1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Розв’язання. З рівняння кривої |
y x , y |
x2 . |
|
Змінна х відіграє |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
роль параметра. Початковій точці кривої відповідає x 4, кінцевій – |
x 1. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
dy |
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x2dx |
|
x2dx |
|
(x2 )dx (x2 1)dx 18 . |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
y 2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
L |
|
|
|
4 |
|
|
|
|
|
x2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Приклад 2. Обчислити ydx xdy , де L – дуга астроіди x a cos3 t , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y a sin3 t , що розташована між тачками A a,0 та |
|
|
|
a |
|
|
|
|
|
a |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
B |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
. |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
2 |
2 |
|
|
|
|
|
|||||||||
Розв’язання. Знайдемо dx 3a sin t cos2 tdt , |
|
dy 3a sin 2 t costdt , |
||||||||||||||||||||||||||||||||||||||||||||||||||||
ydx xdy 3a2 sin 4 t cos2 tdt 3a2 cos4 t sin 2 tdt |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
2 |
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3a |
|
sin |
|
|
t cos |
|
t(cos t sin |
|
|
|
t)dt |
|
|
|
a |
|
|
sin |
|
|
2t cos2tdt. |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Початковій точці дуги відповідає t 0 , кінцевій – |
t |
|
|
, тоді |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 3 2t |
|
|
|
|
|
|
|
|
a 2 |
|
|
|
||||||||||||||
ydx xdy |
3 |
a 2 |
4 sin 2 |
2t cos2tdt |
3 |
a 2 |
|
|
|
4 |
|
. |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
L |
|
|
|
|
|
4 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
3 |
|
|
|
0 |
|
|
|
|
|
8 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Приклад 3. |
Обчислити y 2dx (x2 z)dy (x y z 2 )dz , де |
L – |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
відрізок прямої в просторі від точки A(1,0,2) до B(3,1,4) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Розв’язання. Складемо рівняння прямої, що проходить через точки |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
A і B : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
y |
|
|
z 2 |
|
t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
126

Введемо параметр t і одержимо:
x 2t 1, dx 2dt, y t, dy dt,
z 2t 2, dz 2dt.
Параметр змінюється в межах t A t tB , тобто 0 t 1 .
y 2dx (x2 z)dy (x y z 2 )dz
L
1 |
|
|
|
|
|
2t 2dt (1 2t)2 2t 2 dt (2t 1) t (2t 2)2 dt |
|||||
0 |
|
|
|
|
|
1 |
|
95 |
|
|
|
(14t 2 28t 13)dt |
. |
|
|
||
|
|
|
|||
0 |
3 |
|
|
|
|
|
|
|
|
F y2 z2 ; x; yz |
|
Приклад 4. Знайти роботу, що |
виконує |
сила |
|||
вздовж дуги гіперболічної гвинтової |
лінії x bt; y a cht; z a sht від |
||||
точки A 0, a,0 до точки B b, ach1, ash1 . |
|
|
|
|
|
Розв’язання. Робота дорівнює |
|
|
|
|
|
W P(x, y, z)dx Q(x, y, z)dy R(x, y, z)dz ( y 2 |
z 2 )dx xdy yzdz . |
||||
L |
L |
|
|
||
Використовуючи рівняння кривої, знайдемо: |
|
|
|||
dx bdt;dy a shtdt;dz a chtdt . |
|
|
|
|
|
Початковій точці дуги відповідає t 0 , кінцевій – |
t 1, тоді |
||||
1 |
|
|
|
1 |
1 |
W a 2 (ch2 t sh2 t)bdt bta shtdt a3 ch2 t sh tdt a 2bdt ab t sh tdt
|
|
0 |
|
|
|
|
|
0 |
|
0 |
|
|
|||||||
|
|
1 |
|
|
|
|
a3 |
|
|
|
|
|
|
|
|
|
|
|
|
a3 ch2 t sh tdt a 2b ab(ch1 sh1) |
|
(ch3 1 1). |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
0 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Приклад 5. Знайти площу еліпса |
x2 |
|
|
y 2 |
1. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
a2 |
|
|
b2 |
|
|
|
|
|
||||
|
|
Розв’язання. |
Перейдемо |
|
|
до |
|
|
параметричних |
|
|
|
рівнянь |
||||||
x a cost; y bsin t . |
Додатному |
обходу контуру |
відповідає |
зміна |
|||||||||||||||
параметра t від 0 до 2 , тоді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
1 |
2 |
|
|
|
|
|
|
|
1 |
|
2 |
ab |
|
|
|
|
S |
xdy ydx |
a costb costdt b sin ta sin tdt |
ab dt |
|
2 ab . |
||||||||||||||
|
|
|
|
||||||||||||||||
2 |
L |
2 |
0 |
|
|
|
2 |
|
0 |
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
127

Приклад 6. Перевірити, що даний вираз (1 sin 2x)dy (3 2y cos2x)dx є повним диференціалом функції u(x, y) , та знайти цю функцію.
Розв’язання. |
(1 sin 2x)dy (3 2y cos2x)dx P(x, y)dx Q(x, y)dy . |
||||||
Знайдемо P |
2 cos2x; |
Q 2 cos2x . |
|
|
|
||
|
y |
|
|
x |
|
|
|
Якщо |
P |
Q , |
то |
вираз P(x, y)dx Q(x, y)dy |
є повним |
||
|
y |
x |
|
|
|
|
|
диференціалом функції |
u(x, y) . Знайдемо |
цю |
функцію, |
приймаючи |
|||
x0 0; y0 0 . |
|
|
|
|
|
|
|
|
x |
|
y |
|
x |
y |
|
u(x, y) P(x, y0 )dx Q(x, y)dy C |
3dx (1 sin 2x)dy C |
||||||
|
x0 |
|
y0 |
|
0 |
0 |
|
3x (1 sin 2x) y C.
Приклад 7. Обчислити |
x2 ydx xy 2dy , |
де |
L – |
додатно |
||||||
|
|
L |
|
|
|
|
|
|
|
|
орієнтоване коло x2 y 2 a 2 . |
|
|
|
|
|
|
|
|
|
|
Розв’язання. У задачі |
|
|
|
|
|
|
|
|
|
|
P(x, y) x2 y;Q(x, y) xy 2 , |
P |
x2 ; |
Q y 2 . |
|
|
|||||
|
|
y |
|
|
|
x |
|
|
|
|
|
P Q |
|
|
|
|
|
|
|
|
|
Функції P(x, y),Q(x, y), y , |
x |
|
неперервні |
в |
області |
D , яка |
||||
обмежена колом L , тому, застосовуючи формулу Гріна, одержимо |
|
|||||||||
|
Pdx Qdy |
|
|
Q |
P |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
dxdy, |
|
|
|||||
L |
|
|
D |
|
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x2 ydx xy 2dy y 2 x2 dxdy . |
|
|||||||||
L |
|
|
|
|
D |
|
|
|
|
|
Уподвійному інтегралі перейдемо до полярних координат. Тоді
xcos ,
y sin ,
x2 y 2 a 2 2 .
|
|
2 |
a |
a 4 |
|
|
|
x2 |
y 2 dxdy 2 d d |
d 3d |
2 |
a 4 . |
|||
4 |
|||||||
D |
D |
0 |
0 |
|
2 |
||
|
|
|
|||||
128

|
|
Приклад 8. Знайти функцію за повним диференціалом. |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
du |
2 zxdy xydz yzdx |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
x yz 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Розв’язання. Для знаходження u x, y, z будемо інтегрувати цей |
|||||||||||||||||||||||||||||||||||
вираз |
по ламаній |
M 0 ABM (рис. |
11.3), |
|
|
відрізки |
якої |
|
паралельні |
||||||||||||||||||||||||||||
координатним осям, вибравши початкову точку M 0 1,0,0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
z |
|
|
|
|
|
|
|
|
u x, y, z |
|
|
du du du |
du . |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M0M |
M0 A |
|
|
|
|
AB |
BM |
||||||||||
|
|
M(x,y,z) |
|
|
|
|
|
|
|
Обчислимо кожен інтеграл окремо. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
y |
|
|
Рівняння лінії M0 A : y 0, z 0 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 zxdy |
xydz yzdx |
|
|
|
|
|||||||||||||||||
M0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0. |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x yz 2 |
|
|
|
|
|
|
|
||||||||||||||
A |
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
M 0 A |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
Рівняння лінії AB : x const,z 0 |
|||||||||||||||||||||||||||
|
|
Рис. 11.5 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 zxdy xydz yzdx |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0. |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x yz 2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рівняння лінії BM : x const, y const |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 zxdy xydz yzdx |
z |
|
xydz |
|
|
|
|
|
|
|
z |
d x yz |
|
2x |
|
|
|
|
z |
|
|
2x |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C.. |
||||||
|
x yz 2 |
x yz 2 |
x yz 2 |
x yz |
|
0 |
|
x yz |
|||||||||||||||||||||||||||||
BM |
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
u x, y, z |
|
|
2x |
|
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
x yz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
Приклад 9. Розглянемо |
|
ydx xdy , де L – довільний замкнений |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 y 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
контур. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Розв’язання. Підінтегральна функція має розрив у точці О(0,0). |
|||||||||||||||||||||||||||||||||||
|
|
|
|
P x, y |
|
|
y |
|
|
|
|
|
|
P |
|
|
y 2 x2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
; |
|
y |
|
|
|
, |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
x2 y 2 |
|
|
x2 y 2 2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
Q x, y |
|
x |
|
; |
|
|
Q |
|
|
|
|
y 2 x2 |
|
|
|
Q |
|
|
|
P |
, |
|
|||||||||||||
|
|
x2 y 2 |
|
|
x |
|
x2 y 2 2 |
|
|
x |
|
|
y |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
тобто підінтегральний вираз є повним диференціалом у будь-якій області, що не містить точку О(0,0).
Якщо ця точка не входить до області, що обмежена замкнутим контуром L, то інтеграл дорівнює нулю. Якщо ж точка О(0,0) перебуває
129

усередині області, що обмежена контуром L, то застосувати формулу Гріна не можна. Обчислимо криволінійний інтеграл безпосередньо. Нехай L – будь-який замкнутий контур, що містить точку О(0,0). Перейдемо до полярних координат
x cos , |
dx cos d sin d , |
|
|
y sin , |
dy sin d cos d , |
|
x2 y2 2 . |
xdy ydx cos sin d cos d sin cos d sin d2 cos2 d 2 sin 2 d 2 cos2 sin 2 d 2d
|
|
|
ydx xdy |
2 2d |
2 |
|||||
|
|
x |
2 |
y |
2 |
|
|
2 |
d 2 . |
|
|
|
L |
|
|
0 |
|
0 |
|||
|
|
|
|
|
|
|
|
|||
|
ydx xdy |
2 , |
якщо точка О(0,0) вcередині контуру L, |
|||||||
|
|
|
|
|
|
|
|
|||
x2 y2 |
0, |
|
якщо точка О(0,0) поза контуром L. |
|||||||
L |
|
|
|
|
|
|
|
|
|
|
11.3. Поверхневі інтеграли
11.3.1. Поверхневі інтеграли I роду
Визначення. Поверхня називається гладкою, якщо в кожній її точці існує дотична площина і при переході від точки до точки положення цієї дотичної площини змінюється неперервно. Поверхня, яка складається із скінченного числа неперервно сполучених гладких поверхонь, називається
кусково-гладкою.
Нехай дана функція f (x, y, z) неперервна на деякій гладкій поверхні. Розіб'ємо поверхню довільно проведеними кривими на ряд елементарних підобластей 1, 2 ,..., n . У кожній із цих частин i виберемо довільну точку M i (xi , yi , zi ) , обчислимо значення даної функції в цій точці й помножимо його на площу i . Утворимо суму всіх таких добутків
n
Tn f (xi , yi , zi ) i ,
i 1
яка називається інтегральною сумою. Позначимо через d i діаметр елементарної частини поверхні, тобто відстань між її найбільш вилученими точками.
130
