
Лекції 2013-2014
.pdfМинистерство образования и науки Украины
Конспект лекций
по курсу
«Компьютерная логика»
Богомаз Александр Викторович
Харьков 2013
«Компьютерная логика»
1семестр
1.Цели и задачи курса. Основные определения.
2.Информационные основы компьютерной техники.
3.Логические функции.
4.Логические элементы. Их обозначение и классификация.
5.Реализация логических элементов (с помощью релейно-контактных схем, на диодах и транзисторах, логические микросхемы, другие реализации).
6.Комбинационные схемы.
7.Методы минимизации переключающих функций.
8.Синтез комбинационных схем в разных элементных базисах.
2семестр
1.Комбинационные схемы в компьютерной технике.
2.Основы теории цифровых автоматов с памятью.
3.Методы синтеза цифровых автоматов с памятью.
4.Анализ логических схем и динамических процессов в цифровых автоматах.
5.Типичные цифровые схемы компьютеров.
Литература
1.Айзерман М.А., Гусев Л.А. и др. Логика. Автоматы. Алгоритмы. – М.: Физматгиз, 1963. – 556 с.
2.Пухальский Г.И., Новосельцева Т.Я. Проектирование дискретных устройств на интегральных микросхемах: Справочник. – М. : Радио и связь, 1990. – 304 с.
3.Шоломов Л.А. Основы теории дискретных логических и вычислительных устройств. – М. : Наука. Главная редакция физикоматематической литературы, 1980. – 400 с.
4.Точчи Р.Дж., Уидмер Н.С. Цифровые системы. Теория и практика, 8-е издание. : Пер. с англ. – М. : Издательский дом «Вильямс»,
2004. – 1024 с.

Лекция 1 Цели и задачи курса. Основные определения
Понятие логики Логика – это наука о законах и формах мышления.
Логика – раздел философии, наука о формах, методах и законах познавательной деятельности, формализуемых с помощью логического языка.
Логика возникла в Китае, Индии и Древней Греции примерно в IV в до н. э. Современная логика происходит из греческой, основателем которой считают Аристотеля.
Слово «логика» используется также в значениях «внутренняя закономерность, присущая тем или иным явлениям».
Алгебра логики (алгебра высказываний) – раздел математической логики, изучающий строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.
Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Еѐ создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.
Таким образом, алгебра логики (другое название - Булева алгебра) - это область математики. Она оперирует величинами, которые могут принимать два значения (булевых значения). Эти два значения могут быть обозначены как угодно, лишь бы по-разному. Самые распространенные варианты:
0, 1 F, T
false, true
ложь, истина Л, И
Алгебра логики применяется: 1) для упрощения сложных логических формул и доказательств тождеств; 2) при решении логических задач; 3) в
контактных схемах; 4) при доказательствах теорем; 5) в базах данных при составлении запросов.
Логическое высказывание – утверждение, которому всегда можно поставить в соответствие одно из двух логических значений ложь (0, ложно, false) или истина (1, истинно, true). Логическое высказывание принято обозначать заглавными латинскими буквами. Высказывательной формой называется логическое высказывание, в котором один из объектов заменѐн переменной. При подстановке вместо переменной какого-либо значения высказывательная форма превращается в высказывание.
Пример: A(x) = «В городе x идет дождь» A – высказывательная форма, x – объект.
Отрицание логического высказывания – логическое высказывание, принимающее значение «истинно», если исходное высказывание ложно, и наоборот.
Конъюнкция двух логических высказываний – логическое высказывание, истинное только тогда, когда они одновременно истинны.
Дизъюнкция двух логических высказываний – логическое высказывание, истинное только тогда, когда хотя бы одно из них истинно.
Импликация двух логических высказываний – логическое высказывание, ложное только тогда, когда одно из них ложно, а другое – истинно.
Равносильность (эквивалентность) двух логических высказываний – логическое высказывание, истинное только тогда, когда они одновременно истинны или ложны.
Кванторное логическое высказывание с квантором всеобщности
(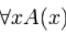 ) – логическое высказывание, истинное только тогда, когда для каждого объекта x из заданной совокупности высказывание A(x) истинно.
) – логическое высказывание, истинное только тогда, когда для каждого объекта x из заданной совокупности высказывание A(x) истинно.
Кванторное логическое высказывание с квантором существования
(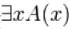 ) – логическое высказывание, истинное только тогда, когда в заданной совокупности существует объект x, такой, что высказывание A(x) истинно.
) – логическое высказывание, истинное только тогда, когда в заданной совокупности существует объект x, такой, что высказывание A(x) истинно.
Высказывание (суждение) – некоторое предложение, которое может быть истинно (верно) или ложно
Утверждение – суждение, которое требуется доказать или опровергнуть.
Рассуждение – цепочка высказываний или утверждений, определенным образом связанных друг с другом
Умозаключение – логическая операция, в результате которой из одного или нескольких данных суждений получается (выводится) новое суждение
Логическое выражение – запись или устное утверждение, в которое, наряду с постоянными, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных логическое выражение может принимать одно из двух возможных значений: ИСТИНА (логическая 1) или ЛОЖЬ (логический 0).
Сложное логическое выражение – логическое выражение,
составленное из одного или нескольких простых (или сложных) логических выражений, связанных с помощью логических операций.
Лекция 2 Информационные основы компьютерной техники
Числа – абстрактная сущность, используемая для описания количества, сравнения и нумерации объектов.
Цифры – система знаков для записи чисел.
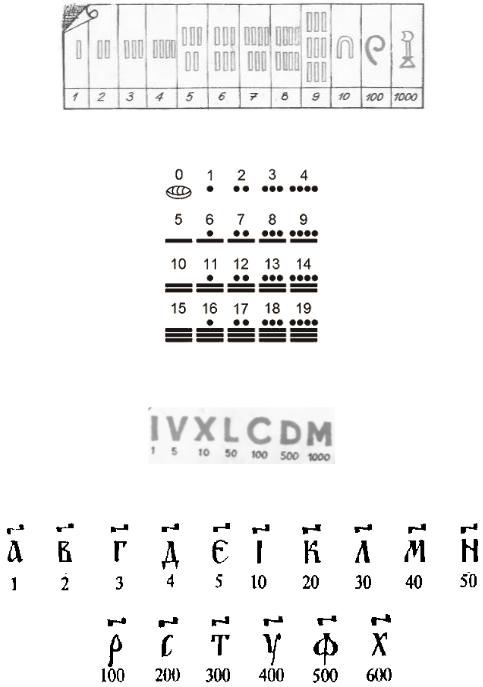
Цифры в древнем мире:
Египет
Майа
Рим
Старославянские
Система счисления – совокупность правил записи чисел.
Наиболее часто используются позиционные системы счисления, в которой положительное целое число записывается в виде последовательности символов enen–1..ep..e2e1, а вес каждого символа ep определяется его позицией в записи числа. Вес символа ep равен qp–1, q – основание системы счисления, а ep=0, 1, ..., q–1. Тогда любое целое положительное число E в системе счисления с основанием q можно записать
n
в виде E = ep q p 1 . При вычислении суммы полагаем, что все значения ep и
p=1
qp–1 представлены в десятичной системе счисления.
Максимальное n-разрядное число получается при ep=q–1 для всех p:
n
Emax = q 1 q p 1 = q n 1 .
p=1
Пример: при n = 3 и q = 10 максимальное n-разрядное число 103 – 1 =
999.
Из этого следует, что существует qn различных n-разрядных чисел (с учѐтом нуля).
Пример: при n = 3 и q = 10 количество n-разрядных чисел 103 = 1000.
Перевод числа из системы счисления с произвольным основанием q в десятичную систему счисления (q = 10) выполняется по приведенным формулам, для чего требуется перевести в десятичную систему счисления только числа ep и q.
Пример:
(3F)16 = X10
(3F)16 = 15*161-1 + 3*162-1 = 15 + 48 = 6310
Пример:
(1101)2 = X10
X10 = 1*21-1 + 0*22-1 + 1*23-1 + 1*24-1 = 1 + 4 + 8 = 1310
Двоичная система счисления широко используется в вычислительных устройствах для передачи, преобразования и хранения информации. Преимущество двоичной системы счисления перед системами счисления с другими основаниями – простота реализации устройств передачи и хранения (обычно оперируют отсутствием (0) и наличием (1) напряжения).
Код Грея – система счисления, в которой два соседних значения различаются только в одном разряде. Наиболее часто на практике применяется рефлексивный (отражѐнный) двоичный код Грея
2-битный код Грея
00
01
11
10
3-битный код Грея
000
001
011
010
110
111
101
100
4-битный код Грея
0000
0001
0011
0010
0110
0111
0101
0100
1100
1101
1111
1110
1010
1011
1001
1000
