Заключение

Разработано много методов численного решения краевых задач для обыкновенных дифференциальных уравнений. В ходе данной работы изучались наиболее часто используемые из них - метод конечных разностей и метод прогонки.

Метод конечных разностей был разработан раньше остальных и на первый взгляд является наиболее простым в реализации. Идея его состоит в разбиении прямоугольной сеткой области, в которой решается уравнение, и дискретизация дифференциального оператора. Решая линейную систему уравнений, находят приближенные решения в узлах решетки. Основные трудности связаны с учетом граничных условий, если граница области имеет сложную геометрическую форму. К недостаткам метода следует отнести плохую аппроксимацию границ сложных областей.

Метод прогонки является вариантом метода исключения Гаусса для системы, в каждое уравнение которой входят лишь по три неизвестных значения y в соседних узлах сетки. Этот метод очень выгоден: число операций в нем пропорционально числу уравнений. В то же время для произвольной системы n линейных алгебраических уравнений число операций в обычном методе исключения пропорционально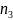 . Кроме этого, метод прогонки имеет очень простой алгоритм вычислений и может быть легко реализован при расчетах на вычислительной технике.

Список использованных источников

1 Демидович, Б. П. Численные методы анализа. Приближение функций, дифференциальные и интегральные уравнения / Б. П. Демидович, И. А. Марон, Э. З. Шувалова.  М. : Наука, 1967.  368 с.

2 Березин, И. С. Методы вычислений / И. С. Березин, Н. П. Жидков.  М. : Физматгиз, 1985.  620 с.

3 Поршнев, С. В. Численные методы на базе Mathcad / С. В. Поршнев, Е. Ю. Беленкова.  СПб. : БХВ-Петербург, 2012.  458 с.

4 РД ФГБОУ ВО «КнАГТУ» 013-2016. Текстовые студенческие рабо- ты. Правила оформления.  Введ. 2016-03-10. – Комсомольск-на-Амуре : ФГБОУ ВО «КнАГТУ», 2016. – 55 с.