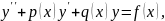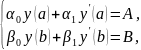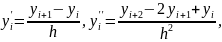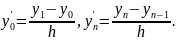Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Комсомольский-на-Амуре государственный
университет»
Факультет компьютерных технологий
Кафедра «Прикладная математика и информатика»
РАСЧЁТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ
по дисциплине «Численные методы»
Решение краевых задач для обыкновенных
дифференциальных уравнений
Студент группы 5МИб-1 Н.С. Самойлов
Преподаватель О.В. Козлова
2017
Содержание
Введение…………………………………………………………………… 3
1 Решение краевой задачи для обыкновенных дифференциальных
уравнений методом конечных разностей ……………………………… 4
2 Решение краевой задачи для обыкновенных дифференциальных
уравнений методом прогонки……………………………………….….. 7
Заключение………………………………………………………………… 11
Список использованных источников...…………………………………... 12
Введение
На практике часто возникает необходимость решения краевых задач для обыкновенных дифференциальных уравнений. Отличие краевой задачи от задачи Коши (задачи с начальными условиями) состоит в том, что решение дифференциального уравнения должно удовлетворять граничным условиям, связывающим значения искомой функции более чем в одной точке.
Точные решения краевых задач для дифференциальных уравнений удаётся получить лишь в частных случаях. Поэтому эти задачи решают в основном приближённо.
Методы приближенного решения краевой задачи разделяются на две группы:
- Разностные методы (позволяют найти приближенное решение в виде таблицы);
- Аналитические методы (позволяют найти приближенное решение в виде аналитического выражения).
Одним из наиболее простых методов решения краевой задачи является сведение ее к системе конечно-разностных уравнений и метод прогонки.
1 Решение краевой задачи для обыкновенных дифференциальных
уравнений методом конечных разностей
Решение краевой задачи для уравнения:
|
|
(1.1) |
|
|
(1.2) |
состоит
в определении значений функции y(x),
удовлетворяющей данному уравнению
(1.1) и краевым условиям (1.2), где p(x),
q(x),
f(x)
- известные непрерывные на отрезке [a,b]
функции,
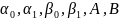 -
заданные постоянные, причем
-
заданные постоянные, причем
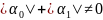 и
и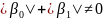 .
Если A=B=0, то краевые условия называются
однородными.
.
Если A=B=0, то краевые условия называются
однородными.
Разобьем
отрезок [a,
b]
на n равноотстоящих узлов с некоторым
шагом
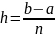 .
Точки разбиения имеют абсциссы
.
Точки разбиения имеют абсциссы
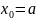 ,
,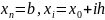 (
(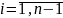 ).
).
Получаемые
в результате расчета приближенные
значения искомой функции y(x)
и ее производных y'(x),
y'(x)
в узлах
 обозначим через
обозначим через
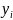 ,
,
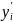 ,
,
 соответственно.
Также введем обозначения
соответственно.
Также введем обозначения
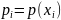 ,
,
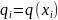 ,
,
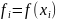 .
.
Заменим приближенно в каждом внутреннем узле производные конечноразностными отношениями:
|
|
(1.3) |
а на концах отрезка положим:
|
|
(1.4) |
Подставив (1.3), (1.4) в уравнение (1.1) и условия (1.2):
|
|
(1.5) |
Получим линейную систему n+1 алгебраических уравнений с n+1 неизвестными. Решив ее, получим таблицу приближенных значений искомой функции
Задание: Используя метод конечных разностей, составить решение краевой задачи для обыкновенного дифференциального уравнения точностью =10-3; шаг h= 0,1.
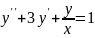
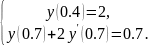
Разбив отрезок [0,4; 0,7] на части с шагом h=0,1 получим четыре узловые точки c абсциссами x0=0,4; x1=0,5; x2=0,6; x3=0,7. Две точки x0=0,4 и x3=0,7 являются конечными, а две другие – внутренними.
Заменим приближенно в каждом внутреннем узле и концах отрезка производные конечно-разностными отношениями (1.3) и (1.4). Составим систему линейных алгебраических уравнений.

Для решения систем в Mathcad имеется специальный вычислительный блок, состоящий из трех частей, идущих последовательно друг за другом:
Given — ключевое слово;
Система, записанная логическими операторами в виде равенств и, возможно, неравенств;
Find(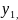 ...
,
...
,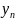 )
— встроенная функция для решения
системы.
)
— встроенная функция для решения
системы.
Решая систему, получим таблицу приближенных значений искомой функции.
Таблица 1 – Метод конечных разностей для решение краевой задачи
|
|
|
0 |
0.4 |
2 |
1 |
0.5 |
1.969 |
2 |
0,6 |
1.92 |
3 |
0,7 |
1.865 |
Реализация метода конечных разностей в Mathcad (рисунок 1).
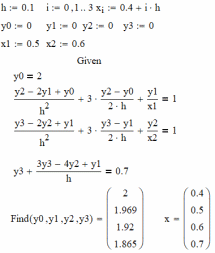
Рисунок 1 – Метод конечных разностей в Mathcad