1.5 Кешіктіру буын
Кешіктіруші деп шығыс шама кіріс шаманың өзгерісін еш бөгетсіз, бірақ кейбір тұрақты τ кешіктірумен жүргізетін буынды айтамыз.
Кешігуші үзбенің анықтамасына Хкір кіріс шамасы мен Хшығ шығыс шама арасындағы тәуелділікті аламыз.
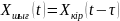
Мұндағы τ- таза кешігу уақыты
Нөлдік баспапқы шарттардағы операторлық түрдегі теңдеуді кешігу теоремасы пайдалана отырып аламыз.
Кешігуші буынның беріліс функциясы:
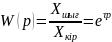
Амплитудалы – фазалы сипаттаманың теңдеуі:
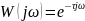
ω-ні 0-ден ∞-ге дейін өзгерткен кезде W(jω) векторы сағат тілі бойынша айналады, ол кезде өзінің ұзындығын өзгертпейді. Осылай, кешігуші үзбенің амплитудалы-фазалық сипаттамасының ортасы координата басында және радиусы бірге тең шеңберді береді.
өрнегінің тригонометриялық түрі:
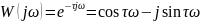
Нақты және жорамал жиіліктік сипаттаманың теңдеуі
P(ω)=cosτω
Q(ω)=-sinτω
ω-ны 0-ден ∞-ке дейін өзгерткен кезде нақты және жорамал жиіліктік сипаттамасы амплитудалық жиіліктік сипаттамасының косинусоидасы мен синусоидасына сәйкес береді.
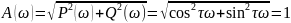
Фазалық жиіліктік сипаттама теңдеуі:
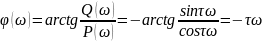
ω-ны 0-ден ∞-ке дейін өзгерткен кезде φ(ω) 0-ден ∞-ке дейін өзгереді.
P(0)=cosτω=cos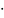
1.9
0=1
Q(0)=-sinτω=-sin
1.9
5-кесте - Кешіктіру буынның нақты және жорамал жиіліктік сипаттамаларының есептелген мәндері
ω, c-1 |
0 |
10 |
20 |
30 |
40 |
50 |
80 |
190 |
200 |
P(ω) |
1 |
0.95 |
0.79 |
0.54 |
0.24 |
0.08 |
0.88 |
1 |
0.94 |
Q(ω) |
0 |
-0.33 |
-0.62 |
-0.84 |
-0.97 |
-0.99 |
-0.47 |
-0.02 |
-0.34 |
|
0 |
-1,9 |
-3,8 |
-5,7 |
-7,6 |
-9,5 |
-11,4 |
-15,2 |
-38 |
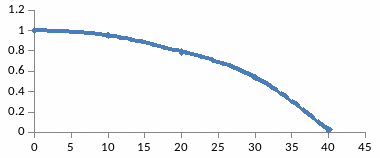
16-Сурет – Кешігу буынның нақты жиіліктік сипаттамасы
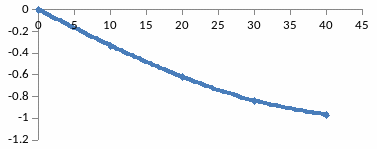
17-Сурет - Кешігу буынның жорамал жиіліктік сипаттамасы
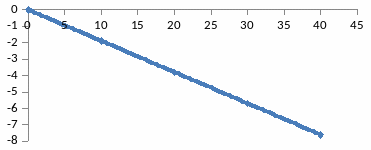
18-Сурет - Кешігу буынның фазалық жиіліктік сипаттамасы
1.6 Тербелмелі буын
Тербелмелі деп екінші ретті буын аталады, оның кірісіне сатылы әсерді алған кезде шығыс шама өшіп – жанатын тербеліс жасай отырып, жаңа орнатылған мәнге ұмтылады. Бұл буынның ерекшелігі Х кіріс санның өзгерген кезде тербелмелі құбылыс арқылы У шығыс санын өзгертеді.
Динамикалық режиміндегі тербелмелі буынның операторлық мағынасы:
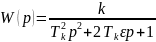
Мұндағы Т1 және Т2 – тұрақты уақыт, периодты сипаттайтын және өздік тербелмелі буынның өшу уақыты
k- буын күшею коэффициенті
Қосалқы
функцияны өзгертеміз
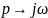
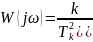
Нақты және жорамал жиіліктік сипаттаманың теңдеулері
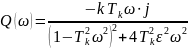
Амплитудалық және фазалық жиіліктік сипаттама теңдеулері
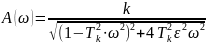
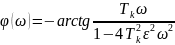
7-кесте - Тербелмелі буынның жиіліктік сипаттамаларының есептелген мәндері
-
ω, c-1
0
2
4
6
8
10
12
14
16
-2.7
-0.08
-0.02
-0.009
-0.005
-0.003
-0.002
-0.0015
-0.0012
0
-0.03
-0.001
-0.003
-0.0002
-0.0001
-0.00006
-0.00004
-0.00003
A(ω)
2.7
0.08
0.02
0.009
0.005
0.003
0.002
0.002
0.001
(ω)
11
7.4
4
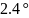
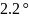
1.7
1.5
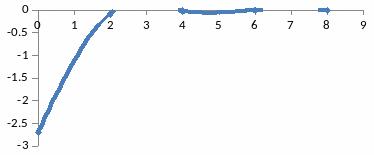
19-Сурет – Тербелмелі буынның нақты жиіліктік сипаттамасы
20-Сурет – Тербелмелі буынның жорамал жиіліктік сипаттамасы
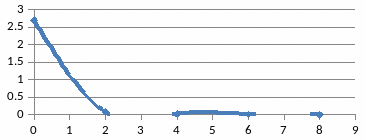
21-Сурет – Тербелмелі буынның амплитудалық жиіліктік сипаттамасы
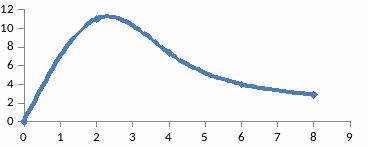
22-Сурет – Тербелмелі буынның фазалық жиіліктік сипаттамасы