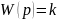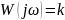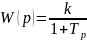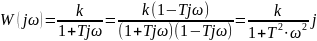КІРІСПЕ

Жиіліктік сипаттамалар (ЖС) автоматты реттеу жүйелерін (АРЖ) анализдеу және синтездеу кезінде кең пайдаланылады. Типтік динамикалық буындардың (ТДБ) және жүйелердің жиіліктік сипаттамаларының өрнектері беріліс функциялардан (БФ) алынуы мүмкін. Ол үшін операторлық түрде жазылған беріліс функцияларында p операторы 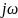ауыстырылады.

Сызықтық ТДБ немесе АРЖ кірісіне гармоникалық әсер берген кезде:

((1)

ауыспалы процесс біткен кезде, шығыс сипаттаманың да түрі периодтық функция болады:

((2)

Бұл функция кіріс функциясынан амплитуда және фаза бойынша ерекшеленеді, бірақ жиіліктері бірдей болады. Осы кезде ТДБ немесе АРЖ еріксіз тербеліс режимінде болады.

((3)

қатынасы ТДБ немесе САРЖТ комплексті күшейту коэффициенті деп аталады. Ол комплексті жиіліктік функциядан көрініс табады.

Осылайша шығыс шамасын комплексті жиілік функциясына кіріс шамасының көбейтіндісі деп алуға болады, яғни:

((4)

W(j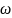 ) өрнегін нақты D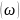 және жорамал Q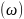 бөліктеріне бөлуге болады:

((5)

Мұндағы: P , Q , A , 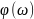– бойынша полиномдар.

Жиілік өзгерген кезде амплитуда A және фаза өзгереді. Олардың соңы комплексті айнымалы жазықтығында қисықты суреттейді. Ол қисық ТДБ немесе тұйық (жабық) АРЖ-ың амплитуда-фазалық жиіліктік сипаттамасы (АФЖС).

Сонымен, жиілік өзгерген кезде P, Q, A, 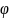шамалары да өзгереді. Сондықтан осы шамалар үшін де жиіліктік сипаттамаларды құруға болады. Осыған сәйкес:

P – нақты жиіліктік сипаттама (НЖС);

Q – жорамал жиіліктік сипаттама (ЖЖС);

А_ж( ) – амплитудалық жиіліктік сипаттама (АЖС);

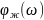– фазалық жиіліктік сипаттама (ЖЖС).

Сипаттамалар арасындағы қатынас төмендегідей өрнектермен анықталады;

((6)

Осындай сипаттамалар тұйық ( жабық ), ашық жүйелер үшін және ТДБ үшін алынуы мүмкін.

Жиіліктік сипаттамалар жүйенің дифференциалды теңдеулерін есептемеуге мүмкіндік береді. ЖС-ның түрі бойынша жүйенің тұрақтылығы, бірқатар сапа көрсеткіштері туралы білуге болады. Сондай-ақ ЖС бойынша, берілген динамикалық көрсеткіштерді алу үшін, жүйені түзету амалдарын (құралдарын) анықтауға болады.

Типтік динамикалық буындардың жиіліктік сипаттамаларын есептеу және құру

Элементтер мен автоматты басқару жүйесі (АБЖ), динамикалық теңестірулермен сипатталуын қарапайым блоктормен көрсетуге болады. Қарапайым блоктардың классификациялық белгілеріне байланысты бірнеше топқа біріккен:

1. Инерциялық буын

2. Инерциясыз буын

3. Интегралдаушы буын

4. Дифференциялдаушы буын

5. Тербелмелі буын

6. Кешігу буын

1 Типтік динамикалық буындардың жиіліктік сипаттамаларын есептеу және құру

1. Инерциясыз буын

Инерциясыз деп, шығыс шамасы кіріс шаманы еш бөгетсіз және кешіктірмей көрсететін буынды айтады. Бұл буын қарапайым буындардың тобына кіреді, кіріс өлшемі шығыс өлшеміне пропорционалды:

.

1(7)

Мұндағы k – беру коэффициент

Инерциясыз буынның беріліс функциясы:

((8)

Берілген беріліс функцияның амплитудалық – жиіліктік сипаттамасын (АЖС), фазалық – жиіліктік сипаттамасын (ФЖС), амплитуда – фазалық жиіліктік сипаттамасын (АФЖС), белгілеп нақты жиіліктік сипаттамасын (НЖС) және жорамал жиіліктік сипаттамасын (ЖЖС) тұрғызу.

Беріліс функциясында Лаплас р операторын jω – ға ауыстырамыз.

((9)

Жорамал және нақты бөліктерін белгілеп аламыз.

P(ω)=k	((10)
Q(ω)=0	((11)

Амплитудалы жиілік сипаттама

((12)

Фазалы жиілік сипаттама

((13)

1- кесте - Инерциясыз буынның жиіліктік сипаттамаларының есептелген мәндері

ω, c-1	0	1	2	3	4	6	8	20	∞
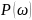
	12.9	12.9	12.9	12.9	12.9	12.9	12.9	12.9	0
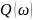
	0	0	0	0	0	0	0	0	0
	12.9	12.9	12.9	12.9	12.9	12.9	12.9	12.9	0

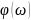
Инерциясыз буынның жиіліктік сипаттамаларының графиктері 1 - 4 – суреттерде көрсетілген.

1–Сурет – Инерциясыз буынның нақты жиіліктік сипаттамасы

2-Сурет – Инерциясыз буынның жорамал жиіліктік сипаттамасы

3-Сурет – Инерциясыз буынның амплитудалық жиіліктік сипаттамасы

4-Сурет – Инерциясыз буынның фазалық жиіліктік сипаттамасы

1.2 Инерциялық буын

Инерциялы деп бірінші ретті буынды айтамыз, кірісіне сатылы әсерді берген кезде шама апериодты түрде жаңа орнатылған мәнге ұмтылады. Бұл буынның шығыс сипаттамасы кіріс сипаттамасына пропооционалды болады.

Инерциялық буынның беріліс функциясы

((14)

Мұндағы k- пропорционалдық коэффициенті

Осы буынның барлық ЖС – ның өрнегін анықтаймыз. Ол үшін беріліс функциясында Лаплас p операторын j – ға ауыстырамыз.

Онда:

((15)

Бұл өрнектен аламыз:

	((16)
	((17)

(6) өрнегін пайдалана отырып, аламыз:

	((18)
	((19)

Жоғарыда алынған өрнектер бойынша ЖС-дың есебін жүргіземіз. Есептің нәтижелерін, өрнектерге алдын ала берілген сандық мәндері қоя отырып: k=9 және T=0.с

=

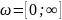
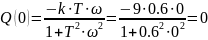
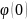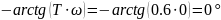
2-кесте - Инерциялы буынның жиіліктік сипаттамаларының есептелген мәндері

ω, c-1	0	1	2	4	5	6	8	20	∞
	9	6.6	3.7	2.1	1.3	0.9	0.4	0.06	0
	0	-4	-4.4	-3.2	-2.7	-2.3	-1.8	0.7	0
	9	7.7	5.8	3.5	2.8	2.4	1.8	0.8	0

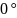
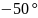
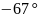
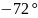
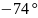
Инерциялы буынның жиіліктік сипаттамаларының графиктері 5 - 10 – суреттерде көрсетілген.

Инерциялы буынның АФЖС-ын P(ω) және Q(ω) мәндері бойынша декарт координатында 5-суретте, А(ω) және φ(ω) мәндері бойынша поляр координатында 6-суретте көрсетілген.

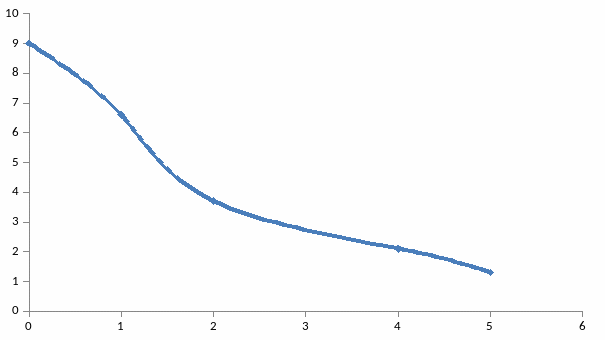
5-Сурет - Инерциялы буынның нақты жиіліктік сипаттамасы

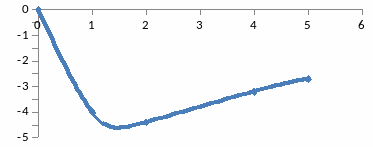
6-Сурет - Инерциялы буынның жорамал жиіліктік сипаттамасы

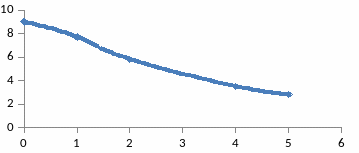
7-Сурет - Инерциялы буынның амплитудалық жиіліктік сипаттамасы

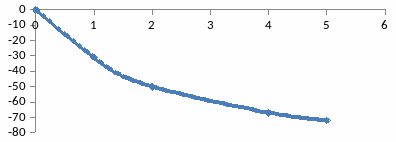
8-Сурет - Инерциялы буынның фазалық жиіліктік сипаттамасы

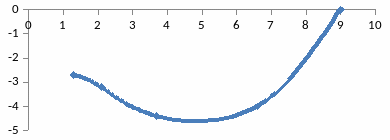
9-Сурет - Инерциялы буынның декарт координатасында салынған ампитудалық - фазалық жиіліктік сипаттамасы
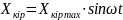
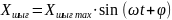
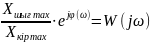
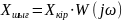
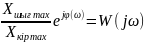
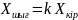