Мазмұны

Кіріспе

1. Алғашқы берілгендері ……………………………………………………….4

2.Негізгі бөлім …………………………………………………………………..5

2.1. Кирхгофтың заңдары бойынша теңдеулер жүйесін құрастырып есептеу …………………………………………………………………………..5

2.2 Контурлық әдіс бойынша есептеу ……………………………………7

2.3 Түйіндік потенциалдық әдіс бойынша есептеу …………………….10

2.4 Потенциалдық диаграмма ……………………………………………13

2.5 Қуаттар балансы ………………………………………………………14

3.Қорытынды ……………………………………………………………………15

Қолданылған әдебиеттер тізімі

Кіріспе

Тұрақты ток – ток күшінің шамасы мен бағыты уақытқа байланысты өзгермейтін электр тогы. Тұрақты ток тұрақты кернеудің әсерімен тек тұйықталған тізбекте ғана пайда болады. Тармақталмаған тұйық тізбектің кез келген қимасында тұрақты ток күшінің мәні өзгермейді. Тұрақты токтың негізгі заңдарына ток күші мен кернеудің байланысын сипаттайтын Ом заңы, өткізгішпен ток жүрген кезде бөлініп шығатын  жылуды анықтайтын  Джоуль-Ленц заңы және тармақталған тізбек үшін жазылатын Киргхоф ережелері жатады. Тұрақты ток көздеріне электр машиналарының генераторы,гальвани элементтері, термоэлементтер, батареяларға топтастырылған фотоэлементтер, күн көзінің батареялары, алдын ала зарядталған аккумуляторлар және —пайдалы әсер коэффициенті жоғары магниттік гидродинамика генераторлары жатады. Тұрақты токты жартылай өткізгіштердің және басқа түзеткіштердің көмегімен,айнымалы токты түзету арқылы өндіруге болады.

Кирхгофтың бірінші заңын екі түрде тұжырымдауға болады:

1) схеманың кез – келген түйініне келетін токтардың алгебралық қосындысы нөлге тең;

2) түйінге келетін токтардың қосындысы, одан кететін токтардың қосындысына тең;

Сонымен, түйіндегі токтардың алгебралық қосындысы нөлге тең; түйінге келетін токтар оң таңбалы, ал одан шығатын токтар теріс таңбалы болады.

Физикалық тұрғыдан алып қарағанда, Кирхгофтың бірінші заңы бойынша, тізбектегі зарядтардың қозғалысы кезінде, түйіндердің ешқайсысында да зарядтар жинақталмайтындығы байқалады.

Кирхгофтың екінші заңын да екі түрлі жолмен тұжырымдауға болады:

1) кез – келген тұйық контурдағы кернеудің түсуінің алгебралық қосындысы осы контур бойындағы барлық ЭҚК-нің алгебралық қосындысына тең болады;

2) кез – келген тұйық контурдың бойындағы кернеулердің (бұл жерде кернеудің түсуі емес) алгебралық қосындысы нөлге тең;

Есептің берілгені:

R₁=13 Oм; R₂=5 Ом; R₃=9 Ом; R'₄=12 Ом; R''₄=16,8 Ом; R₅=10 Ом;

R' ₆=0 Ом; R''₆=4 Ом; E₂=10 B; E₃=21 B; I_k2=0 A; I_k3=1 A;

Берілген сұлбаны түрлендіреміз:

Алдымен ЭҚК түрлендіреміз:

E'₂= I_k2· R₂=0·2=0 B

E''₂= E₂ + E'₂= 10+0= 10 B

E'₃= R₃· I_k3= 9·1= 9 B

E''₃= E'₃+ E₃= 9+21= 30 B

Келесіде кедергілерді R орналасуына байланысты есептеп түрлендіреміз:Егер бірнеше резисторлар бірінен соң бірі тармақтарсыз қосылған болса және олардан бір тоқ өтсе, ол тізбектелген деп аталады. Тізбектей жалғанған кедергілерді R' ₆ , R''₆ белгілейміз және есептейміз:

R'''₆= R' ₆+ R''₆= 0+4= 4 Oм

Келесіде R'₄ , R''₄ кедергілерін параллель қосамыз:R'''₄= = = 7 Ом

Кирхгофтың заңдары бойынша теңдеулер жүйесін құрастыру

Электр тізбегінің контурлары мен түйіндеріне арнап Кирхгофтың бірінші және екінші заңдарымен теңдеулер құрастыру, тармақтардағы белгісіз токтарды және олар арқылы элементтердегі кернеуді анықтау. Сондықтан, белгісіздер саны, тармақтар санына -b- тең, демек Кирхгофтың бірінші және екінші заңдарымен осыншама белгісіз теңдеулер құрастыру керек.

Теңдеулер саны, бірінші заң арқылы құрайтын тізбектің түйін саны y болса, тең деп (y-1) болады, теңдеулер бір-біріне байланысты емес. Теңдеулер тәуелсіздігі мынада, түйінді таңдағанда тәртіп енгізуге болады, ал келесі түйін бұрынғыдан бір тармақпен өзгеше. Қалған теңдеулер Кирхгофтың екінші заңымен тәуелсіз контурлардан құралады, яғни теңдеулер саны:

b - (y-1)= b – y + 1 (1.1)

Егер басқа контурларға кірмейтін бір тармақ болса, онда контур тәуелсіз деп аталады, электр тізбегіне Кирхгофтың теңдеулер жүйесін құрастырамыз. Схемада төрт түйін мен алты тармақ бар. Сондықтан Кирхгофтың бірінші теңдеу бойынша үш теңдеу, ал екіншісіне үш теңдеу құрастырамыз.

Кирхгофтың бірінші заңына теңдеу:

I₂ – I₅ – I₃ = 0

I₅ – I₁ + I₆ = 0

I₃ – I₆ – I₄ = 0

Кирхгофтың екінші заңына теңдеу:

I₅R₅ + I₁R₁ + I₂R₂ = E''₂

I₃R₃ + I₆R₆ – I₅R₅ = E''₃

I₄R₄ – I₁R₁ – I₆R₆ = 0

Контурлық әдіс бойынша есептеу.

Контурлық токтар әдісінде,схеманың әрбір тәуелсіз контурында, өзінің контурлық тогы жүруге тиіс деп есептейді. Контурлық токтарға салыстырып, теңдеулер құрады да, сонан кейін контурлық контур арқылы тармақтардағы токтар анықталады.

Әр контурға өзінің контурлық мәндерін белгілейміз:

I₁₁, I₂₂, I₃₃

Біздің тізбегімізде контурлық тоқтар сағат тіліне бағыттас

Теңдеулер жүйесін құрамыз:

I₁₁R₁₁ + I₂₂R₁₂ + I₃₃R₁₃ = E₁₁

I₁₁R₂₁ + I₂₂R₂₂ + I₃₃R₂₃ = E₂₂

I₁₁R₃₁ + I₂₂R₃₂ + I₃₃R₃₃ = E₃₃

Мұндағы:

R₁₁ = R₅ + R₂ + R₁ = 10+5+13 = 28 Ом

R₂₂ = R₃ + R'''₆ + R₅ = 9+4+10 = 23 Ом

R₃₃ = R'''₄ + R₁ + R'''₆ = 7+13+4 = 24 Ом

R₁₂ = R₂₁ = - R₅ = -10 E₁₁ = E''₂ = 10

R₁₃ = R₃₁ = - R₁ = -13 E₂₂ = E''₃ = 30

R₂₃ = R₃₂ = - R'''₆ = -4 E₃₃ = 0

R₁₁ R₂₂ R₃₃ - бірінші,екінші,үшінші контурлардың толық немесе жекеше кедергілері.

R₁₂ R₁₃ R₂₃ – бірінші мен екінші,бірінші мен үшінші,екінші мен үшінші контурлар арасындағы кедергілер алу белгілері.

E₁₁ E₂₂ E₃₃ – бірінші,екінші,үшінші контурлардың контурлы ЭҚК-сы(ЭҚК бағыты, контурды аралау бағытымен сәйкес болса, ЭҚК белгісі плюс болады).

Егер де ЭҚК бағыты контурдың бағытымен бағыттас болса, онда «+», қарама – қарсы болса «-» таңбасы алынады.

Берілген теңдеуді матрица арқылы шыгарамыз. Крамер әдісімен шыгарған ыңғайлы болып тұрғандықтан осы әдіспен шығарамыз.

Енді орнына сандарды қоямыз.Алдымен анықтауышын есептеп аламыз:

R₁₁ R₁₂ R₁₃ 28 -10 -13

Δ = R₂₁ R₂₂ R₂₃ = -10 23 -4 = 7681

R₃₁ R₃₂ R₃₃ -13 -4 24

Анықтауыш арқылы I₁₁ тогын анықтауға болады. Ол үшін формулага койып есептейміз. Анықтауыштың бірінші қатарына ЭҚК алмастырып , I₁₁ үшін анықтауыш есептейміз.

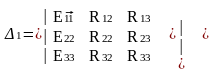
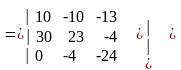= 14120

Шыққан цифраны формулаға қойамыз

I₁₁ =

Дәл осы әдіс арқылы I₂₂ контуры үшін есептейміз, және бұл жолы ЭҚК мәндерін екінші қатарға орналастырамыз.

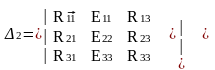
28 10 -13

Δ₂= -10 30 -4 = 18010

-13 0 -24

I₂₂=

Келесіде I₃₃ контуры үшін есептейміз, енді бұл жолы ЭҚК үшінші қатарға орналастырып шығарамыз.

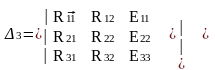
28 -10 10

Δ₃ = -10 23 30 = 10650

-13 -4 0

I₃₃ =

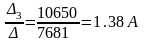
Бұл матрицаны компьютердің көмегімен Mathcad Professional программасы арқылы есептелінеді немесе қолмен есептеуге болады.

Енді әрбір тармақтағы тоқты анықтаймыз:

I₁=I₁₁ – I₃₃ = 0.45 A I₄=I₃₃=1.38 A

I₂=I₁₁= 1.83 A I₅=I₁₁ – I₂₂= -0.51 A

I₃=I₂₂= 1.38 A I₆=I₂₂ – I₃₃ = 0.96 A

Енді Кирхгофтың бірінші заңы бойынша тексереміз.

2-ші түйін : I₂-I₅-I₃=1.83+0.51-2.34=0 0=0

3-ші түйін : I₃-I₆-I₄= 2.34-0.96-1.38=0 0=0

1-ші түйін : I₅-I₁+I₆= -0.51-0.45+0.96=0 0=0