6. Собственные функции и собственные значения. Стационарное уравнение Шредингера.

Уравнение называется уравнением Шредингера для стационарных состояний. В это уравнение в качестве параметра входит полная энергия Ечастицы. В теории дифференциальных уравнений доказывается, что подобные уравнения имеют бесчисленное множество решений, из которых посредством наложения граничных условий отбирают решения, имеющие физический смысл. Для уравнения Шредингера такими условиями являются условия регулярности волновых функций: волновые функции должны быть конечными, однозначными и непрерывными вместе со своими первыми производными. Таким образом, реальный физический смысл имеют только такие решения, которые выражаются регулярными функциями y. Но регулярные решения имеют место не при любых значениях параметра Е, а лишь при определенном их наборе, характерном для данной задачи. Эти значения энергии называются собственными. Решения же, которые соответствуют собственным значениям энергии, называются собственными функциями. Собственные значения Е могут образовывать как непрерывный, так и дискретный ряд. В первом случае говорят о непрерывном, или сплошном, спектре, во втором — о дискретном спектре.

7. Квантомеханическое представление свободно движущейся частицы.

При движении свободной частицы (U(x) = 0) ее полная энергия совпадает с кинетической. Для свободной частицы, движущейся вдоль оси х, уравнение Шредингера для стационарных состояний примет вид .Прямой подстановкой можно убедиться в том, что частным решением уравнения i является функция , где A=const иk = const, с собственным значением энергии Функция представляет собой только координатную часть волновой функции Поэтому зависящая от времени волновая функция, согласно , (219.3) (здесь Функция представляет собой плоскую монохроматическую волну де Бройля). Из выражения следует, что зависимость энергии от импульса оказывается обычной для нерелятивистских частиц. Следовательно, энергия свободной частицы может принимать любые значения (так как волновое числоk может принимать любые положительные значения), т. е. ее энергетический спектр является непрерывным. Таким образом, свободная квантовая частица описывается плоской монохроматической волной де Бройля. Этому соответствует не зависящая от времени плотность вероятности обнаружения частицы в данной точке пространства.

8. Квантомеханическое описание частицы в бесконечно глубокой прямоугольной потенциальной яме.

Проведем качественный анализ решений уравнения Шредингера применительно к частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси х) где l — ширина «ямы», а энергия отсчитывается от ее дна.

Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде

. На границах «ямы» (при х = 0 и х = l) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид

Общее решение дифференциального уравнения : Так как . Тогда Условие выполняется только при гдеп — целые числа, т. е. необходимо, чтобы . Cледует, что т. е. стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях , 'зависящих от целого числа п. Следовательно, энергия £„ частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т. е. квантуется. Квантованные значения энергии называются уровнями энергии, а число п, определяющее энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне £„, или, как говорят, частица находится в квантовом состоянии п.

Тепловое излучение. Абсолютно чёрное тело

Излучение тела, обусловленное тепловым движением молекул, называется тепловым, так как происходит за счёт энергии теплового движения молекул (атомов). Любое тело с температурой Т≠0, излучает, причём спектр излучения – сплошной. Тепловое излучение – единственное излучение, способное находиться в термодинамическом равновесии с веществом. Если уменьшение энергии тела при излучении восполняется за счёт поглощения излучения, падающего на тело из окружающей среды, то излучение называется равновесным.

Тепловое излучение тел может быть охарактеризовано следующими величинами:

1) Интегральная интенсивность излучения численно равна энергии всех длин волн, излучаемой за единицу времени с единичной площади поверхности тела:

. (20.1)

Эту величину называют также полной энергетической светимостью. Она зависит от абсолютной температуры тела. Размерность :

.

2) Монохроматическая (дифференциальная) интенсивность излучения (спектральная плотность энергетической светимости) численно равна энергии, излучаемой за единицу времени с единичной площади поверхности тела в единичном интервале длин волн:

(20.2)

или частот:

. (20.2а)

Размерности:

; .

Монохроматическая интенсивность излучения является функцией длины волны и температуры (20.2) или частоты и температуры (20.2а). Найдём связь между и . Из (20.2) и (20.2а):

. (20.3)

Связь между интегральной и монохроматической интенсивностями излучения:

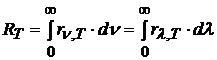(20.4)

Это значит, что площадь под графиком зависимости или равна .

Из всей падающей на тело энергии dWпадающ. монохроматического света в интервале длин волн [l; l+dl] часть энергии dWпоглощ. поглощается телом.

3) Спектральная поглощательная способность тела – это величина, показывающая, какую долю энергии падающего излучения в интервале длин волн [l; l+dl] вблизи данной длины волны l тело поглощает:

, (20.5)

.

Тело называется абсолютно чёрным (АЧТ), если поглощает всё излучение, падающее на него. Для абсолютно черного тела

.

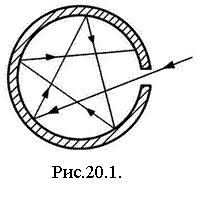
В природе не существует абсолютно чёрных тел. Тела, покрытые сажей или платиновой чернью, приближаются по своим свойствам к абсолютно черным лишь в ограниченном интервале длин волн. Наиболее совершенной моделью черного тела может служить небольшое отверстие в непрозрачной стенке замкнутой полости (рис.20.1). Луч света, попадающий внутрь через отверстие, претерпевает многократные отражения от стенок полости, прежде чем он выйдет обратно. При каждом отражении происходит частичное поглощение энергии света стенками. Поэтому независимо от материала стенок интенсивность света, выходящего из полости через отверстие, во много раз меньше интенсивности падающего извне первичного излучения. Эта модель тем ближе по характеристикам к чёрному телу, чем больше отношение площади поверхности полости к площади отверстия.