7. Фотоны: энергия, импульс

Таким образом, свет:

а) излучается дискретными порциями – квантами, фотонами (к этому привело объяснение законов теплового излучения);

б) поглощается тоже квантами (фотоэффект).

Энергия фотона равна

, (20.26)

. (20.26а)

Фотоны – безмассовые частицы:

.

Теория относительности даёт такую связь между полной энергией и импульсом частицы:

.

Отсюда для фотона:

;

;

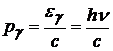; (20.27)

. (20.27а)

8. Давление света

П оскольку фотоны обладают импульсом, то при падении света на поверхность она получает импульс, то есть на поверхность действует сила давления. Впервые измерил давление света около 1900 г. русский физик . Чтобы исключить влияние потоков воздуха на движение лёгких крылышек, в сосуде создаётся вакуум (рис.20.10). Световое давление рассчитывалось по углу закручивания кварцевой нити очень чувствительных крутильных весов, к которым были подвешены крылышки. Количественный результат, полученный в опытах Лебедева, совпал с точностью до 2% с предсказанным теорией Максвелла для электромагнитного поля.

Выражение для светового давления здесь будет получено, исходя из квантовых представлений.

П усть на поверхность с коэффициентом отражения ρ нормально падает свет (рис.20.11). За промежуток времени Δt на площадку S попадает N фотонов. Из них отражается число фотонов, равное N1=ρN, и поглощается N2=(1–ρ)N фотонов. Импульс одного фотона равен

.

При отражении изменение импульса фотона

направлено по нормали к площадке и равно по величине

(см. рис.20.11; здесь – импульс падающего фотона, – отражённого).

Изменение импульса поглощённого фотона равно величине самого импульса:

.

По закону сохранения импульса суммарное изменение импульса фотонов равно величине импульса, полученного площадкой:

,

или

,

откуда по второму закону Ньютона в импульсной форме найдём силу давления света:

,

а затем – давление:

,

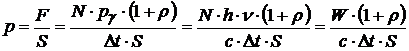где – суммарная энергия всех фотонов, падающих на площадку S за время Δt, то есть находящихся в объёме , на расстоянии от площадки не более, чем . Величина – объёмная плотность энергии, то есть энергия фотонов в расчёте на единичный объём, и тогда

. (20.28)

С другой стороны, давление можно выразить через интенсивность света I. По определению, интенсивностью света называется энергия световой волны, переносимая за единицу времени через единичную площадку, перпендикулярную лучу:

.

Тогда

.

Есть ещё одно понятие, аналогичное интенсивности света: энергетическая освещённость – это энергия света, попадающая на единичную площадку за единицу времени:

,

тогда давление

. (20.29)

Если свет падает на поверхность под углом , то нормальное давление равно

.

(Доказательство см. в третьей части пособия для самостоятельной работы, примеры решения задач; задача № 5.)

9. Эффект Комптона

Комптоновское рассеяние открыто в 1923 году. Комптоновское рассеяние – это упругое рассеяние рентгеновского излучения на свободных электронах. В рассеянных лучах наряду с первичным излучением с длиной волны присутствует излучение с длиной волны (рис.20.12, 20.13), причём изменение длины волны зависит только от угла рассеяния :

. (20.30)

Здесь – комптоновская длина волны.

С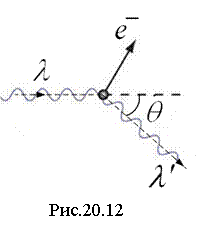 точки зрения классической электродинамики объяснение рассеяния с изменением частоты (длины волны) невозможно. Следуя волновым представлениям, получим, что механизм рассеяния состоит "в раскачивании" электронов электромагнитным полем падающей волны. Колеблющийся электрон должен в свою очередь излучать электромагнитную волну, имеющую частоту, равную частоте колебаний электрона, т. е. частоте падающей волны. Таким образом, свободные электроны рассеивают излучение, причем частота рассеянных волн должна равняться частоте падающих.

Теоретическую интерпретацию явлению дали А. Комптон и П. Дебай. Эффект становится объяснимым, если полагать, что электромагнитное излучение представляет поток фотонов, каждый из которых обладает энергией и импульсом . В «легких» веществах, с которыми проводил опыты А. Комптон (графит, парафин), энергия связи электронов мала по сравнению с энергией, передаваемой ему квантами рентгеновского излучения, и электроны можно считать свободными. При комптоновском рассеянии происходит упругое столкновение фотона со свободным электроном. По образному выражению М. Борна, эффект Комптона – это игра в биллиард фотонами и электронами. Объяснение комптоновского рассеяния явилось одним из главных аргументов в пользу корпускулярной природы электромагнитного излучения.

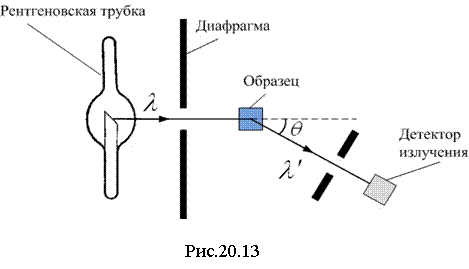
Фотон рассеивается на внешних электронах в атоме, которые можно считать свободными, так как энергия их связи с ядром много меньше энергии фотона. Электрон можно считать покоящимся по той же причине: его кинетическая энергия много меньше энергии фотона. Выполняются законы сохранения импульса и энергии (рис.20.14):

, (20.31)

. (20.32)

Здесь – импульс первичного фотона;

– энергия первичного фотона;

– импульс рассеянного фотона;

– энергия рассеянного фотона;

– энергия покоя электрона;

– энергия электрона отдачи.

Из рис.20.14 по теореме косинусов:

. (20.33)

Взаимосвязь импульса и энергии электрона даёт теория относительности:

,

или

. (20.34)

Из (20.32):

,

тогда

.

Подставим последнее равенство в (20.34):

.

Сокращаем на :

.

Сравниваем с (20.33):

.

Отсюда

.

Сокращаем на :

.

Сокращая на 2, подставляем выражения для импульсов фотонов через длину волны и выражение для энергии покоя электрона:

.

Приводим к общему знаменателю и сокращаем на h:

.

Сокращаем на :

.

Теперь можно выразить :

,

.

Наконец,

,

где и есть комптоновская длина волны.

Тепловое излучение

1.1. Закон Кирхгофа Тепловое излучение – это испускание электромагнитных волн за счёт внутренней энергии тел. Тепловое излучение имеет место при любой температуре. При низких температурах оно сдвинуто в длинноволновую часть спектра. Излучение будет равновесным, если распределение энергии между телом и излучением не меняется для каждой длины волны. Способность теплового излучения быть в равновесии вызвана тем, что интенсивность этого излучения возрастает с температурой. Энергетическая светимость тела R - поток энергии, испускаемый единицей поверхности излучающего тела по всем направлениям (в пределах телесного угла 2?) . Энергетическая светимость – функция температуры. Излучение включает в себя волны различных частот ? (длин волн ?). Пусть

• поток энергии, испускаемый единицей поверхности тела в интервале частот d?, равен .

• Значение мало поэтому

, (1.1) величина называется испускательной способностью тела -это мощность излучения с единицы площади поверхности тела в интервале частот единичной ширины. Испускательная способность есть функция частоты излучения и температуры. Энергетическая светимостъ тела связана с его испускательной способностью формулой . Излучение можно характеризовать вместо частоты длиной волны . Участку спектра соответствует интервал длин волн , причем , тогда, дифференцируя, получаем . Знак минус в этом выражении не имеет существенного значения, он лишь показывает, что с ростом длина волны убывает. Поэтому минус в дальнейшем писать не будем. Доля энергетической светимости, приходящаяся на интервал равна . Так как интервалы и относятся к одному и тому же участку спектра, величины и должны совпадать, т.е. , или , и . (1.2) с помощью формулы (1.2) можно перейти от к и наоборот. Все тела в той или иной степени поглощают энергию падающих на них электромагнитных волн. Спектральной характеристикой поглощения является поглощательная способность тела (коэффициент монохроматического поглощения) , dФ_? - падающий на тело поток электромагнитной энергии, dФ'_?- часть потока, которую поглотило тело, есть функция частоты излучения и его температуры ( 1). Абсолютно чёрное тело - тело полностью поглощающее падающую на него энергию ( = 1). Серое тело - тело, поглощательная способность которого не зависит от частоты и при фиксированной температуре имеет постоянное и меньшее единицы значение, т.е. = , =const<1. При равновесном излучении выполняется правило Прево: если два тела поглощают разные количества энергии, то и излучения у них тоже будут различны. Чем больше испускательная способность тела , тем больше его поглощательная способность а_?T. Закон Кирхгофа утверждает, что отношение испускательной и поглощательной способностей не зависит от природы тела, оно является для всех тел одной и той же (универсальной) функцией частоты (длины волны) и температуры: – универсальная функция Кирхгофа. Для абсолютно чёрного тела =1, поэтому = , таким образом, есть испускательная способность абсолютно чёрного тела. Для характеристики спектрального состава равновесного теплового излучения удобнее пользоваться

• При теоретических исследованиях - функцией частоты .

• В экспериментальных работах предпочтительнее пользоваться функцией , при этом

Тогда и . Абсолютно чёрных тел в природе не существует. Некоторые тела при определённых условиях близки к чёрному:

• Излучение Солнца можно считать близким к излучению абсолютно чёрного тела.

• Чёрная бумага поглощает 96% падающей на неё энергии,

• сажа - 98%, чёрный бархат – 99,6%. Сажа, платиновая чернь имеют , близкую к 1 лишь в ограниченном интервале частот.

• В инфракрасной области <<1.

Однако можно создать устройство, имеющее = 1. Это почти замкнутая полость, имеющая малое отверстие (рис.1.1). Излучение проникает внутрь через отверстие, претерпевая многократные отражения. При каждом отражении часть энергии поглощается. Таким образом, всё излучение полностью поглощается, и из полости выходит излучение, соответствующее по спектральному составу излучению абсолютно чёрного тела при определённой температуре. По этому излучению можно найти экспериментально вид функции f(?,T) или ? (?,T) (рис. 1.2). Дл я каждой кривой имеет место максимум. Это свидетельствует о том, что энергия распределена по спектру абсолютно чёрного тела неравномерно – в области очень малых и очень больших частот абсолютно чёрное тело почти не излучает энергию. С ростом температуры максимум сдвигается в область меньших длин волн. Площадь, ограниченная кривой , пропорциональна энергетической светимости R_?T при данной температуре и растет с ростом температуры. Рассмотрим излучение, находящееся в равновесии с веществом. Для этого представим себе изолированную полость, стенки которой поддерживаются при постоянной температуре Т. В равновесном состоянии энергия излучения будет распределена в объеме полости с определенной плотностью . Спектральное распределение этой энергии можно охарактеризовать функцией , определяемой условием , где - доля плотности энергии, приходящаяся на интервал частот . Полная плотность энергии равна Равновесная плотность энергии излучения зависит только от температуры и не зависит от свойств полости. Найдем связь равновесной плотности энергии излучения с энергетической светимостью абсолютно черного тела . Рассмотрим эвакуированную полость с абсолютно черными стенками. В случае равновесия через каждую точку внутри полости будет проходить в любом направлении поток излучения одинаковой плотности. Ес ли бы излучение распространялось в одном заданном направлении (т.е. через данную точку проходил только один луч), плотность потока энергии в рассматриваемой точке была бы равна произведению плотности энергии и на скорость электромагнитной волны с. Однако через каждую трубку (рис.1.3) проходит множество лучей, направления которых равномерно распределены в пределах телесного угла 4 . Поток энергии также распределен равномерно в пределах этого телесного угла. Следовательно, в каждой точке в пределах телесного угла будет течь поток энергии, плотность которого . Возьмем на поверхности полости элементарную площадку . Эта площадка посылает в пределах телесного угла в направлении, образующем с нормалью угол , поток энергии . По всем направлениям в пределах телесного угла 2 , площадка посылает поток энергии Однако , тогда . Это равенство должно выполняться для каждой спектральной составляющей излучения. Тогда 1.2.Законы теплового излучения абсолютно чёрного тела а) Законы Стефана-Больцмана и Вина. Теоретическое обоснование законов излучения абсолютно черного тела имело огромное значение в истории физики – оно привело к понятию квантов энергии. Для полной характеристики теплового излучения необходимо, как показывает закон Кирхгофа, знать вид функции Кирхгофа f(?,T) , т.е. необходимо установить вид зависимости испускательной способности абсолютно чёрного тела от его температуры.

• В 1879 г. Стефан на основе обобщения экспериментальных данных получил, что энергетическая светимость R любого тела пропорциональна четвёртой степени температуры.

• В 1884 г. учёный Л. Больцман применил к исследованию “чёрного излучения” термодинамический метод и показал, что закон, открытый Стефаном, применим лишь для абсолютно чёрного тела

. Это соотношение получило название закона Стефана-Больцмана. Здесь ? – постоянная Стефана-Больцмана (? = 5,7 . 10 Вт/м К ). Закон Стефана-Больцмана даёт зависимость энергетической светимости от температуры.

• Вин (1893г.) воспользовался, кроме термодинамики, электромагнитной теорией и показал, что функция спектрального распределения должна иметь вид

где F- некоторая функция отношения частоты к температуре. Для функции получается выражение , (1.3) где - некоторая функция произведения . Соотношение (1.3) позволяет установить зависимость между длиной волны , на которую приходится максимум функции , и температурой. Продифференцируем это выражение по : (1.4) Выражение в квадратных скобках представляет собой некоторую функцию . При длине волны , соответствующей максимуму функции , выражение (1.4) должно обращаться в ноль, и, т.к. , то =0. Решение этого уравнения приводит к соотношению: - закона смещения Вина Здесь - постоянная Вина. Длина волны, соответствующая максимальному значению испускательной способности r_?T абсолютно чёрного тела, обратно пропорциональна его температуре. Из этого закона видно, что при понижении температуры абсолютно чёрного тела максимум энергии его излучения смещается в область длинных волн. Поэтому при понижении температуры белое каление переходит в красное, а затем в инфракрасное. б) Исследования Рэлея и Джинса. Физики Рэлей и Джинс представили абсолютно чёрное излучение в замкнутой полости как систему бесконечно большого числа не взаимодействующих друг с другом гармонических осциллятора (радиационных осцилляторов). Собственные частоты ? колебаний радиационных осцилляторов равны частотам соответствующих монохроматических компонент чёрного излучения. Рэлей и Джинс в своих исследованиях

• исходили из теоремы классической статистики о равнораспределении энергии по степеням свободы.

• считали, что на каждое электромагнитное колебание радиационного осциллятора приходится энергия, равная двум половинкам kТ – одна - на электрическую, другая - на магнитную, и получили следующий вид функции Кирхгофа:

. Это выражение называется формулой Рэлея-Джинса. Она хорошо согласуется с экспериментом в области малых частот излучения. В области же больших частот формула приводит к резкому расхождению с экспериментом, с законами Стефана-Больцмана и Вина. Из формулы Рэлея-Джинса следует монотонное возрастание функции f(?,T) с ростом частоты, а на самом деле f(?,T) имеет максимум и далее убывает (рис.1.4). Фо рмула Рэлея-Джинса в области больших частот находится в противоречии с законом сохранения энергии (энергия излучения неограниченно растёт с ростом температуры). Этот результат был назван ультрафиолетовой катастрофой. в) Формула Планка. С классической точки зрения вывод формулы Рэлея и Джинса является безупречным. Поэтому расхождение ее с опытом указывало на существование каких-то закономерностей, несовместимых с представлениями классической физики. В 1900 г. Макс Планк:

• предположил, что гипотеза о непрерывном изменении энергии системы, господствовавшая в классической физике, неприменима к радиационным осцилляторам, а следовательно, к молекулам и атомам излучающего тела, обменивающегося энергией с этими осцилляторами.

• энергия осцилляторов может принимать лишь определённые дискретные значения, равные целому числу элементарных порций энергии

– квантов энергии. Энергия кванта пропорциональна частоте излучения, Таким образом, излучение и поглощение энергии телом происходит не непрерывно, а дискретно, квантами. ћ – постоянная Планка:

• ћ = 1,054 · 10 Дж·с,

• имеет размерность «энергия · время».

• в механике называется действием, поэтому ћ иногда называют квантом действия.

В состоянии равновесия распределение колебаний по значениям энергии должно подчиняться закону Больцмана. Вероятность того, что энергия колебания частоты имеет значение , равна 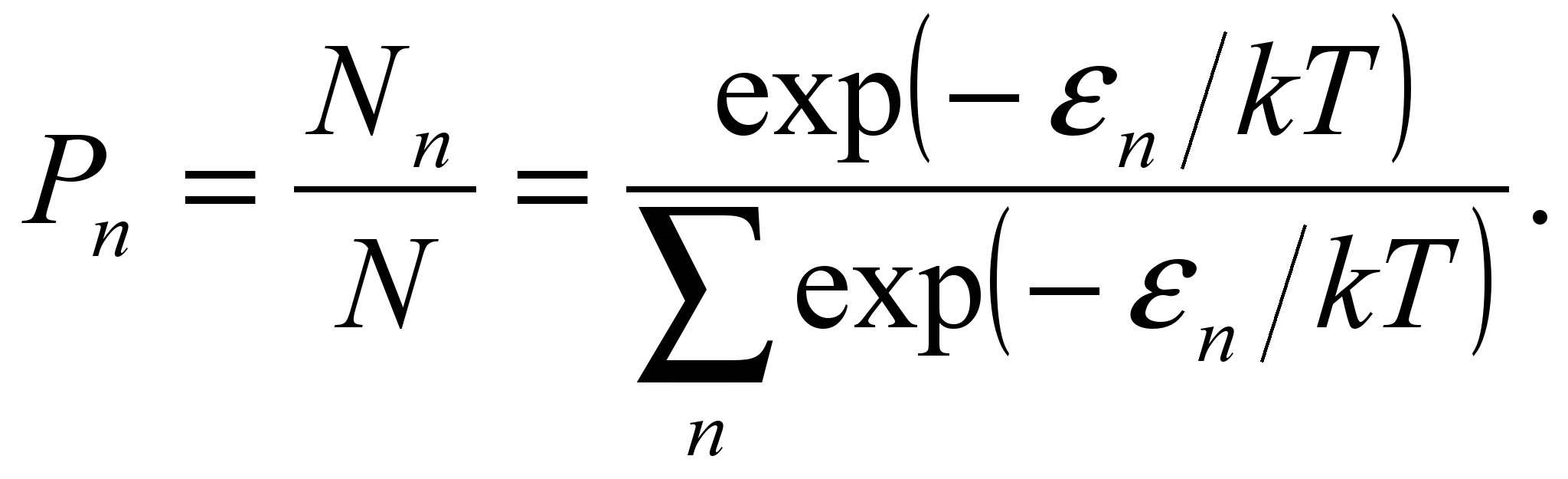Среднее значение энергии колебаний Чтобы произвести вычисления, обозначим и будем считать, что х может принимать непрерывный ряд значений. Тогда (1.5) Под знаком логарифма в этой формуле стоит сумма членов бесконечной геометрической прогрессии с первым членом, равным . Так как знаменатель меньше единицы, прогрессия убывающая, и Подставив эту сумму в (5), получаем При получаем классическое выражение Таким образом, если бы энергия могла принимать непрерывный ряд значений, ее среднее значение было бы равно Плотность энергии, приходящаяся на частотный интервал тогда и . (1.6) Это формула Планка: точно согласуется с экспериментом в интервале частот от 0 до и удовлетворяет критерию Вина . При малых частотах <<1, поэтому можно считать, что , тогда - формула Планка переходит в формулу Рэлея–Джинса. Таким образом, формула Рэлея-Джинса является частным случаем формулы Планка для малых частот. Интегрируя выражение (1.6)и решая уравнение относительно переменной x = , можно получить закон смещения Вина. Таким образом, формула Планка даёт полное описание равновесного теплового излучения. 2. Квантовая механика Физические явления и законы, их описывающие, принято разделять на классические и современные.

• Современная физика опирается на представления о волновой природе вещества, которые возникли в конце 20-х гг.

• Все остальное – классическая физика.

Такие явления как дифракция, интерференция объясняются только волновой теорией. Однако далее будет показано, что и всем частицам (телам) в разной степени присущи волновые свойства, которые значительно влияют на их поведение. Вытекающие из представлений о волновой природе вещества основные положения, составляют предмет квантовой механики. Совершим небольшой экскурс в развитие классической физики. Классическая физика основывалась на законах Ньютона. Она успешно объясняла падение тел, полет снарядов, движение искусственных спутников Земли и другие случаи макроскопического движения (движение тел с малыми скоростями и большими постоянными массами). Механика Ньютона дала нам законы сохранения импульса, момента импульса и энергии. Законы Ньютона и атомно-молекулярные представления о строении вещества легли в основу кинетической теории тепла. Используя понятия заряда и основные законы теории электричества, Максвелл дал объяснение многообразным электрическим и магнитным явлениям, создал в 1870 г. теорию света – самое значительное достижение классической физики. Рассмотрение движения тел со скоростями, близкими к скорости света, трудности в теории эфира при объяснении результатов опыта Морли-Майкельсона, послужили поводом к созданию в 1905 г. Эйнштейном специальной теории относительности, столь противоречащей здравому смыслу. Мы увидим, что волновая природа вещества, корпускулярно - волновой дуализм и их следствия еще более противоречат здравому смыслу. Волновая природа вещества качественно проявляется в том, что каждой частице присущи свойства волны, и наоборот, каждая волна имеет свойства, характерные для частиц. Ярким примером такого дуализма является фотоэффект. 2.1 Фотоэффект Испускание электронов веществом под действием света называется фотоэффектом. Внешний фотоэффект (или фотоэлектронная эмиссия). - если испускание электронов происходит с поверхности твердых тел или жидкости. Внутренний фотоэффект – это перераспределение электронов по энергетическим уровням под действием света. Фотоэффект в газах состоит в ионизации атомов и молекул под действием света и называется фотоионизацией. Электроны, вылетевшие из вещества при внешнем фотоэффекте, называются фотоэлектронами, а электрический ток, который возникает при упорядоченном движении фотоэлектронов, называется фототоком.

• Явление фотоэффекта было впервые обнаружено Герцем в 1887 г. Изучая искровой электрический разряд, он заметил, что ультрафиолетовое излучение в области искрового промежутка облегчает разряд.

• В 1888 г. Гальвакс установил, что причиной этого является появление при облучении свободных зарядов.

• Подробное изучение фотоэффекта провел Столетов. Освещая дугой металлическую пластину, он установил, что при этом пластина теряет заряд только в тех случаях, когда она предварительно была заряжена отрицательно.

Сх ема опытов Столетова имеет вид, представленный на рис.1 Медная сетка С и цинковая пластина Д служат обкладками плоского конденсатора. Этот конденсатор включен через гальванометр в сеть батареи Б. При освещении отрицательно заряженной пластины Д светом от источника S в цепи возникает электрический ток, который называют фототоком. На основании своих опытов Столетов установил следующие закономерности фотоэффекта: 1) Под действием света вещество теряет только отрицательные заряды; 2) Явление вызывается преимущественно ультрафиолетовыми лучами; 3) Разряжающее действие лучей пропорционально мощности подающего излучения; 4) Разрежающее действие лучей обнаруживается даже при весьма кратковременном освещении, причем между моментом освещения и началом разряда не протекает заметного времени. Фотоэффект практически безынерционен. Было обнаружено, что частицы, испускаемые при фотоэффекте- электроны. Позднее установка Столетова была усовершенствована (рис.2). Эл ектроды были помещены в вакуумный баллон. Свет, проникающий через кварцевое окошко Кв, освещает катод К, изготовленный из исследуемого материала. Электроны, испущенные вследствие фотоэффекта, перемещаются под действием электрического поля к аноду А. В результате в цепи прибора течет фототок, регистрируемый гальванометром. Напряжение между катодом и анодом можно менять помощью потенциометра П. Вольтамперной характеристикой прибора называется зависимость тока, проходящего через прибор от напряжения. на рис.3- Вольтамперная характеристика фотоэффекта. ВАХ снимается при неизменном световом потоке Ф . При некотором напряжении фототок достигает насыщения, все электроны, испущенные катодом, достигают анода. Таким образом, плотность тока насыщения определяется количеством электронов, испускаемых катодом в единицу времени под действием света: , где n – число электронов, вылетающих из катода за 1 секунду, е – заряд электрона, - его скорость. Пологий ход кривой указывает на то, что электроны вылетают из катода с различными по величине скоростями. Часть электронов при отсутствии поля, т.е. при U = 0, обладает скоростями, достаточными для того, чтобы достичь анода без тока. Поэтому при U = 0 сила тока отлична от нуля и равна . Чтобы сила тока стала равна нулю, нужно приложить задерживающее напряжение U₃. При таком напряжении ни один из электронов выбитых с катода, не достигнет анода, т.е. энергия электрона будет полностью израсходована на работу против сил электрического поля, созданного между катодом и анодом: Измерив задерживающее напряжение U₃, можно оценить максимальную кинетическую энергию фотоэлектрона и его максимальную скорость: Не обходимо заметить, что получе­ние точных результатов сильно затрудняют два обстоятельства: 1) экспериментальная кривая I(U) в области U₁ (см. рис. 4) подходит к оси U практически асимптотически, вследствие чего определение U_l довольно неопределенно; 2) всю кривую I(U) смещает (влево или вправо) наличие так называемой контактной разности потенциалов, т. е. разности потенциалов, которая возникает между двумя различными металлами (катод К и анод А изготовляют по необходимости из различных металлов). Причем известно,

• что контактная разность потенциалов между катодом и анодом не зависит от природы проводников, их соединяющих.

• Если контактная разность потенциалов есть и, например, такова, что тормозит вылетающие из катода фотоэлектроны, то приходится прикладывать внешнее напряжение U (измеряемое вольтметром). И если это напряжение таково, что компенсирует тормозящую контактную разность потенциалов, то начало горизонтального участка (тока насыщения) — точка 2 на рис. 4 — сдвинется вправо, в сто­рону положительных значений показа­ния вольтметра U.

Таким образом, задерживающая разность потенциалов U₃ будет равна (по модулю) сумме U₃ = U₂ + |U₁|= U₂ – U₁ (1) как показано на рис. 4, где U₁<0. Заметим, что, вообще гово­ря, U₁ есть величина алгебраическая, она может иметь любой знак или равняться нулю.

• Если контактная разность потенциалов не тормозит, а ускоряет фотоэлектроны, т.е. имеет противоположный знак, то характеристика фотоэлемента I(U) вместе с точкой 2 сместится влево. При этом выражение (1) для U₃ остается прежним, только в нем оба показания вольтметра (U₂ и U₁) могут оказаться отрицательными, но их разность по-прежнему будет положительной и равной U₃.

Итак, определив U₃, мы тем самым находим максимальную кинетическую энергию фотоэлектронов . Отметим, что положение точки 2 на рис. 4, т. е. показание вольтметра U=U₂, зависит только от контактной разности потенциалов, положение же точки 1, т.е. показание U₁ вольтметра — от частоты падающего света. Значит, и задерживающая разность потенциалов U₃ тоже зависит от . Если построить экспериментальный график зависимости E_макс( ), то полу­чается прямая (рис. 5):

• Точка пересечения прямой с осью абсцисс определяет частоту _, соответствующую красной границе фотоэффекта,

• точка пересечения продолжения прямой с осью ординат —работу выхода А.

Если же на оси ординат откладывать U₁, (показание вольт­метра, при котором фототок обращает­ся в нуль), то отмеченные две точки не будут соответствовать ?₀ и А (из-за наличия контактной разности потенциалов). Экспериментально были установлены следующие законы фотоэффекта: 1. Максимальная начальная скорость фотоэлектронов определяется частотой света и не зависит от его интенсивности; 2. Для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота света , при которой фотоэффект еще возможен. Величина зависит от химической природы вещества и состояния его поверхности. 3. Число фотоэлектронов выбиваемых с катода в единицу времени, n, пропорционально световому потоку Ф, падающему на поверхность (или интенсивности света). Это закон Столетова. Классическая физика не смогла объяснить законов фотоэффекта. С ее точки зрения амплитуда колебаний свободного электрона в переменном электрическом поле определяется выражением где m – масса электрона, – частота изменения тока. Электрон, расположенный вблизи поверхности, покинет металл, как только амплитуда его колебаний А превысит некоторое критическое значение. Поэтому из волновой теории следует, что электроны не будут вылетать из металла до тех пор, пока интенсивность падающего света не превысит определенного критического значения. Однако в ходе экспериментальных исследований пороговой интенсивности обнаружено не было. Число вылетающих электронов пропорционально при любой ск оль угодно малой интенсивности. Кинетическая энергия электронов менялась в интервале от 0 до Е_{k max}, и не было электронов с энергией большей Е_{k max}. Изменение кинетической энергии происходит с увеличением частоты падающего света линейно (рис.1.9). Правильное объяснение фотоэффекта дал Эйнштейн в 1905 г.: Свет представляет собой совокупность квантов, каждый из которых обладает энергией = ћ , где ħ – постоянная Планка. Эти кванты (фотоны) ведут себя подобно материальным частицам, при столкновении с электроном в металле фотон может поглотиться, и вся его энергия перейдет к электрону. Планк полагал, что излучение отдается излучающими системами порциями ħ , но само это излучение может иметь любую энергию и поглощаться в любых количествах непрерывно. Эйнштейн же приписал корпускулярные свойства самому излучению, и отдача энергии ħ при излучении объясняется тем простым фактом, что никаких других порций излучения частоты существовать в природе не может. Монохроматическое излучение частоты состоит всегда из целого числа фотонов, энергия каждого из них равна ħ . Такое излучение испускается и поглощается только порциями энергии ħ . При поглощении излучения частоты веществом каждый из электронов может поглотить один фотон, приобретая при этом энергию ħ и никакую другую. Пусть для удаления поверхностного электрона из металла необходимо затратить энергию А, тогда поглотив фотон с энергией ħ и вылетев с поверхности, электрон будет иметь энергию ħ – А. Это и есть максимально возможная кинетическая энергия: (1) величина А называется работой выхода электрона из металла, она зависит от свойств данного металла. Формула (1) представляет собой закон сохранения для фотоэффекта и называется уравнением Эйнштейна для фотоэффекта. Это соотношение согласуется с экспериментальной кривой на рис.1.9. 2.2 Масса и импульс фотона Итак, энергия фотона равна = . Воспользуемся законом взаимосвязи массы и энергии: , где – масса фотона. Отсюда: где с – скорость света в вакууме. Фотон всегда движется со скоростью света, его масса покоя равна нулю. Как всякая частица, фотон обладает массой, энергией и импульсом. Импульс фотона: где ? – длина волны света в вакууме. Так как k = 2?/? то или в векторной форме Связь импульса фотона с его энергией Е_f получена из общей формулы теории относительности: для фотона m₀ = 0 и Импульс фотона – векторная величина, направление импульса совпадает с направлением распространения света, которое характеризуется волновым вектором . Корпускулярные свойства фотона (энергия, импульс и масса) связаны с волновой характеристикой – частотой света . Экспериментальным подтверждением наличия у фотонов массы и импульса является существование светового давления. С квантовой точки зрения давление света вызвано тем, что при соударении с поверхностью тела каждый фотон передает этой поверхности свой импульс.