Связь теплоемкости с термодинамическими функциями

Внутренняя энергия системы может изменяться в результате теплообмена. Т.е., если к системе подводится теплота в количестве dQ, а работа не производится dW = 0, то согласно I закона термодинамики

dU = dQ – dW = dQ

dU = dQ (6.32)

Теплота - способ изменения внутренней энергии системы без изменения внешних параметров (dV = 0 ® dW = 0), это микроскопический способ преобразования энергии.

При поглощении системой некоторого количества теплоты dQ внутренняя энергия ее увеличивается на величину dU (согласно формуле (6.32.)). Возрастание внутренней энергии ведет к увеличению интенсив-ности движения частиц, составляющих систему. Согласно выводам статистической физики средняя скорость движения молекул связана с температурой

Т.е. поглощение системой некоторого количества теплоты dQ ведет к увеличению температуры системы на величину dT, пропорциональную dQ.

dT = const^.dQ (6.33)

Соотношение (6.33) можно переписать в другом виде:

dQ = C^.dT или   , (6.34)

где С – константа, называемая теплоемкостью системы.

Итак, теплоемкость – это количество теплоты, необходимое для нагревания термодинамической системы на один градус по шкале Кельвина.

Теплоемкость системы зависит от:

а) состава и температуры системы;

б) размера системы;

в) условий, при которых происходит переход теплоты.

 

Схема 6.6. Виды теплоемкости

Т.е. С (теплоемкость), как и Q, является функцией процесса, а не состояния и относится к экстенсивным параметрам.

По количеству нагреваемого вещества различают:

1) удельную теплоемкость С_уд, отнесенную к 1 кг или 1 г вещества;

2) молярную (мольную) теплоемкость С_м, отнесенную к 1 моль вещества.

Размерность {С_уд} = Дж/г ^.К

{С_м} = Дж/моль ^. К

Между удельной и молярной теплоемкостями имеется соотношение

С_м = С_уд ^. М, (6.35)

где М – молярная масса.

При описании физико-химических процессов обычно пользуются молярной теплоемкостью С_м (в дальнейшем индекс писать не будем).

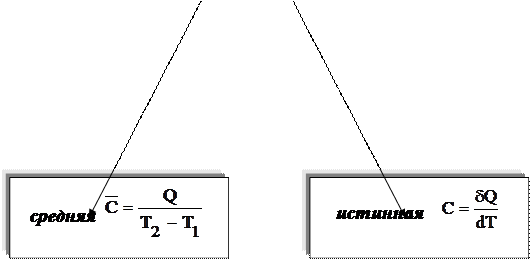
Различают также среднюю и истинную теплоемкости.

Средняя теплоемкость   – это отношение некоторого количества теплоты к разности температур

 (6.36)

Истинной теплоемкостью С называют отношение бесконечно малого количества теплотыdQ, которое нужно подвести к одному моль вещества, к бесконечно малому приращению температуры – dT.

Установим связь между истинной и средней теплоемкостями.

Во-первых, 

Во-вторых, выразим Q из формулы (6.36)   (6.37). С другой стороны из формулы (6.34) ® dQ = CdT (6.38). Проинтегрируем (6.38) в интервале T₁ - T₂ и получим

 (6.39)

Приравняем правые части выражений (6.37) и (6.39)

Отсюда   (6.40)

Это уравнение связывает среднюю теплоемкость   с истинной С.

Среднюю теплоемкость рассчитывают в интервале температур от Т₁ до Т₂. Нередко интервал выбирают от ОК до Т, т.е. нижний предел Т₁ = ОК, а верхний имеет переменное значение, т.е. от определенного интервала перейдем к неопределенному. Тогда уравнение (6.40) примет вид:

 (6.41)

Расчет   можно провести графически, если известны значения истинной теплоемкости при нескольких температурах. Зависимость С = f(T) представлена кривой АВ на рис. 1.

 

Рис. 6.7. Графическое определение средней теплоемкости

 

Интеграл в выражении (6.40) представляет собой площадь фигуры Т₁АВТ₂.

Таким образом, измерив площадь, определяем

 (6.42)

Рассмотрим значение теплоемкости системы при некоторых условиях:

а) V = сonst

Согласно I закону термодинамики dQ_V = dU. Для простых систем внутренняя энергия является функцией объема и температуры U = U (V,T)

Теплоемкость в этих условиях

 (6.43)

б) p = const

dQ_p = dH. Для простых систем H = H(p,T);

Теплоемкость

 (6.44)

С_р и С_V - теплоемкости при постоянных p и V.

Если рассматривать 1 моль вещества т.е. С_р и С_V - молярные теплоемкости

dQ_V = C_VdT, dQ_p = C_pdT (6.45)

Для «n» моль вещества dQ_V = nC_VdT, dQ_p = nC_pdT

 

Исходя из выражения (6.45), находим

 (6.46)

Зная зависимость теплоемкости вещества от температуры, по формуле (6.46) можно вычислить изменение энтальпии системы в интервале Т₁¸Т₂. В качестве базовой температуры выбирается Т₁ = ОК или 298,15 К. В этом случае разность энтальпий Н(Т) – Н(298) называется высокотемпературной составляющей энтальпии.

Найдем связь между С_р и С_V. Из выражений (6.43) и (6.44) можно записать:

Из I закона термодинамики с учетом только механической работы для простой системы, для которой U = U(V,T)

dQ = dU + pdV = 

т.е.   (6.49)

Подставим dQ из выражения (6.46) в (6.48) и (6.49) и получим:

Для простой системы объем можно рассматривать как функцию давления и температуры, т.е.

V = V(p,T) ® dV = 

при условии p = const dp = 0, 

т.е. 

Отсюда   ,

Таким образом   (6.51)

Для 1 моль идеального газа pV = RT, 

 C_p – C_V = 

Для 1 моль реального газа и применение уравнения Ван-дер-Ваальса приводит к следующему выражению:

C_p– C_V= 

Для реальных газов С_p – C_V > R. Эта разность увеличивается по мере увеличения давления, т.к. с увеличением давления растет   , связанное со взаимодействием молекул реального газа друг с другом.

Для твердого тела при обычной температуре С_p – C_V < R и составляет примерно 1 Дж/(моль ^. К). с понижением температуры разность С_p – C_V уменьшается и при Т ® ОК С_p – C_V ® 0.

Теплоемкость обладает свойством аддитивности, т.е. теплоемкость смеси двух веществ

 (6.52)

В общем случае

 ,

где x_i - доля веществ «I» в смеси.

Теплоемкость является одной из важнейших термодинамических характеристик индивидуальных веществ.

В настоящее время имеются точные методы измерения теплоемкости в широком интервале температур. Достаточно удовлетворительно разработана теория теплоемкости для простого твердого вещества при невысоких давлениях. Согласно молекулярно-кинетической теории теплоемкости для одного моль газа на каждую степень свободы приходится R/2. Т.е. поскольку молярная теплоемкость идеального газа при постоянном объеме

C_V = C_n + C_в + C_к + С_э, (6.53)

где C_n – теплоемкость газа, связанная с поступательным движением молекул,

С_в – с вращательным,

С_к – с колебательным,

а С_э – с электронными переходами, то для одноатомного идеального газа С_V = 3/2R,

для двухатомных и линейных трехатомных молекул

C_V = 5/2R + C_к

для нелинейных многоатомных молекул

C_V = 3R + С_к

Теплоемкость С_к, связанная с колебательным движением атомов в молекуле, подчиняется законам квантовой механики и не отвечает закону равномерного распределения энергии по степеням свободы.

С_э в формуле (6.53) не принимается во внимание, С_э – это теплоемкость, связанная с электронными переходами в молекуле. Переход электронов на более высокий уровень под действием теплообмена возможен лишь при температурах выше 2000 К.

Теплоемкость твердых веществ с атомной кристаллической решет-кой можно вычислить по уравнению Дебая:

C_V = C_Д(х),   ,

где q – характеристическая температура;

n_m – максимальная характеристическая частота колебания атомов в молекуле.

При повышении температуры C_V твердых веществ с атомной кристаллической решеткой стремится к предельному значению C_V ® 3R. При очень низких температурах

C_V ~ T³ (T < q/12).

Теплоемкости С_р по опытным значениям C_V (или наоборот) для веществ с атомной кристаллической решеткой можно рассчитать по уравнению:

C_p = С_V (1 + 0,0214C_V   )

Для сложного твердого или жидкого вещества хорошей теории пока не существует. Если экспериментальные данные по теплоемкости отсутствуют, то ее можно оценить с помощью эмпирических правил

1) Правило Дюлонга и Пти: атомная теплоемкость при постоянном объеме для любого простого твердого вещества приблизительно равна 25 Дж/(моль^.К)

Правило выполняется при высоких температурах (близких к температуре плавления твердого вещества) для элементов, атомная масса которых больше, чем у калия. Как показал Больцман, оно может быть качественно обосновано кинетической теорией:

C_V » 25 Дж/(моль^.К)(3R)

2) Правило Неймана-Коппа (правило аддитивности) основывается на предположении о неизменяемости теплоемкости элементов при образовании химических связей

С_св-ва = 25n

где n – число атомов, входящих в молекулу.

Более близкие к экспериментальным значениям теплоемкости получаются по правилу Неймана-Коппа, если принять для легких элементов значения атомных теплоемкостей представленные в табл. 6.1.

 

Таблица 6.1.

Значения атомных теплоемкостей для легких элементов

Элемент	C	H	B	Si	O	F	S	P
Ср0, Дж/(моль.К)	7,53	9,62	11,3	15,9	16,74	20,92	22,59	23,01

 

Для остальных элементов C_p⁰ » 25,94 Дж/(моль^.К).

3) Правило аддитивности лежит в основе формулы Келли, которая справедлива для высококипящих чистых неорганических жидкостей (BeO, BeCl₂, MgBr₂ и др.):

С_р = 32,43n;

где n – число атомов в молекуле, входящих в молекулу неорганического вещества.

У расплавленных элементов с d- и f-электронами С_ат достигает 42¸50 Дж/(моль^.К).

4) Приближенный метод расчета для органических жидкостей, использующий атомно-групповые составляющие теплоемкостей

Последние получены при анализе опытных данных большого числа соединений, некоторые из которых сведены в табл. 6.2.

Таблица 6.2.

Некоторые значения атомно-групповых составляющих теплоемкостей

 

Атом или группа	Ср, Дж/(моль.К)	Атом или группа	Ср, Дж/(моль.К)
–СН3	41,32	–О–	35,02
–СН2–	26,44	–S–	44,35
СН–	22,68	–Cl	35,98
–СN	58,16	–Br	15,48
–ОН2	46,02	C6H5–	127,61
С=О(эфиры)	60,75	–NH2(амины)	63,6
С=О(кетоны)	61,5	–NO2	64,02

 

Зависимость теплоемкости от температуры

 

Теплоемкость твердых, жидких и газообразных веществ повышается с температурой. Только теплоемкости одноатомных газов практически не зависят от Т (например, He, Ar и другие благородные газы). Наиболее сложная зависимость С(Т) наблюдается у твердого вещества. Зависимость С(Т) изучается экспериментально, т.к. теория недостаточно разработана.

Обычно зависимость атомной и молярной теплоемкости от температуры выражается в виде интерполяционных уравнений.

С_р = а + в ^.Т + с ^.Т² (для органических веществ) (6.53)

С_р = а + в ^.Т + с^/ .Т^-2 (для неорганических веществ)

Коэффициенты а, в, с, с^/ - постоянные величины, характерные для данного вещества вычисляются на основании экспериментальных данных и справедливы в определенном интервале температур.

Теплоемкость - ϶ᴛᴏ свойство тел поглощать и выделять теплоту при изменении температуры на один градус в различных термодинамических процессах. Различают общую среднюю и общую истинную теплоемкости.

Общая средняя теплоемкость термодинамического процесса (ТП) - ϶ᴛᴏ теплоемкость тела массой m, кг за конечный отрезок ТП:

 , [Дж/К].

Общая истинная теплоемкость ТП - ϶ᴛᴏ теплоемкость тела массой m, кг в каждый данный момент ТП:

 , [Дж/К].

Рассмотрим произвольный ТП 1-2 в координатах   , где Q – подведенная теплота в [Дж]; t – температура в [⁰C]. Тогда   ,   .

В случае если ТС – однородное рабочее тело, то в расчетах применяются относительные теплоемкости:

- удельная теплоемкость – теплоемкость, отнесенная к 1 кг вещества с=С/m, Дж/кгК;

- молярная теплоемкость – теплоемкость, отнесенная с 1 молю вещества   , Дж/мольК;

- объёмная теплоемкость – теплоемкость, отнесенная к 1м³ вещества   , Дж/м³К.

Теплоемкость – функция процесса и зависит от рода рабочего тела, характера процесса и параметров состояния. Так, теплоемкость в процессе с постоянным давлением принято называть изобарной теплоемкостью:

 ,

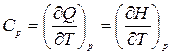где H, Дж – энтальпия.

Теплоемкость в процессе с постоянным объёмом принято называть изохорной теплоемкостью:

 ,

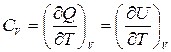где U, Дж – внутренняя энергия.

Теплоемкость идеального газа не зависит от температуры и давления и зависит только от числа степеней свободы движения молекул и в соответствии с законом о равном распределœении энергии по степеням свободы движения молекул теплоемкость:   , где   - вращательные степени свободы, равные для одноатомного газа нулю   , для двухатомного газа -   =2 и для трехатомных газов   =3;   Дж/мольК – молярная газовая постоянная. Теплоемкость   определяется по уравнению Майера:

 .

Для одноатомного газа   и   , для двухатомного газа   и   , для трех и более атомных газов   и   .

Теплоемкость реальных газов зависит от давления и температуры. В ряде случаев можно пренебречь влиянием давления на теплоемкость и принять, что теплоемкость реальных газов зависит только от температуры: C=f(t). Эта зависимость определяется экспериментально.

Эмпирическая зависимость удельной истинной теплоемкости от температуры должна быть представлена в виде многочлена:

 , Дж/кгК,

где   при температуре t=0⁰C. Для двухатомных газов можно ограничиться двумя слагаемыми:   , или   , где   .

Для конечного участка процесса 1-2 количество теплоты равно:

 .

Тогда средняя теплоемкость на этом участке процесса будет равна:

 , Дж/кгК.

В области низких температур при Т<100К прекращается вращательное движение молекул и колебательное движение атомов, а при температуре Т→0К прекращается и поступательное движение молекул, ᴛ.ᴇ. при Т=0К С_р=C_v=0 и прекращается тепловое движение молекул (опытные данные Нернста и др., 1906-1912гᴦ.). При температуре Т→0К свойства веществ перестают зависеть от температуры, как это иллюстрируется на приведенном графике зависимости теплоемкости от абсолютной температуры.