9.3. Работа газа при его расширении

Рассмотрим сжатие идеального газа, находящегося под поршнем (рис.9.1). Под действием внешней силы переместим поршень на бесконечно малую величину , настолько малую, что будем считать силу постоянной. Назовём работу постоянной силы по перемещению поршня на бесконечно малую величину элементарной работой и обозначим . Элементарная работа может быть определена как работа постоянной силы через скалярное произведение силы на перемещение:

(9-6)

Поскольку направление силы и перемещения совпадают, то . Газ, находящийся под поршнем, препятствует сжатию и давит на поршень силой , равной по величине, противоположной по направлению и приложенной к поршню (рис.4.1). Элементарная работа самого газа . Так как сила и перемещение направлены в противоположные стороны, работа самого газа при равномерном сжатии отрицательна и равна по величине работе внешней силы, сжимающей газ . Сила, действующая на единицу площади поверхности поршня S со стороны газа, есть давление газа Р. Поэтому можно выразить величину силы через давление: . Тогда элементарная работа газа будет равна: . Но есть величина приращения объёма газа. Тогда элементарная работа газа равна:

, (9-7)

а работа внешней силы по сжатию газа равна .

Для определения работы по перемещению поршня на значительную величину , в результате которой объём газа изменяется на , нужно учесть процесс, происходящий с газом. Работу в этом случае определяют через интеграл:

(9-8)

Работа газа (или над газом) зависит от процесса (т.е. от последовательности промежуточных состояний) и поэтому является функцией процесса. Работа не является полным дифференциалом, отсюда и обозначение элементарной работы , а не dA.

Рассмотрим работу, совершаемую газом, при различных процессах. Будем обозначать в дальнейшем элементарную работу газа просто через и считать её положительной, если газ расширяется ( ), и отрицательной, если газ сжимают ( ).

Рассмотрим изохорический процесс. При изохорическом процессе объём газа не изменяется, приращение объёма равно нулю, следовательно, работа газа равна нулю.

Поскольку работу в любом случае можно определить, пользуясь формулой (9-8), для математической интерпретации работы удобно изображать любой процесс на диаграмме (P,V) . Работа на такой диаграмме равна площади фигуры под кривой, изображающей тот или иной процесс, происходящий с газом.

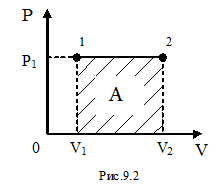
Рассмотрим изобарический процесс (рис. 9.2). Используя формулу (9-8) найдём работу газа при переходе из состояния 1 в состояние 2: .

Так как для данного количества вещества давление остаётся постоянным при изобарическом процессе, то его можно вынести за знак интеграла, тогда получим :

. Обозначим . С учётом этой записи работа при изобарическом процессе определяется по формуле:

(9-9)

Используя рис.9.2, можно записать работу через указанные параметры состояния: . Такую же формулу мы получим, находя площадь заштрихованного прямоугольника. Часто бывает удобно выражать работу через изменение температуры. Для этого нужно использовать уравнение состояния идеального газа (уравнение Менделеева – Клапейрона) для 1 и 2 состояний: и . Вычитая из второго уравнения первое, получим:

(9-10)

При изобарическом сжатии конечный объём меньше начального и работа газа отрицательна, то есть газ препятствует сжатию.

Формула (9-7) позволяет выразить физический смысл молярной постоянной R . Для одного моля вещества ( ) работа определяется как . Отсюда ясен физический смысл R , которая определяется работой изобарического расширения одного моля идеального газа при изменении температуры на один кельвин.

Рассмотрим изотермический процесс (рис.9.3). При изотермическом процессе температура остаётся постоянной, а давление и объём связаны между собой обратно пропорциональной зависимостью. В этом случае, используя формулу (9-8) для определения работы, уже нельзя вынести давление за знак интеграла. Давление выразим из уравнения Менделеева – Клапейрона: . Подставим правую часть этого уравнения в (9-8) и вынесен за знак интеграла все постоянные:

. Учитывая, что разность логарифмов есть логарифм отношения, получим:

(9-11)

Используя закон Бойля- Мариотта: , можем выразить работу и через отношение давлений:

(9-12)

Рассмотренные примеры подтверждают, что работа является функцией процесса.

Первое начало термодинамики

Первое начало термодинамики учитывает энергетический баланс системы. В этом суть первого начала термодинамики. Можно сказать, что первое начало термодинамики является законом сохранения энергии для термодинамических систем.

Для элементарного процесса первое начало термодинамики можно записать следующим образом: . Работа самого газа связана с работой внешних сил равенством . Тогда математическая запись первого начала термодинамики будет иметь вид: . Однако в тех случаях, когда происходит теплообмен и система получает (или отдаёт тепло), удобно записывать первое начало в виде:

(9-13)

Распределение энергии по степеням свободы молекулы

Чтобы разобраться в связи температуры с внутренней энергией, повторим введенное ранее в механике понятие — число степеней свободы.

Число степеней свободы механической системы — это минимальное число независимых скалярных величин, задание значений которых необходимо для однозначного определения конфигурации системы.

В § 1.3 было показано, что давление газа численно равно импульсу, который передается за единицу времени единице площади стенки в результате ударов по ней молекул, поэтому давление определяется средней энергией только поступательного движения молекул.

Поступательное движение любой системы «как целого» полностью определяется движением одной единственной точки: её центра масс. В частности, полный импульс  любой нерелятивистской системы, равен произведению массы  этой системы на скорость  движения её центра масс. Энергия поступательного движения системы «как целого» равна . Поэтому, для полного описания поступательного движения любой системы в трехмерном пространстве необходимо и достаточно задание значений трех координат центра масс. Таким образом, поступательному движению, как бы ни была устроена система, всегда соответствуют  три поступательных степени свободы: .

Можно сказать и так: «с точки зрения поступательного движения» любая система может быть точно, а не приближенно, представлена в виде одной единственной материальной точки совпадающей с центром масс системы и имеющей массу равную массе системы (рис. 1.15).