2.5 Випадкові процеси та їх загальні характеристики

Випадковим процесом (ВП) називається така функція часу (зміна напруги, струму в електричному ланцюзі або іншої фізичної величини), значення якої в результаті досліду може бути визначене у будь-який момент часу з вірогідністю менше одиниці. Відмітимо, що для детермінованого (регулярного) процесу (сигналу) всі його значення (параметри) визначаються у будь-який момент часу з вірогідністю, рівній одиниці.

Випадковий процес X(t) може приймати різні конкретні форми в результаті досліду, які називають його реалізаціями x_i(t). Приклади реалізації випадкового процесу приведені на рис.2.17. Сукупність реалізацій випадкового процесу називається його ансамблем. У деякий фіксований момент часу t₁ різні реалізації процесу X(t) приймають конкретні різні значення x₁(t₁), x₂(t₂)., x_N(t₁). При цьому всі реалізації x_i(t) є детермінованими. Сукупність значень X(t₁) є випадковою величиною і називається перетином випадкового процесу.

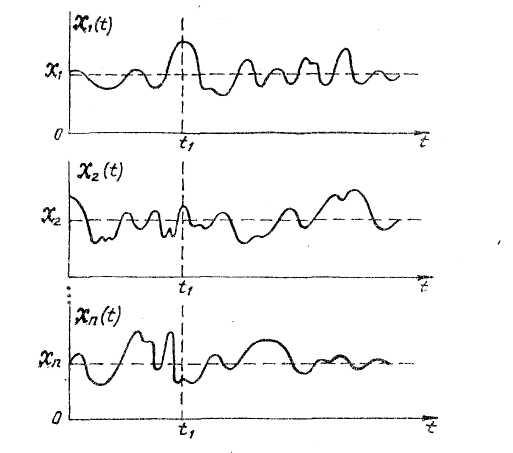
Рисунок 2.17 - Приклади реалізацій випадкового процесу X(t)

2.5.1 Функції розподілу випадкових процесів

Оскільки випадковий процес (сигнал) описується випадковою функцією часу, значення якої при будь-якому значенні аргументу (часу) є випадковими величинами, то його можна задати (описати) тільки в імовірнісному сенсі. Для цієї мети використовується математичний апарат теорії вірогідності, математичної статистики і теорії випадкових процесів.

Якщо визначені всілякі реалізації для n-перетинів випадкового процесу, то його можна описати n-мірною інтегральною функцією розподілу (ІФР) вірогідності (інтегральним законом розподілу вірогідності), яка записується у вигляді

.

Тут вираз означає вірогідність того, що випадкова величинаX(t₁) для першого перетину випадкового процесу X(t) не перевищує заданого фіксованого значення (рівня) х₁ і т.д.

Якщо існують всі приватні похідні від інтегральної функції розподілу вірогідності F_n по кожному з аргументів x₁,x₂,...,x_n, то можна визначити n-мірну диференціальну функцію розподілу (ДФР) вірогідності випадкового процесу (диференціальний закон розподілу вірогідності), звану також функцією щільності розподілу вірогідності, яка в кожному з n-перетинів в моменти часу t₁,t₂,…,t_n характеризує вірогідність попадання значень випадкового процесу в нескінченно малий інтервал. Тоді цю функцію можна записати у вигляді

.

Функція розподілу вірогідності F_n і w_n повністю описують конкретний випадковий процес, проте на практиці достатньо знати двомірні або одномірні функції розподілу вірогідності, хоча вони характеризують випадковий процес тільки в двох або в одному його перетинах.

Так, двомірна інтегральна функція F₂(x₁,x₂;t₁,t₂) визначається як вірогідність того, що випадкова величина X(t₁) не перевищить значення x₁, а випадкова величина X(t₂) не перевищить значення x₂ і записується у вигляді

.

Двовимірна щільність розподілу вірогідності визначається як частна похідна (якщо вона існує) другого порядку від двомірної інтегральної функції розподілу відповідно до виразу

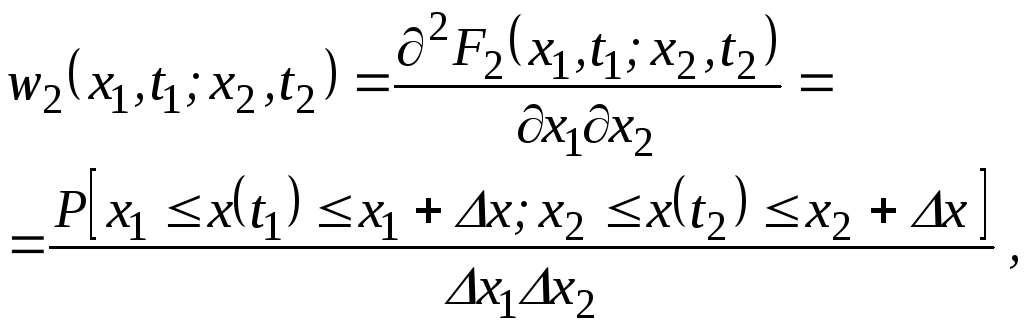
де

Двомірні функції розподілу вірогідності дозволяють оцінювати розвиток випадкового процесу в часі (між двома перетинами).

Одномірна інтегральна функція розподілу визначається як вірогідність того, що у момент часу t₁ випадкова величина Х(t₁) не перевищить значення х₁ і записується у вигляді

.

Одномірна щільність розподілу вірогідності ВП визначається як часна похідна від інтегральної функції розподілу з виразу

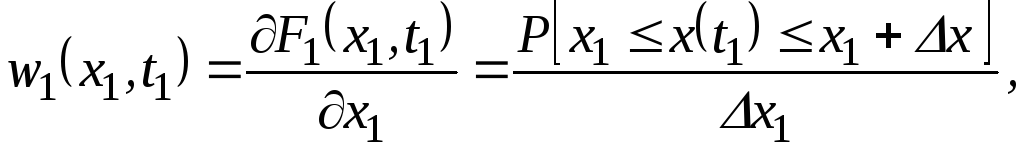
де .

Вона характеризує вірогідність знаходження (попадання) випадкової величини Х(t₁) в інтервалі значень випадкового процесу в перетиніХ(t₁).

Таким чином, одномірні функції розподілу не дозволяють оцінити розвиток випадкового процесу в часі.

На підставі вищевикладеного можна вказати на наступні властивості функцій розподілу випадкових процесів.

Інтегральна функція розподілу вірогідності є безрозмірною, невід’ємною і змінюється від 0 до 1.

Диференціальна функція (щільність) розподілу вірогідності також є невід’ємною, має розмірність зворотну величині і змінюється від 0 до ∞.

Площа під кривій щільності розподілу вірогідності рівна

. (2.81)

Вираз (2.81) визначає властивість нормування щільності розподілу вірогідності.