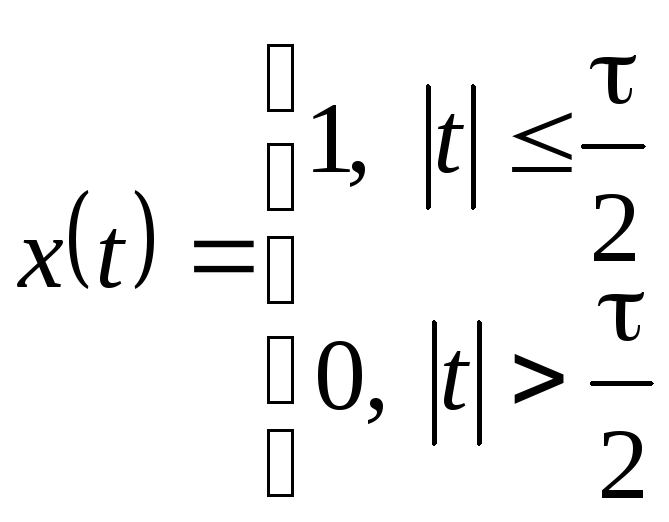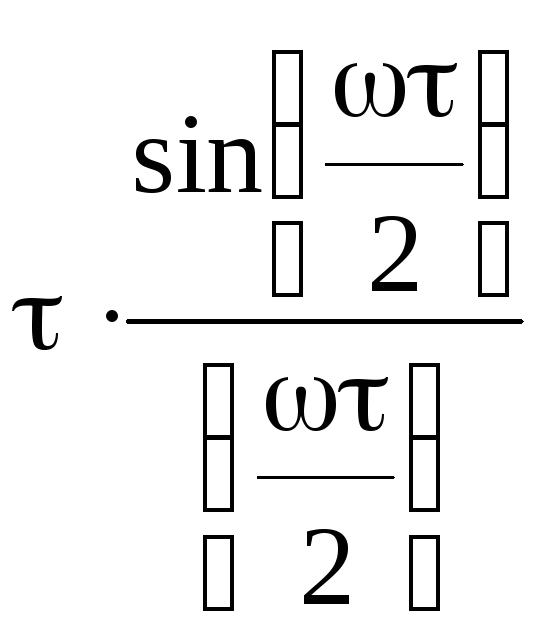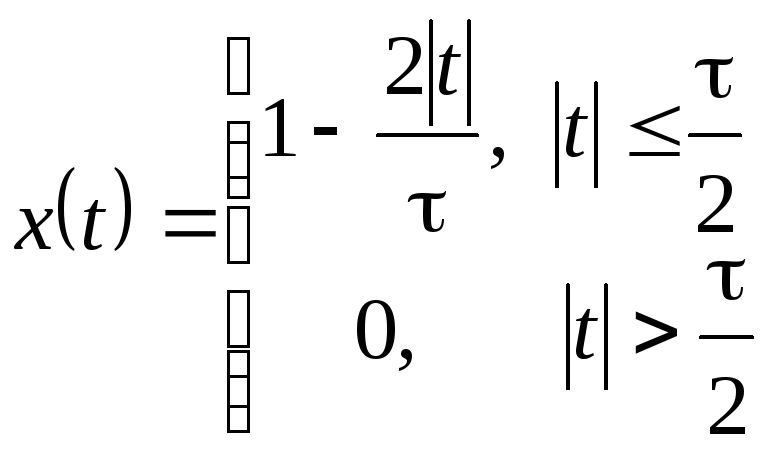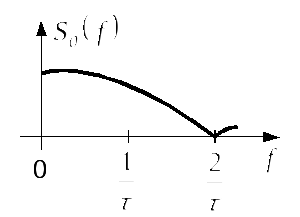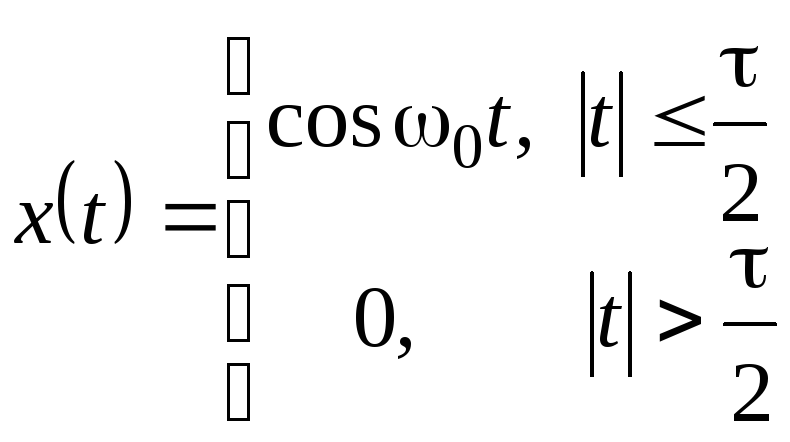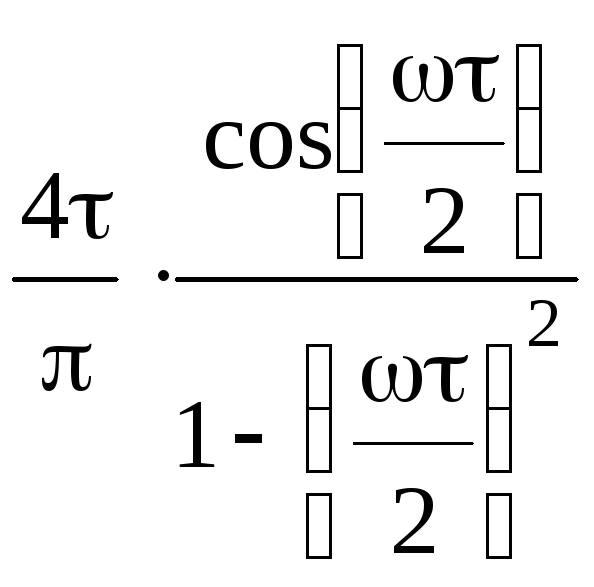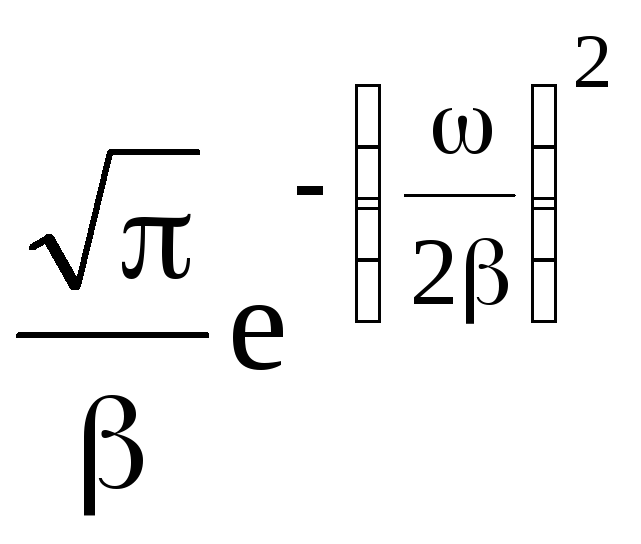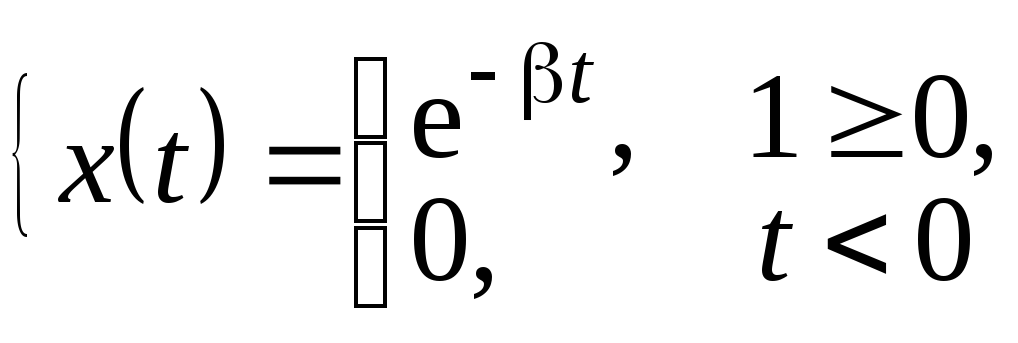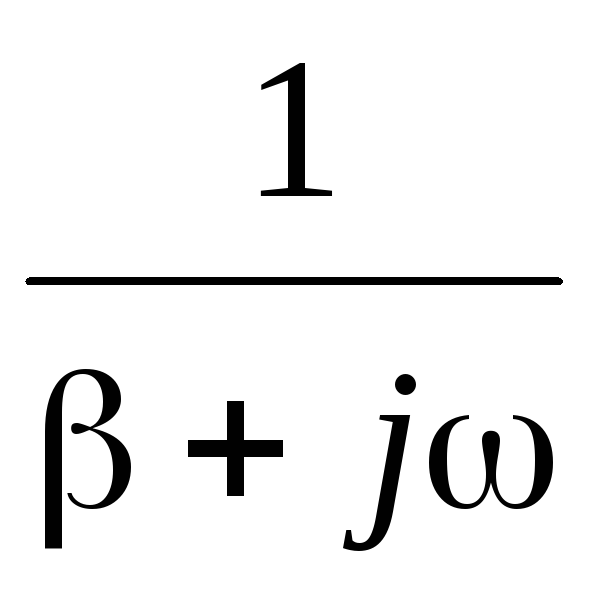2.2.2 Спектральне представлення неперіодичних сигналів

Розкладання в тригонометричний ряд Фур'є (2.29) може бути узагальнене для випадку неперіодичних сигналів при спрямуванніабо. Для цього запишемо (2.29) у наступному вигляді:

, (2.32)

де – частотний рознос між лініями спектра періодичного сигналу.

Розглянемо поточну частоту спектра і визначимо спектральну щільність (СЩ) за Фур'є для неперіодичного сигналу:

. (2.33)

Тоді з (2.32) при отримаємо вираз

, (2.34)

а з (2.30) і (2.33) тоді формула для визначення СЩ буде мати наступний вигляд

. (2.35)

Згідно (2.34) неперіодична функція має вигляд суми гармонійних компонентів (на додатних і від’ємних частотах) з нескінченно малими амплітудами . Модуль визначає неперервний спектр неперіодичного сигналу, a – безперервний фазовий спектр неперіодичного сигналу. Спектр по Фур'є можна записати як

,

де – парна функція частоти (2.36,а); – непарна функція частоти. (2.36,б)

З виразів (2.36 а,б) видно, що для дійсних функцій амплітудний спектр– є парною функцією частоти, фазовий спектр– непарна функція частоти.

Дискретний (лінійчатий) спектр амплітуд періодичного сигналуз урахуванням (2.30) можна знайти за формулою

. (2.37)

Перетворення Фур'є (пряме і (зворотне) описуються, як видно з (2.32) і (2.33), лінійним оператором. Тому для цих перетворень справедливий принцип суперпозиції (накладення): СЩ для сигналу визначається сумою СЩ доданків. Варто підкреслити, що, строго кажучи, СЩ (2.33) існує для сигналів, які задовольняють умові абсолютної інтегрованості

. (2.38)

Проте можна визначити СЩ і для сигналів , що не задовольняють умові (2.38), якщо скористатися введеною вищеузагальненою -функцією. Наприклад, нехай , тоді СЩ за Фур'є такого сигналу за визначенням знаходиться з виразу

. (2.39)

Скориставшись інтегральним визначенням -функції з (2.39) одержимо результат. Аналогічно можна показати, що СЩ для сигналу дорівнює .

Як наслідок цього, СЩ для сигналу набуде вигляду, спектральна щільність для сигналузапишеться формулою .

Скалярний добуток функцій і(у загальному випадку комплексних) у просторі Гілбертаможна виразити і через їхній СЩ за Фур'є:

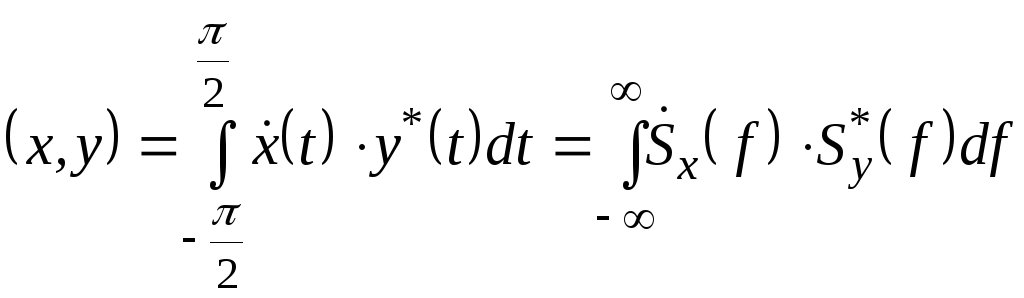. (2.40)

Співвідношення (2.40) називають узагальненою формулою Релея (або рівністю Парсеваля).

Якщо в (2.40) припустити, що , то для дійсного сигналумаємо

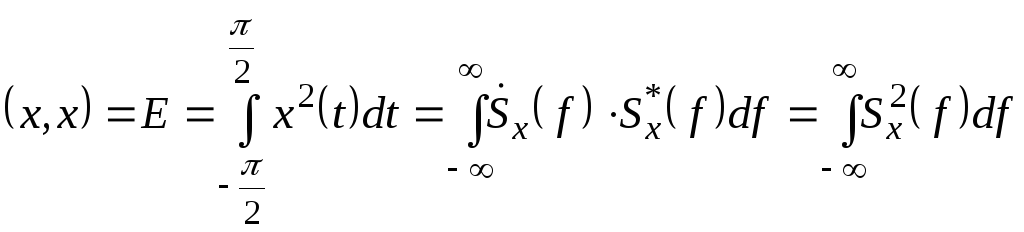. (2.41)

Характеристика маєсмисл СЩ енергії, і вираз (2.41) можна записати у такому вигляді:

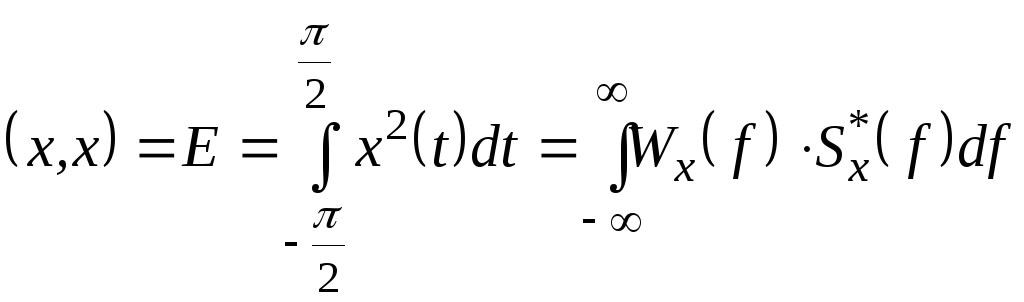. (2.42)

Можна також ввести поняття спектральної щільності потуж­ності (СЩП) сигналу тривалістю :. Тоді вираз для потужності сигналу з (2.42) запишеться як

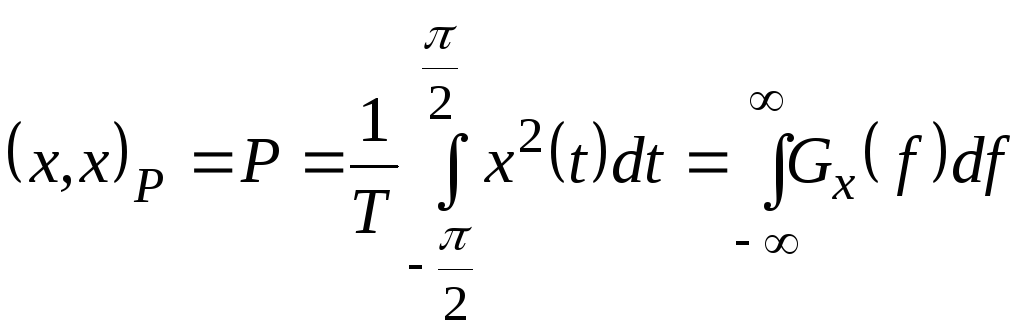. (2.43)

Характеристики івідіграють важливу роль у перетворенні сигналів і їхніх спектрів. З їхнього визначення ясно, що ці характеристикиє парними функціями частоти. Тоді вираз для енергії і потужності сигналу запишемо у вигляді

; (2.44)

, (2.45)

де і– відповідно СЩ енергії і потужності, визначені на частотах.

Співвідношення (2.43) корисно узагальнити. Визначимо скалярний добуток і запишемо у наступному вигляді

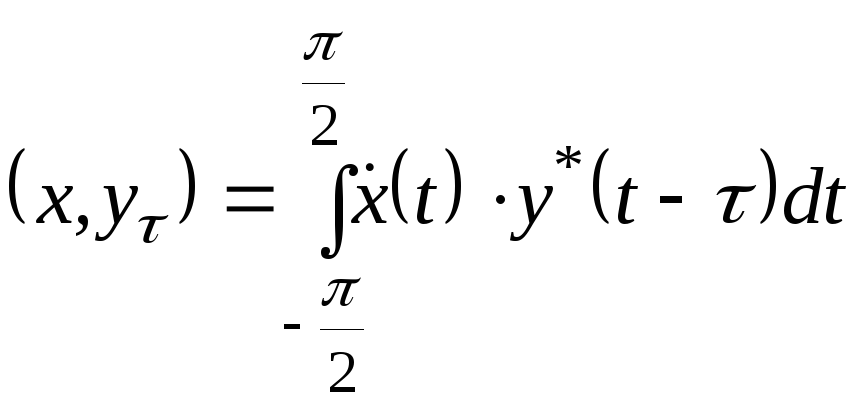. (2.46)

Враховуючи, що спектр Фур'є для затриманого на час сигналу дорівнює, а для сигналу спектр Фур'є дорівнює, одержуємо з (2.46) співвідношення

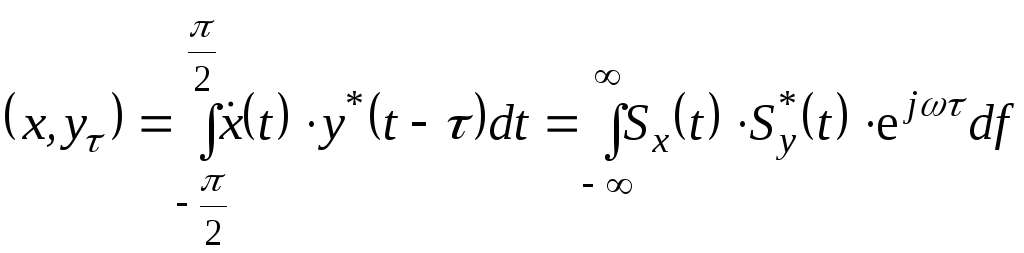. (2.47)

Якщо в (2.47) припустити і ввести позначеннядля функції кореляції (ФК) сигналуз розмірністю енергії, то можна записати

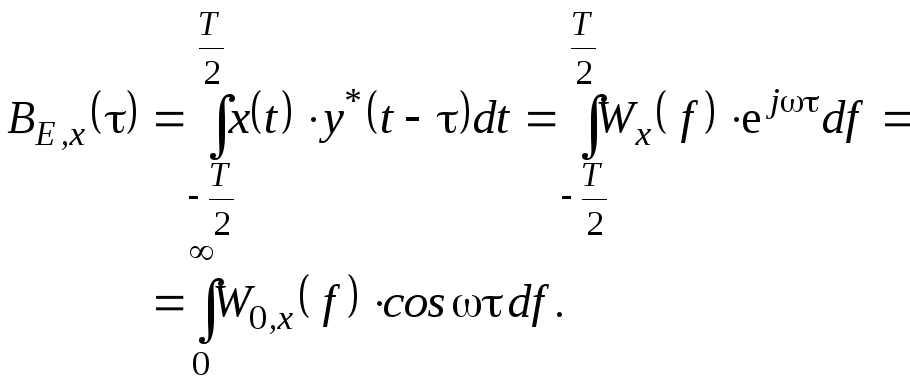(2.48)

Ввівши позначення для ФК сигналуз розмірністю потужності, одержуємо співвідношення

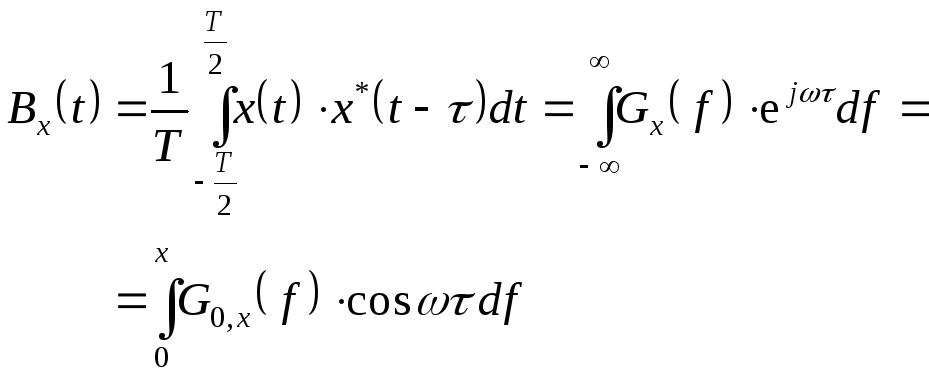
(2.49)

і, як наслідок перетворень Вінера-Хінчина отримаємо [20]:

; (2.50,а)

. (2.50,б)

Таким чином, ФКсигналуі його СЩ потужності(аналогічно ФК сигналу і його СЩ енергії) утворять пари перетворень Фур'є.

В табл. 2.1, для ілюстрації, наведені приклади спектрів деяких імпульсів (неперіодичних функцій) і дані графіки їхніх амплітудних спектрів в області додатних частот. З наведених прикладів видно, що імпульси обмеженої тривалості теоретично мають нескінченний спектр. Практично під шириною спектра будемо розуміти ефективну область частот , у межах якої сконцентровано 90...99% енергії.

Для гаусового і експонентного імпульсів, що мають теоретично нескінченну тривалість, для зручності розрахунків також вводять поняття ефективної тривалості , розуміючи під цим інтервал часу, у межах якого зосереджена основна частка енергії сигналу. Якщо прийняти за основну частину всієї енергії сигналу, то ефективна ширина спектра й ефективна тривалість відповідно знаходяться з виразів

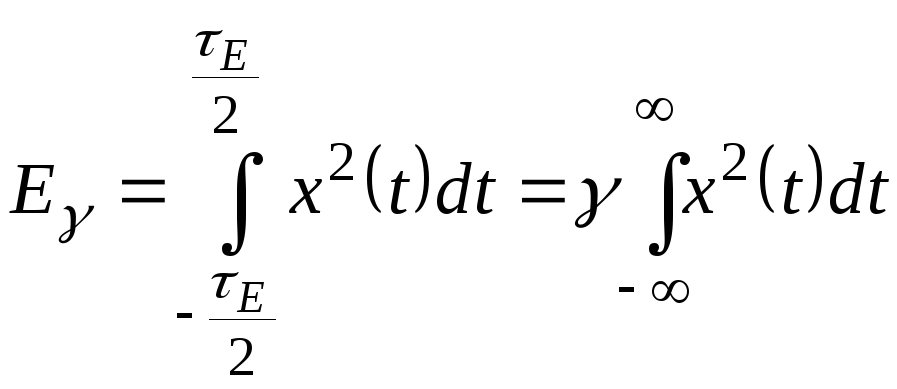та .

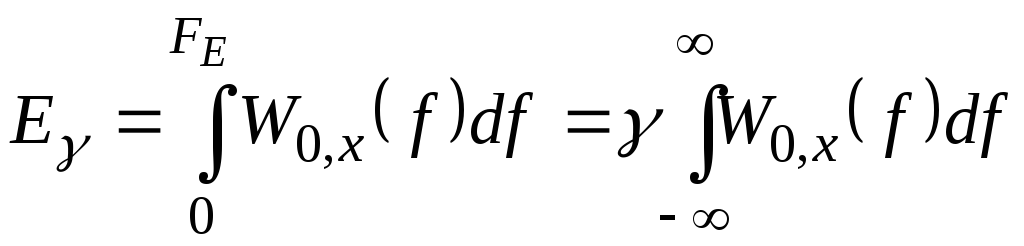Характерною рисою є те (табл. 2.1), що для всіх імпульсів (простих сигналів) виконується співвідношення ,тобто добуток – величина порядку одиниці. Це співвідношення вказує на явний зв'язок між шириною спектра і тривалістю імпульсу: чим коротший імпульс, тим ширший його спектр.

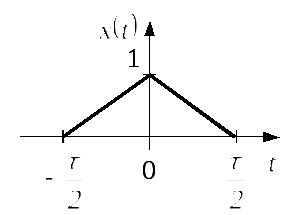
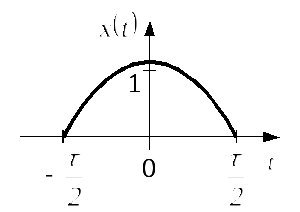
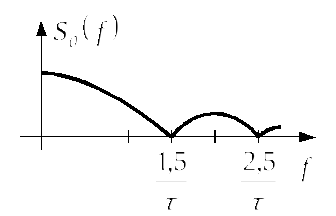
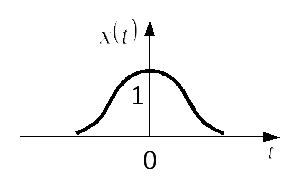
Таблиця 2.1 – Спектри імпульсів різної форми при

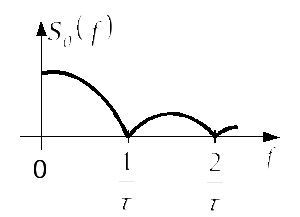
№ п/п	Сигнал		Спектральна щільність	Амплітудний спектр
1
2
3
4
5

Для порівняння в табл. 2.2 наведені значення добутків придля імпульсів з табл. 2.1.

_{Таблиця 2.2 – Характеристики імпульсних сигналів}

№ п/п	Імпульс
1	Прямокутний			0,73
2	Трикутний			0,46
3	Косинусоїдальний			0,43
4	Гаусовий			0,22
5	Експонентний			1,13

Для складних сигналів з базою виконується нерівність.