2.5.4.2 Кореляційні функції випадкових процесів (сигналів)

Кореляційна (автокореляційна) функція випадкового процесу X(t) встановлює ступінь статистичного зв'язку миттєвих значень процесу, узятих в різні моменти часу. Для центрованого нестаціонарного випадкового процесу вона визначається як математичне очікування добутку двох значень процесу в двох різних його перетинах при t₁ і t₂:

(2.98)

де - двовимірна щільність вірогідності розподілу миттєвих значень випадкового процесуX(t). Автокореляційна функція для нецентрованого нестаціонарного процесу X(t), звана коваріаційною, визначається з виразу:

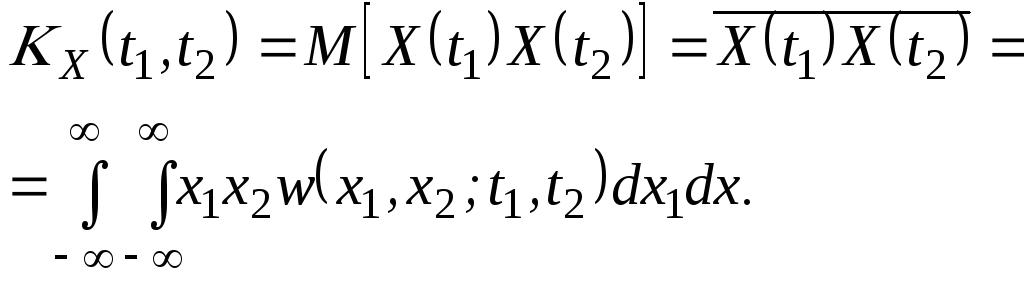(2.99)

З виразів (2.98) і (2.99) виходить, що кореляційна і коваріаційна функції випадкового нестаціонарного процесу залежать як від вибору його перетину (моментів часу t₁, t₂), так і від різниці моментів часу τ = t₂-t₁.

Між кореляційною і коваріаційною функціями існує наступний зв'язок:

. (2.100)

Звідси витікає, що .

При вираз (2.100) визначає дисперсію випадкового процесу у момент часу:

.

Для стаціонарного випадкового процесу Х(t) в широкому сенсі автокореляційна функція визначається з виразу:

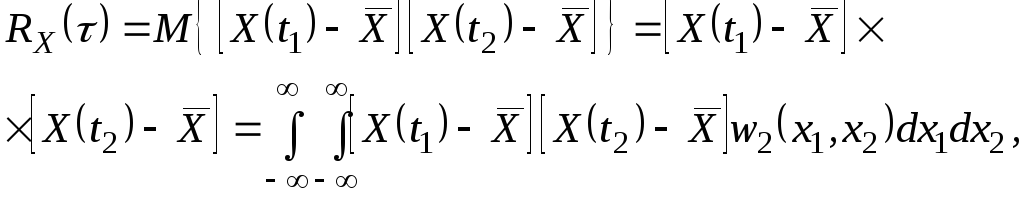(2.101)

а коваріаційна функція знаходиться з виразу:

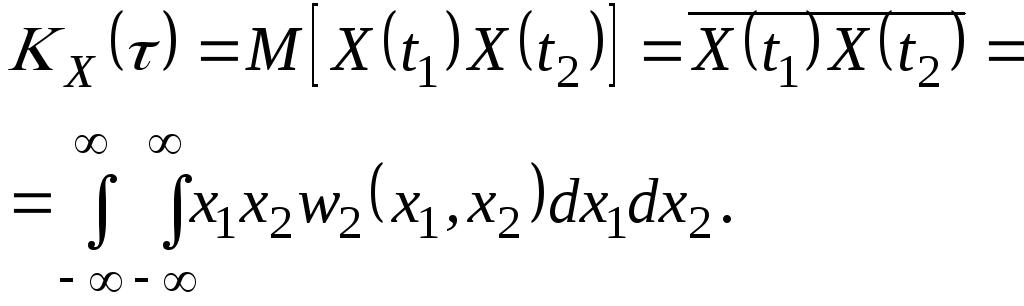(2.102)

З виразів (2.101) і (2.102) виходить, що кореляційна і коваріаційна функції стаціонарного випадкового процесу не залежать від вибраних перетинів (моментів часу t₁ і t₂), і залежать від різниці моментів цих перетинів. Примаємо:

,

тобто кореляційна функція даного процесу, визначена для одного будь-якого перетину, рівна дисперсії процесу D_Х або квадрату середньоквадратичного відхилення значень випадкового процесу від середнього значення.

Дисперсію можна також знайти з виразу:

.

Для ергодичного стаціонарного випадкового процесу вираз АКФ записується у вигляді:

,

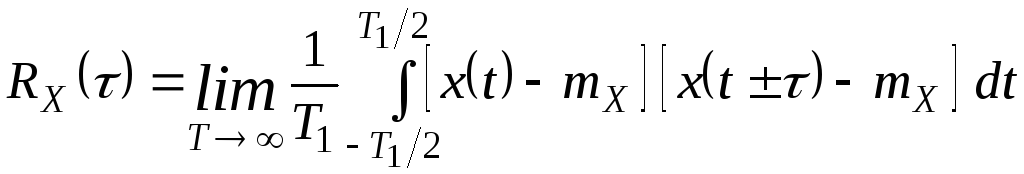де m_X – математичне очікування випадкового процесу.

Вираз для коваріаційної функції процесу має вигляд:

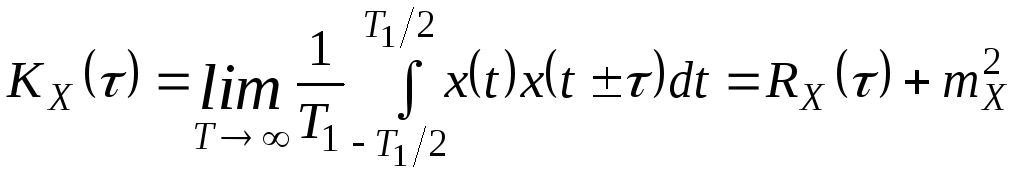
Нормована АКФ стаціонарного ергодичного випадкового процесу визначається з виразу:

а нормована коваріаційна функція знаходиться з виразу:

Інтервал кореляції τ_k для випадкового процесу визначається найбільшим часовим інтервалом між двома перетинами процесу , в межах якого значення функції кореляції зменшується до певного значення, наприклад, до.

2.5.4.3 Взаємні кореляційні функції різних випадкових процесів (сигналів)

Для оцінки статистичного зв'язку двох випадкових процесів Х(t) і Y(t) вводиться поняття взаємної кореляційної функції (ВКФ).

Для нестаціонарних центрованих випадкових процесів вираз ВКФ має вигляд:

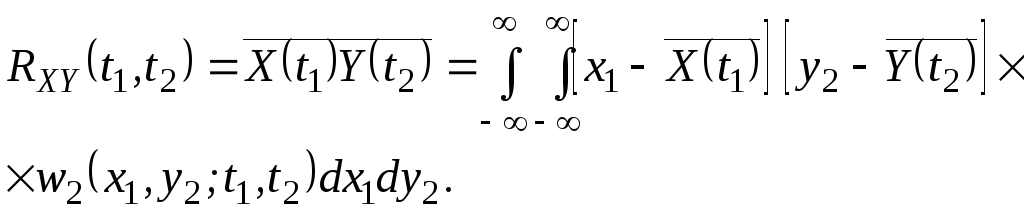(2.103)

Вираз для взаємної коваріаційної функції записується у вигляді:

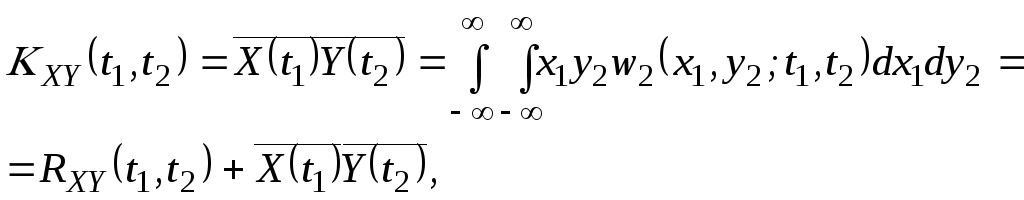(2.104)

де - двовимірна щільність розподілу вірогідності миттєвих значень випадкових процесівХ(t) і Y(t).

Нормовані ВКФ визначаються з виразів:

, (2.105)

, (2.106)

де і- відповідно середньоквадратичне значення випадкових процесівХ(t) і Y(t) в моменти часу t₁ і t₂.

Для стаціонарних в широкому сенсі випадкових процесів вирази (2.103), (2.104), (2.105) і (2.106) запишуться у вигляді:

(2.107)

(2.108)

, (2.109)

. (2.110)

При маємо,,.

Враховуючи, що , отримаємо

Для ергодичних стаціонарних незалежних випадкових процесів вирази (2.107) і (2.108) запишуться у вигляді:

, (2.111)

, (2.112)

, (2.113)

де m_Xm_Y – відповідно математичне очікування випадкових процесів Х(t) і Y(t).

Для ергодичного стаціонарного випадкового процесу виконуються умови:

Інтервал кореляції для взаємної функції кореляції визначається максимальним значенням часового зсуву випадкового процесуХ(t) відносно процесу Y(t) (або навпаки), при якому значення ВКФ досягає, наприклад, 0,1 від свого максимуму.