
- •Глава 2математичні моделі повідомлень, сигналів і завад
- •2.1 Функціональні простори і їх базиси
- •2.2 Спектральний аналіз сигналів на основі рядів Фур'є
- •2.2.1 Спектральне представлення періодичних сигналів
- •2.2.2 Спектральне представлення неперіодичних сигналів
- •2.3 Ортогональні функції Радемахера і Уолша
- •2.4 Дискретизація в часі безперервних сигналів і їх відновлення
- •2.4.1 Дискретизація безперервних сигналів
- •2.4.2 Спектральне уявлення дискретизованих сигналів
- •2.4.3 Особливості дискретизації сигналів
- •2.4.5 Відновлення безперервного сигналу
- •2.5 Випадкові процеси та їх загальні характеристики
- •2.5.1 Функції розподілу випадкових процесів
- •2.5.2 Моментні (числові) характеристики випадкових процесів
- •2.5.3 Приклади деяких випадкових процесів
- •2.5.3.1 Сукупність гармонійних коливань з випадковою амплітудою
- •2.5.3.2 Сукупність гармонійних коливань з випадковими фазами
- •2.5.3.3 Гаусовий (нормальний) випадковий процес
- •2.5.3.4 Сума гармонійних реалізацій з випадковими фазами нормального гаусового шуму
- •2.5.3.5 Розподілення Пуассона
- •2.5.3.6 Експоненціальне розподілення
- •2.5.4 Кореляційні функції детермінованих і випадкових процесів
- •2.5.4.1 Кореляційні функції детермінованих сигналів
- •2.5.4.2 Кореляційні функції випадкових процесів (сигналів)
- •2.5.4.3 Взаємні кореляційні функції різних випадкових процесів (сигналів)
- •2.5.4.4 Зв'язок між кореляційною функцією стаціонарного випадкового процесу і його спектральною щільністю потужності
- •2.6 Аналітичний вузькосмуговий сигнал
- •2.6.1 Математичні моделі і характеристики аналітичного сигналу
- •2.6.2 Імовірнісні характеристики огинаючої і фази вузькосмугового випадкового гаусового процесу
- •2.7 Марковські процеси
2.5.3.6 Експоненціальне розподілення
Для випадкових точкових процесів з розподіленням Пуассона (2.90) величина τ, що визначає інтервал між викликами (рис.2.32), описується експоненціальним розподіленням з одномірною щільністю розподілу вірогідності (ЩРВ) вигляду
![]() . (2.92)
. (2.92)
Графік цієї функції представлений на рис.2.32,а.
Тоді вираз для одномірної ІФР (рис.2.32,б) запишеться у вигляді
![]() .
(2.93)
.
(2.93)
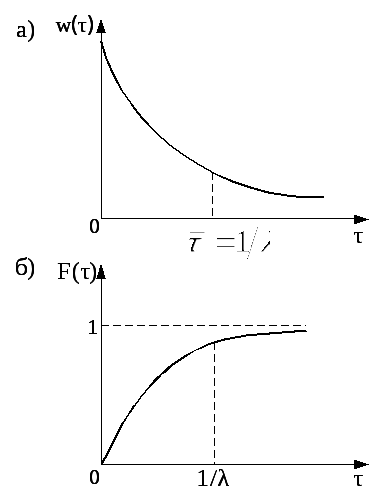
Рисунок 2.32 - Графіки функцій ЩРВ (а) і ІФР (б) для експоненціального розподілення дискретної величини
Таким чином, за допомогою виразів (2.92) і (2.93) можна знайти, наприклад, вірогідність того, що інтервал між сусідніми викликами виявиться рівним або менше деякого значення τ0. Ці вирази також використовуються при визначенні ЩРВ інтервалу між двома відмовами (несправностями) в роботі пристрою.
2.5.4 Кореляційні функції детермінованих і випадкових процесів
Для дослідження характеристик сигналів при їх перетворенні в різних функціональних елементах і пристроях засобів зв'язку окрім спектрального аналізу широко застосовується кореляційний аналіз. Він дозволяє без аналізу спектру сигналу визначати його основні характеристики і параметри, а також швидкість (частоту) зміни (убування або зростання) якого-небудь параметра сигналу.
Слово «кореляція» означає зв'язок між сигналом S(t) і його копією S(t-τ), зрушеною щодо початкового сигналу на інтервалі τ, або між якими-небудь перетинами випадкового процесу.
Оскільки детерміновані сигнали є реалізаціями випадкових процесів, то спочатку розглянемо кореляційні функції детермінованих сигналів.
2.5.4.1 Кореляційні функції детермінованих сигналів
Кореляційною функцією детермінованого сигналу називається функція, що визначає зв'язок між сигналом і його копією, зсунутою по осі часових зсувів на інтервал τ.
Для неперіодичних детермінованих сигналів кореляційна функція, звана також автокореляційною (АКФ), визначається з виразу:
![]() .
(2.94)
.
(2.94)
Вираз
(2.94) указує на те, що АКФ сигналу при
зсуві копії
![]() вправо наτ
або вліво на –τ
відносно початку відліку часового
зсуву τ=0
є парною і симетричною. Приклади побудови
АКФ для одиночного прямокутного
відеоімпульсу і одиночного прямокутного
радіоімпульсу показані на рис.2.33,а,б.
вправо наτ
або вліво на –τ
відносно початку відліку часового
зсуву τ=0
є парною і симетричною. Приклади побудови
АКФ для одиночного прямокутного
відеоімпульсу і одиночного прямокутного
радіоімпульсу показані на рис.2.33,а,б.
Математично АКФ описується виразами:
![]() для
відеоімпульсу,
для
відеоімпульсу,
![]() для
радіоімпульсу.
для
радіоімпульсу.
Таким чином, при τ=0 значення АКФ рівне енергії сигналу на опорі 1Ом. На рис.2.33,в показані також АКФ для пачки з трьох відеоімпульсів прямокутної форми.
Для періодичних детермінованих сигналів кореляційна функція визначається з виразу:
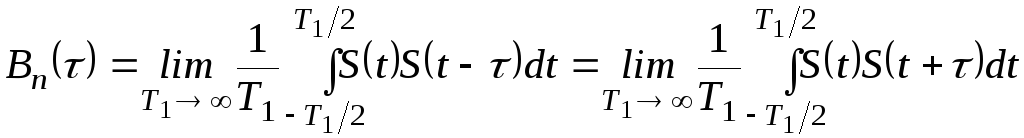 ,
,
де параметр Т1 означає інтервал спостереження сигналу, який для періодичного сигналу може бути рівний його періоду Т. Тоді вираз (2.94) можна записати у вигляді:
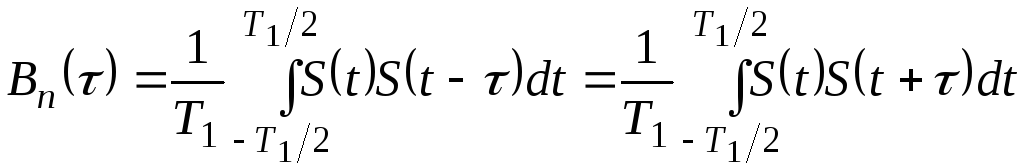 .
(2.95)
.
(2.95)
З виразу (2.95) виходить, що АКФ періодичного сигналу є парною і симетричною, а при τ = 0 її значення рівне потужності сигналу на опорі 1Ом.
Приклади побудови АКФ для деяких видів періодичних сигналів показані на рис.2.34. З рисунку виходить, що АКФ періодичного сигналу є також періодичною функцією з періодом Т.
Математично АКФ на періоді періодичного сигналу описується виразами:
а) для послідовності прямокутних відеоімпульсів:
![]() ,
,
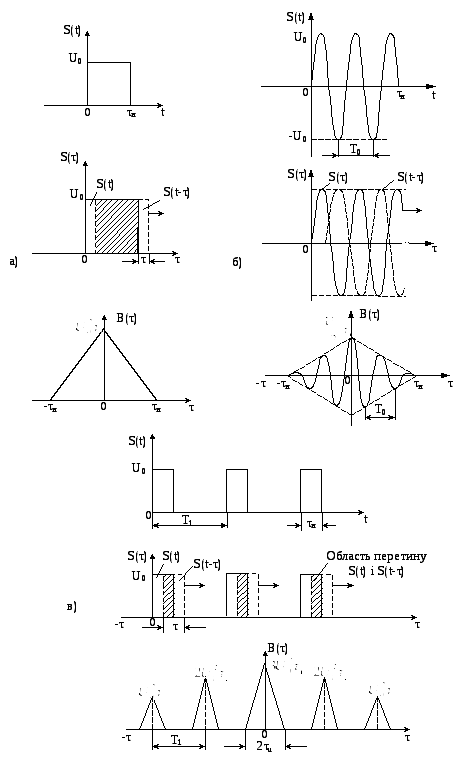
Рисунок 2.33 - Приклади побудови АКФ неперіодичних сигналів
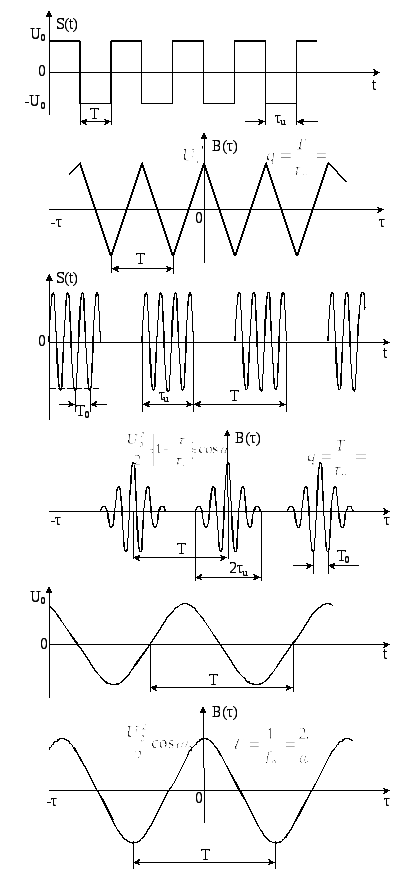
Рисунок 2.34 - Приклади побудови АКФ для деяких видів
періодичних сигналів
б) для послідовності прямокутних радіоімпульсів:
![]() ;
;
в)
для гармонійних сигналів вигляду
![]() або
або![]() :
:
![]() .
.
Функція
кореляції визначає зв'язок між шириною
спектру сигналу і часовим інтервалом
τк,
званим інтервалом кореляції. Під
інтервалом кореляції розуміємо
максимальний зсув
![]() ,
в межах якого АКФ зменшується до нуля
при зсуві копії неперіодичного сигналу
на всю тривалість сигналу вправо або
вліво відносноτ = 0.
,
в межах якого АКФ зменшується до нуля
при зсуві копії неперіодичного сигналу
на всю тривалість сигналу вправо або
вліво відносноτ = 0.
Зв'язок
між кореляційною функцією В(τ)
і енергетичним спектром сигналу![]() ,
описується виразами, аналогічними
перетворенням Фур’є:
,
описується виразами, аналогічними
перетворенням Фур’є:
![]() , (2.96)
, (2.96)
![]() (2.97)
(2.97)
Тоді
справедливе твердження, згідно якому
чим ширше енергетичний спектр
![]() сигналу
сигналу![]() ,
тим менше інтервал кореляціїτк,
тобто тим менше зв'язок сигналу
,
тим менше інтервал кореляціїτк,
тобто тим менше зв'язок сигналу
![]() із зсунутою відносно його копією
із зсунутою відносно його копією![]() .
.
Відповідно,
чим більше інтервал кореляції τк,
тим менше ширина енергетичного спектру
![]() сигналу, тобто тим сильніше зв'язок
(кореляція) між сигналом
сигналу, тобто тим сильніше зв'язок
(кореляція) між сигналом![]() і його копією
і його копією![]() .
З виразів (2.96) і (2.97) виходить, що АКФ не
залежить від ФЧХ сигналу
.
З виразів (2.96) і (2.97) виходить, що АКФ не
залежить від ФЧХ сигналу![]() ,
отже, різним по формі сигналам, що мають
однакові амплітудні спектри, відповідають
однакові кореляційні функції.
,
отже, різним по формі сигналам, що мають
однакові амплітудні спектри, відповідають
однакові кореляційні функції.
