5.2 Основні поняття теорії інформації

5.2.1 Часткова кількість інформації

Припустимо що дискретне джерело повідомлень, описане в п. 5.1, видає деяку послідовність символів а. Дамо формальне визначення часткової кількості інформації i(a), що міститься в цьому повідомленні, виходячи з наступних вимог.

1 Кількість інформації i(a) повинна бути аддитивною функцією, тобто для пари взаємно незалежних повідомлень а₁, а₂ воно повинне дорівнювати сумі кількості інформації в кожному з них, тобто i(а₁, а₂)=i(а₁)+ i(а₂).

2 Кількість інформації, що міститься в достовірному повідомленні (що має вірогідність Р(а)=1), дорівнює нулю.

3 Кількість інформації повинна залежити тільки від вірогідності переданого повідомлення, а не від його змісту, тобто i(a)=f(P(a)).

4 Кількість інформації повинна бути безперервною функцією від Р(а).

5 Кількість інформації є величина невід’ємна, тобто .

Можна показати, що єдина функція, що задовольняє всім цим умовам, має вигляд [50]

. (5.4)

Основа логарифма с в (5.4) може бути вибрана довільною, що впливає лише на одиницю вимірювання кількості інформації.

Якщо с=2, то інформація вимірюється в двійкових одиницях або в бітах, якщо с=е (як в натуральних логарифмах), то інформація вимірюється в натуральних одиницях або в натах, а якщо с=10 (як в десятичних одиницях),то інформація вимірюється в дитах. (Надалі ми побачимо, що вибір основи логарифма ніяк не вплине на основні результати теорії інформації, а саме на теореми кодування.)

Із співвідношення (5.4) видно, що кількість інформації, що міститься в повідомленні, тим більше, чим менше вірогідність його появи, причому кількість інформації, що міститься в повідомленні про «неможливу» подію, рівна нескінченності.

в теорії інформації, що відноситься до зв'язних проблем, не розглядається питання про корисність інформації. Ми завжди виступаємо тут в ролі зв'язківців — «службовців», завдання яких передати по каналах зв'язку видану нам джерелом інформацію, не міркуючи про її корисність.

5.2.2 Ентропія джерела повідомлень

Вище визначено часткову кількість інформації, що міститься в деякій послідовності а, виданою джерелом повідомлень. Проте сам факт генерування саме цієї послідовності є випадковою подією, що має вірогідність Р(а), а, отже, випадковою величиною виявляється і кількість інформації i(a). Тому можна поставити питання про середню кількість інформації, що видається деяким джерелом повідомлень, яке можна визначити як математичне очікування випадкової величини i(a).

Якщо поки обмежитися лише послідовностями довжини п, позначивши їх , то відповідно до відомої формули для математичного очікування дискретної випадкової величини, ми отримуємо

, (5.5)

де підсумовування, як видно, проводиться по всім можливим послідовностям довжини п з елементами, узятими з алфавіту об'єму К. Для того, щоб отримати вичерпну інформаційну характеристику джерела повідомлень, яке, взагалі кажучи, може видавати послідовності необмеженої довжини, потрібно обчислити границю середньої кількості інформації , віднесену до одного символу послідовності.

Отримана величина Н(А), по Шеннону, називається ентропією джерела повідомлень і знаходиться з виразу:

. (5.6)

Якщо береться логарифм по основі 2, то Н(А) вимірюється в бітах на символ повідомлення. Вираз (5.6), очевидно, матиме сенс лише тоді, коли границя в його правій частині існує. Ця властивість виконується для стаціонарних джерел.

Відмітимо, що буква А в позначенні ентропії Н(А) указує на певне джерело з алфавітом А, причому скорочено опускається вид імовірнісного розподілу р(а).

Якщо джерело повідомлень не володіє пам'яттю, то, використовуючи властивість логарифмічної функції, легко показати, що його ентропія буде дорівнювати

, (5.7)

де _{i = 0, 1, …, К-1} – вірогідності видачі джерелом символів повідомлень , причому вони не залежать від номера елементу послідовності, оскільки джерело є стаціонарним.

Визначимо основні властивості ентропії.

1 , причому Н(А)=0 тоді і тільки тоді, коли одна з послідовностей має одиничну вірогідність, а всі інші – нульову. (Ця властивість очевидна з визначення ентропії.)

2 Для будь-якого стаціонарного джерела повідомлень

. (5.8)

Оскільки вираз в правій частині (5.8) – це ентропія джерела без пам'яті, то дана властивість означає, що пам'ять зменшує ентропію джерела.

3 Для будь-якого стаціонарного джерела повідомлень справедлива нерівність

, (5.9)

причому рівність має місце тоді, і лише тоді, коли джерело не має пам'яті і всі його символи рівноімовірні.

З властивості 2 витікає, що при доказі нерівностей (5.9) можливо обмежитися джерелами без пам'яті. Для доказу властивості 3 розглянемо різницю

(5.10)

Далі скористаємося відомою нерівністю .

Тоді маємо

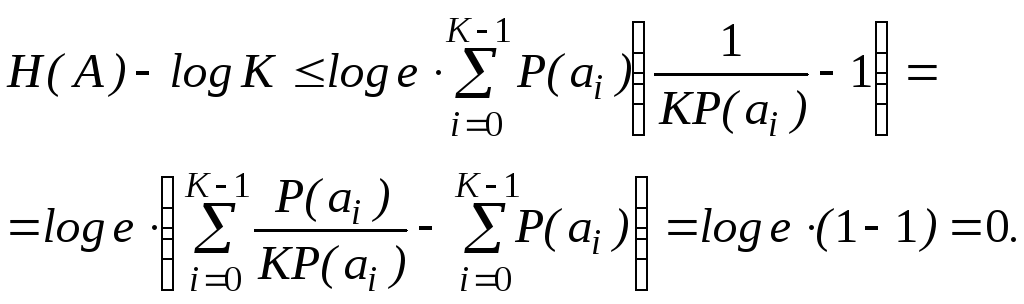(5.11)

Рівність в (5.11) матиме місце тільки при , що і доводить дану властивість.

Скориставшись властивостями 1–3, можна наочно пояснити сенс поняття ентропії – це середня інформативність джерела на один символ, що визначає «несподіванку» або «непередбачуваність» видаваних ним повідомлень. Повністю детерміноване джерело, що видає лише одну, наперед відому послідовність, володіє нульовою інформативністю. Навпаки, найбільш «хаотичне» джерело, що видає взаємно незалежні і рівноімовірні символи, володіє максимальною інформативністю.

Ентропія джерела повідомлень тісно пов'язана з поняттям його надмірності, яке формально визначається таким чином:

(5.12)

Як видно з виразу (5.12), чим більше ентропія джерела, тим менше його надмірність і навпаки.

Відомо, що надмірність природних мов є вельми важливою властивістю, що дозволяє сприймати рукописний або спотворений текст, чути мову у великих акустичних перешкодах і т.п.

Теорія інформації, як ми переконаємося надалі, дозволяє кількісно оцінити ці можливості. Для експериментального обчислення ентропії або надмірності природних мов використовуються статистичні дані про частість, з якою зустрічаються букви тексту і їх поєднання (біграмми, тріграмми і т.п.).

Так, якщо скористатися так званою статистикою англійської мови 1-го порядку (т.е. частістю окремих букв), то ентропія виявляється рівною 4,03 біт/букву, а якщо статистикою порядку, то 3,32 біт/букву. В той же час точнішу оцінку ентропії можна отримати, скориставшись, наприклад, запропонованим ще К. Шенноном «методом випадкового вгадування» [30].

Такий підхід дає верхню оцінку ентропії англійської мови 2 біт/букву і нижню 1 біт/букву. Це дозволяє зробити висновок, що основна надмірність природної мови визначається багатовимірними залежностями між буквами (кореляцією тексту), і для її використання необхідно знати ці залежності.

Аналогічні висновки можна зробити і щодо російського і інших мов, хоча їх ентропії і декілька відрізняються один від одного.

Найбільш просту форму приймає ентропія у разі двійкового джерела повідомлень без пам'яті. Якщо скорочено позначити P(a₀)=P(0) і P(a₁)=P(1), то

(5.13)

Вид цієї функції показаний на рисунку 5.1 для основи логарифма, рівної двом.

Якщо джерело повідомлень має фіксовану швидкість, симв/с, то визначимо продуктивність джерела як ентропію в одиницю часу, (секунду):

(5.14)

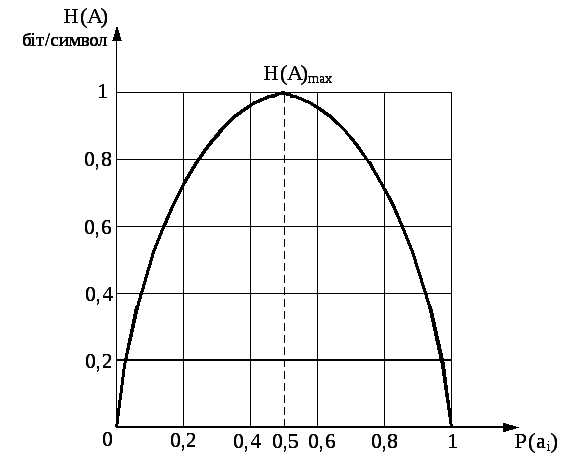
Рисунок 5.1 – Ентропія двійкового джерела без пам'яті

Максимум вираза (5.14), що дорівнює (біт/с) зазвичай називають інформаційною швидкістю джерела повідомлень.