5.2. Интегрирование по частям
Т.5.2. (интегрирование по частям в определенном интеграле)
Если функции u = u(x) и v = v(x) имеют непрерывные производные на отрезке [a;b], то справедлива формула интегрирования по частям в определенном интеграле:
.
Пример. Вычислить
интеграл
Решение
Вопрос 6. Несобственные интегралы
При введении определенного интеграла как предела интегральной суммы мы исходили из условий ограниченности подынтегральной функции и конечности пределов интегрирования.
О.6.1.Определенный
интеграл
где промежуток интегрирования [a;b]
конечен, а подынтегральная функция f(x)
непрерывна (ограничена) на отрезке
[a;b], называется
собственным интегралом. Если хотя
бы одно из двух выше указанных условий
нарушается, то интеграл называется
несобственным.
6.1.Несобственные интегралы с бесконечными пределами интегрирования (несобственные интегралы I-го рода)
Пусть функция y = f(x) непрерывна на полуинтервале [a;+).
О.6.2.Несобственным
интегралом I-го рода от функции
f(x) на
промежутке [a;+)
называется предел интеграла
при b+:
.
(7)
Если предел (7) существует и конечен, то несобственный интеграл
(8)
называется сходящимся. Если предел (7) не существует или бесконечен, то интеграл (8) называется расходящимся.
Аналогично определяется несобственный интеграл от функции f(x) на промежутке (‒;b]:
.
Несобственный интеграл с двумя бесконечными пределами определяется формулой
,
где с – произвольное число. В этом случае интеграл слева сходится тогда и только тогда, когда сходятся оба интеграла справа.
Пример. Вычислить несобственные интегралы или установить их расходимость.
интеграл сходится.
- предел не существует
интеграл расходится.
Замечание
Если F(x)
- первообразная для функции f(x),
то по основной формуле интегрирования
можно записать:
6.2. Несобственные интеграла от неограниченных функций (несобственные интегралы II-го рода)
Пусть функция y = f(x) определена на промежутке [a;b).
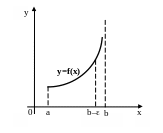
О.6.3. Точка x = b называется особой точкой для функции f(x), если f(x) не ограничена в любой окрестности этой точки, но ограничена на любом отрезке, заключенном в полуинтервале [a;b).
Пусть функция y = f(x) не ограничена в окрестности точки b (т.е. в точке x = b имеет бесконечный разрыв), но при любом достаточно малом > 0 является ограниченной и интегрируемой на отрезке
[a;b ‒ ].
О.6.4.
Несобственным интегралом II-го рода
от функции f(x)
по отрезку [a;b],
где x = b -
особая точка, называется предел интеграла
при 0+0:
.
(9)
Если предел (9) существует и конечен, то несобственный интеграл
(10)
называется сходящимся. Если предел (9) не существует или бесконечен, то интеграл (10) называется расходящимся.
Аналогично, если x = a - особая точка, то несобственный интеграл II-го рода определяется так:
.
Если x = c - особая точка и c(a;b), то несобственный интеграл II-го рода определяется формулой
.
(11)
Интеграл слева в формуле (11) сходится тогда и только тогда, когда сходятся оба несобственных интеграла, стоящих справа.
Если x = a и x = b - особые точки, то несобственный интеграл II-го рода так же определяется формулой (11), в которой с – любая точка из интервала (a;b).
Замечание. Особых точек может быть конечное число.
Пример. Вычислить несобственные интегралы или установить их расходимость.
интеграл сходится.
интеграл
расходится.