1.3 Параметры импульсов и импульсных последовательностей

Рассмотрим передачу информации импульсными сигналами. Для импульсов прямоугольной формы постоянная составляющая X₀=X_mt_и/T₀ а амплитуда n-й гармоники выражается формулой

. (1.7)

Отдельные составляющие спектра отстоят друг от друга на частоту импульсов, т. е. в спектре содержатся только частоты f₀, 2f₀, Зf₀ и т. д. Амплитуды гармоник пропорциональны амплитуде импульсов, но на частотах, где аргумент синуса равен k(k - целое число). А на частотах nf₀ = 1/t_и, 2/t_и, 3/t_и, ..., они обращаются в нуль.

При уменьшении частоты импульсов интервалы между отдельными гармониками сокращаются. Положение же нулевых амплитуд остается неизменным, поскольку оно определяется только длительностью импульсов. Следовательно, уменьшение частоты f₀ ведет к обогащению спектра гармониками, спектр становится гуще. Амплитуда каждой гармоники и постоянная составляющая при этом уменьшаются.

При увеличении периода импульсов до бесконечности интервалы между гармониками стремятся к нулю. Число гармоник стремится к бесконечности, спектр становится сплошным, как это показано на рис. 1.3,г.

При увеличении частоты импульсов f интервалы между гармониками возрастают, спектр обедняется гармониками. При уменьшении длительности импульсов нулевые амплитуды спектра отодвигаются вправо, в сторону больших частот. Положение гармоник на частотной оси при этом не меняется. Следовательно, число гармоник с амплитудами, превышающими некоторый определенный уровень, возрастает, т. е. спектр колебаний расширяется. Чем уже импульс, тем шире его спектр, и наоборот.

Суммарная энергия всех колебаний, составляющих спектр импульса, равна энергии, сосредоточенной в импульсе. Зависимость относительной энергии W колебаний ограниченной полосы частот для импульсов разных типов приведена на рис. 1.7. Видно, например, что для прямоугольного импульса (кривая 1) в полосе частот 0 < f< 2/t_и заключено примерно 95 % всей энергии импульса, а на остальную часть спектра приходится только 5 % энергии. Большей сосредоточенностью энергии в спектре обладают импульсы треугольной формы (кривая 2) и колокольной формы (кривая 3). Отсюда следует, что электронное устройство, предназначенное для воспроизведения периодической последовательности импульсов, должно без искажений передавать частоты от f до (1-2)/t_и. Например, при f =1 кГц и t_u=1 мкс полоса воспроизводимых частот простирается от 1 кГц до 1-2 МГц. Для одиночных импульсов нижняя граница полосы пропускания доходит вплоть до нуля.

При постепенном уменьшении длительноcти импульса, но сохранении его площади (равной единице) спектр импульса непрерывно расширяется и в пределе, когда импульс описывается δ-функцией, t_и стремится к нулю, а амплитуда Х_т - к бесконечности, спектр становится равномерным и простирается в бесконечность.

Когда, например, требуется определить частотную характеристику электронной схемы, то удобно использовать воздействие, описываемое δ - функцией. Благодаря равномерности спектра δ -функции спектр выходного сигнала повторит частотную характеристику устройства. Возможен и другой подход к оценке временных параметров сигналов и воздействий, основанный на оценке их формы кривой. Чаще всего речь идет об импульсах, которые по форме близки к простым геометрическим фигурам (рис. 1.8).Различают импульсы: прямоугольные (а); трапецеидальные (б); треугольные (в); пилообразные (г); экспоненциальные (д); колоколообразные (е). У реального импульса переходы между его отдельными участками плавные, что не позволяет четко фиксировать длительность участков. Поэтому прибегают к понятию активной длительности, которым пользуются в экспериментах и при учете реальной формы импульсов (рис. 1.9).

Активной длительностью прямоугольного импульсаt_и называют промежуток времени между началом нарастания и окончанием спада импульса, отсчитанными по уровню 0,1Х_m, где Х_т - амплитуда импульса. Активная длительность нарастания импульса t_ф и спада его t_c определяется интервалом времени между моментами, в которые высота импульса принимает значения 0,9Х_т и 0,1Х_т. Время задержки импульса t_зд- время от момента, когда высота импульса равна нулю, до момента, когда она станет равной 0,1Х_m . Степень негоризонтальности вершины (длительность последней равна t_и - t_ф- t_c) характеризуется сколом (неравномерностью). Скол Х_m определяется как разность амплитуды импульса и высоты его в начале спада. После спада импульса часто образуется обратный выброс с полярностью, противоположной полярности основного импульса, амплитудой Х_в и длительностью t_в. Это так называемый хвост импульса. Хвост может быть как апериодического, так и колебательного характера. Время t_в называют временем восстановления. В большом числе практических случаев нарастание импульсов носит экспоненциальный характер (рис. 1.9) и описывается уравнением х = Х_m [1 - ехр (-t/τ)]. Спад импульса описывается уравнением экспоненты х= Х_т ехр (-t/τ), где τ - постоянная времени экспоненты. Значения активной длительности импульса находят после решения этих уравнений относительно t:

(1-8)

Подставляя сюда значения х = 0,1Х_т и 0,9Х_m, найдем время нарастания t_ф=t(0,9Х_m) - t(0,lX_m) 2,2τ и время спада t_c  2,2τ.

Для управления цифровыми устройствами часто используются перепады напряжения, которые представляют собой скачкообразные изменения напряжения между двумя уровнями. Перепад от низкого уровня к высокому называют положительным и, наоборот, если напряжение изменяется от высокого уровня к низкому - отрицательным.

Вимпульсной технике часто приходится иметь дело с последовательностями импульсов, которые периодически повторяются через промежуток времениТ, который называют периодом следования (рис. 1.10). Интервал времени между импульсами называется длительностью паузы t_п. Последовательность импульсов характеризуется также частотой повторения f = 1/T, скважностью Q = T/t_и и коэффициентом заполнения k₃ = t_и/T = 1/Q. Дополнительными параметрами для последовательности импульсов являются также среднее значение напряжения или тока за период Т:

и действующее значение

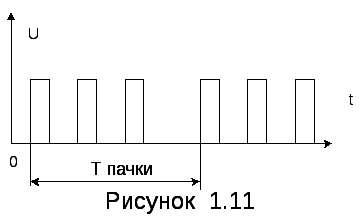
Для последовательности прямоугольных импульсов U_cp = U_m/Q, U_Д=U_m/Q, т.е. - действующее значение U_Д напряжения последовательности прямоугольных импульсов больше среднего значения в раз. Кроме последовательностей одиночных импульсов в цифровой технике широко используются также последовательности пачек импульсов (рис. 1.11), каждая из которых состоит из нескольких импульсов. Длительность паузы между импульсами в одной пачке иногда бывает переменной и является важным параметром импульсного сигнала, образуемого пачкой импульсов.

Ч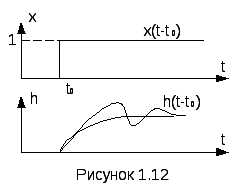тобы судить о возможностяхформирования, передачи и приема сигналов и воздействий с помощью той или иной аппаратуры, прибегают к исследованию ее переходных характеристик. Переходная характеристика представляет собой зависимость выходного параметра (тока, напряжения) от времени при скачкообразном входном воздействии. Такое воздействие дает возможность выяснить реакцию устройства сразу в двух режимах: при мгновенном изменении входного сигнала (переходный режим) и при постоянном его значении (статический режим). Иначе говоря, переходная функция h(t-t₀) находится как нормальная реакция системы (т. е. реакция при нулевых начальных условиях) на воздействие в виде единичной ступенчатой функции (рисунок 1.12)

или, что тоже самое, (1.9)

Напомним, что -функция или импульсная функция может быть найдена из единичной ступенчатой путем дифференцирования: (t) = d1(t)/dt.

Нормальную реакцию (t) на импульсное воздействие называют импульсной переходной функцией. Нормальная реакция устройства на произвольное воздействие х(t) выражается через импульсную переходную функцию с помощью интеграла.

(1.10)

где (τ) играет роль весовой функции.

Очевидно, что реальные входные сигналы имеют меньшую крутизну нарастания и спада, чем переходная характеристика, и ограниченную длительность вершины.

Контрольные вопросы

1. Какие сигналы называются детерминированными и случайными?

2. Какими параметрами характеризуются электрические сигналы?

3. Что такое активная длительность импульса?

4. Как определяются длительность фронта и среза импульса?

5. Что такое спад вершины импульса?

7. Что такое коэффициент заполнения?

11. Какими параметрами импульсов и импульсных последовательностей передаваться информация?

12. Какими параметрами гармонических сигналов может передаваться реформация?

13. Для чего применяют модуляцию?

14. Какие физические носители информации применяют в автоматике?

15 . Что понимают под воздействием, и какие воздействия применяют в электронных элементах автоматике?

16. Выберете тип модуляции для передачи информации от датчиков по силовому кабелю электробура глубинной скважины.

17. С какой частотой необходимо производить дискретизацию?

18. Определите, какая часть спектра сигнала связана с искажениями фронта и плоской вершины импульса.

19. Как будет изменяться спектр сигнала, если длительность прямоугольного импульса будет приближаться к длительности паузы?

20. Какой сигнал обладает самым узким и самым широким спектром?