
- •Министерство образования и науки украины
- •В. Л. Лисицкий автоматизация операционных исследований на базе персональных эвм
- •7080401 – Информационные управляющие системы и технологии; 7080403 – Программное обеспечение автоматизированных систем.
- •1 Основные определения. Типовые содержательные задачи линейного программирования, являющиеся задачами исследования операций
- •1.1. Основные определения
- •1.2. Типовые содержательные задачи лп, являющиеся задачами исследования операций
- •2 Автоматизация операционных исследований. Структура интерфейса исследователя операций
- •3 Алгоритмическое обеспечение решения задач лп конечными методами
- •4 Программное обеспечениеисследования операций
- •4.1. Основные этапы обработки информации при моделировании операцій
- •4.2. Структура прикладного программного обеспечения исследования операций
- •Для задачи лп
- •4.3. Построение схемы программы
- •4.4. Отладка программы
- •4.5. Описание программы. Описание программы позволяет не только эксплуатировать ее, но и проводить необходимую модернизацию с целью дальнейшего использования в разработках.
- •Контрольные вопросы
- •Список литературы
- •Лисицький Василь Лаврентійович
4.2. Структура прикладного программного обеспечения исследования операций
4.2.1. Состав программного обеспечения. Под прикладным программным обеспечением исследования операции следует понимать комплекс программ, предназначенный для реализации альтернатив главного меню и обеспечения управления обработкой данных на всех этапах процесса имитационного моделирования. Структура прикладного программного обеспечения определяется структурой главного меню, характеризуется наличием конечного числа компонент. Компонент - программа, рассматриваемая как единое целое, выполняющая законченную функцию и применяемая самостоятельно или в составе комплекса. Рассматриваемый комплекс программ может содержать следующие компоненты:
программа, обеспечивающая ввод первичных данных;
программа, обеспечивающая обновление первичных данных;
программа, обеспечивающая решение основной задачи исследования операции;
программа, обеспечивающая проверку достоверности полученного решения;
программа, обеспечивающая исследование устойчивости полученного решения;
программа, обеспечивающая управление обработкой данных на всех этапах имитационного моделирования.
Каждая из указанных программ реализует одну из функций главного меню. В следующих подразделах описаны состав и особенности каждой программы.
4.2.2. Программа
ввода первичных данных. Состав программы
определяется составом подменю 1.1 главного
меню. Программа обеспечивает ввод
первичных данных с ГМД и ввод матрицы
А, векторов![]() с
экрана дисплея, предоставляет возможность
просмотра введенных данных. Требования
к процессу ввода изложены в 4.1.
с
экрана дисплея, предоставляет возможность
просмотра введенных данных. Требования
к процессу ввода изложены в 4.1.
4.2.3. Программа
обновления первичных данных. Состав
программы определяется составом подменю
1.2 главного меню. Программа предоставляет
возможность обновления отдельных
элементов матрицы А, векторов![]() с
экрана дисплея. Требования к процессу
обновления данных изложены в 4.1.
с
экрана дисплея. Требования к процессу
обновления данных изложены в 4.1.
4.2.4. Программа решения основной задачи исследования операций. Состав программы определяется составом подменю 1.3 главного меню. Программа обеспечивает построение канонической формы (3.1) записи задачи ЛП, построения (в случае вариантов 11, III, 1V) вспомогательной задачи заданным конечным методом, вывод результатов решения на экран или принтер. В разделе 3 описано алгоритмическое обеспечение решения задач ЛП конечными методами. В соответствии с последовательностью обработки данных, задаваемой общей схемой метода, подпрограмма решения задачи ЛП может быть структурирована на уровне текстовых модулей и содержать:
а) программу формирования исходных таблиц;
б) программу просмотра исходных таблиц;
в) программу определения наличия ситуации 1;
г) программу определения наличия ситуации 2;
д) программы определения номеров направляющего столбца и направляющей строки таблицы;
е) программы определения параметров новой таблицы;
ж) программу контроля достоверности промежуточных вычислений.
Необходимость
контроля обусловлена накоплением ошибок
округления из-за ограниченности разрядной
сетки ПЭВМ. Если эти ошибки достигают
заданной величины, то применяют программы
обновления таблиц, соответствующих
рассматриваемому на данной итерации
базису текущего опорного плана. Контроль
осуществляют периодически через p=[m/3]
итераций, гдеm-
число ограничений,[ ] - целая часть
числаm/3. Промежуточный
контроль достоверности вычислений
основан на сравнении величин, которые
могут определяться различными способами.
В первом алгоритме, такими величинами
являются параметры![]() , во втором алгоритме - параметры
, во втором алгоритме - параметры![]() .
.
Контроль
достоверности вычислений
![]() .Параметры
.Параметры
![]() для вновь полученного базиса могут быть
вычислены двумя способами:
для вновь полученного базиса могут быть
вычислены двумя способами:
по формулам (3.4)

-по формулам (3.3)
![]()
Сравнение
![]() и
и
![]() осуществляется
с помощью
осуществляется
с помощью
![]()
Контроль
достоверности вычислений
![]() .Параметры
.Параметры
![]() для вновь получаемого базиса
для вновь получаемого базиса
![]() могут быть вычислены двумя способами:
могут быть вычислены двумя способами:
по рекуррентным формулам
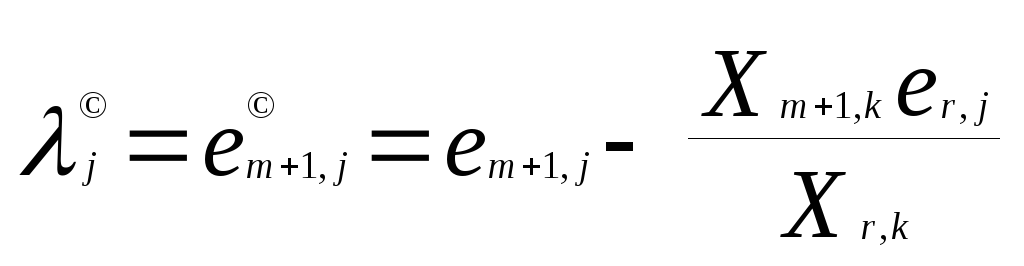
по формулам (3.6)
![]()
Сравнение
![]() и
и
![]() осуществляется
с погрешностью
осуществляется
с погрешностью
![]()
![]()
Допустимая
погрешность
![]() промежуточных вычислений, как правило,
определяется точностью задания исходных
данных, точностными требованиями к
оптимальному плану основной задачи,
промежуточных вычислений, как правило,
определяется точностью задания исходных
данных, точностными требованиями к
оптимальному плану основной задачи,
з) программу анализа полученного решения;
и) управляющую программу, обеспечивающую передачу управления от одной программы к другой в соответствии с требованиями алгоритма конечного метода.
Требования к процессу решения основной задачи исследования
операции изложены в 4.1.
4.2.5. Программа проверки достоверности решения основной задачи. Состав программы определяется составом подменю 1.4 главного меню, содержит четыре подпрограммы:
а) программа проверки допустимости осуществляет:
в случай первого алгоритмапроверку неотрицательности
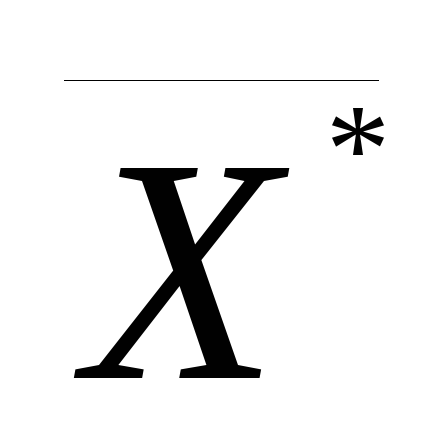 и
выполнения условий
и
выполнения условий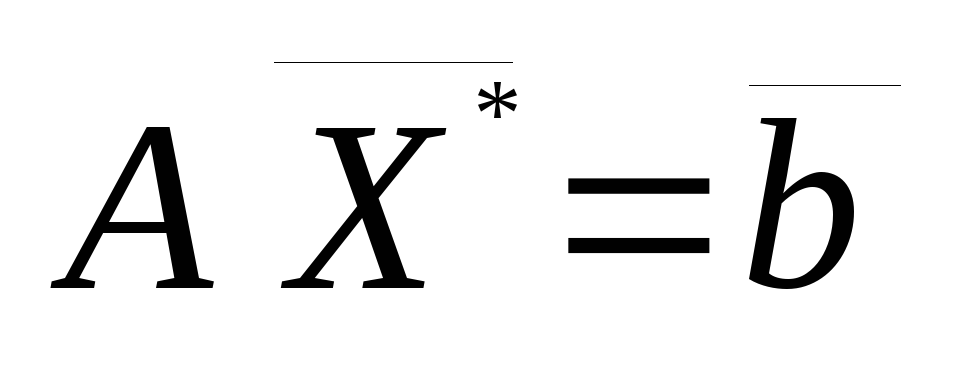 задачи
(3.1);
задачи
(3.1);в случае второго алгоритмапроверку неотрицательности
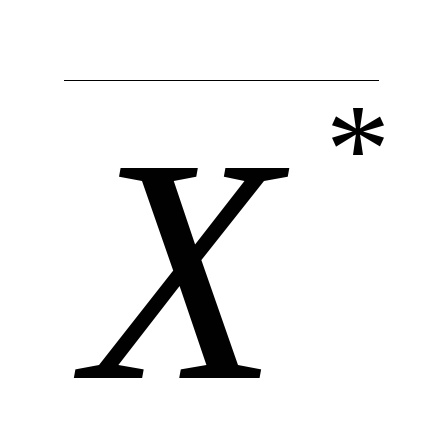 , выполнение ограничений
, выполнение ограничений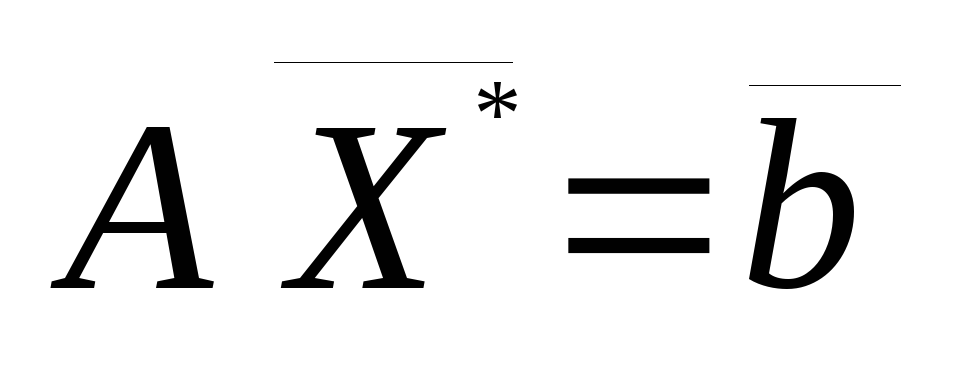 задачи
(3.1), а также выполнения условий
задачи
(3.1), а также выполнения условий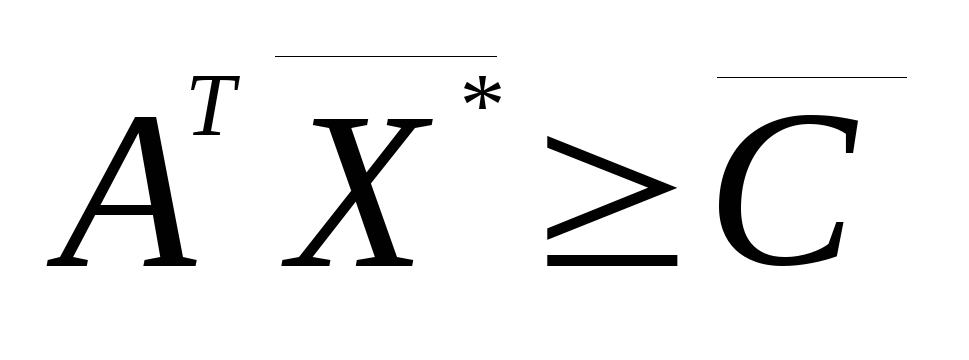 задачи,
двойственной к (3.1), где
задачи,
двойственной к (3.1), где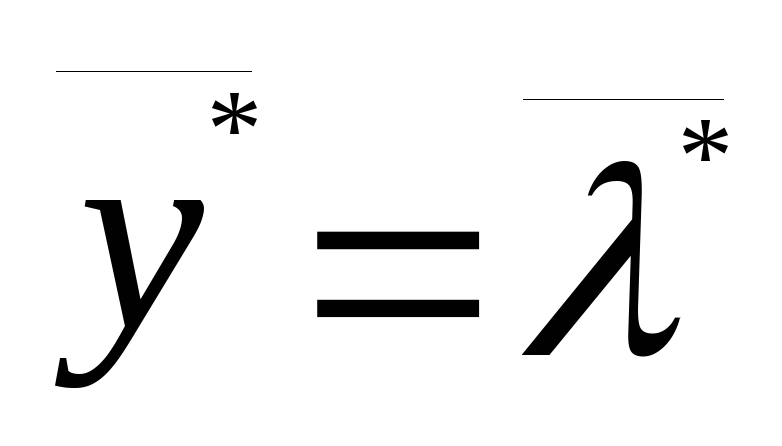
б) программа
проверки опорностиосуществляет
проверку линейной независимости векторов![]() путем вычисления определителя матрицы
путем вычисления определителя матрицы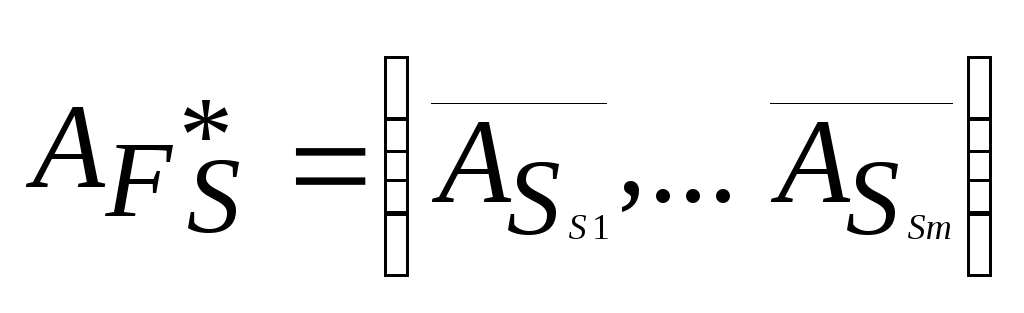 Если
Если![]() ,
то вектора условий, соответствующий
базисным компонентам
,
то вектора условий, соответствующий
базисным компонентам![]() линейно
независимы и задает вершину допустимого
множества задачи (3.1);
линейно
независимы и задает вершину допустимого
множества задачи (3.1);
в) программа
проверки оптимальностиосуществляет проверку равенства значений
прямой![]() и двойственной
и двойственной![]() задач двойственной пары:
задач двойственной пары:
В случае первого
алгоритмавычисляется значение
![]() ,опорный план двойственной задачи
,опорный план двойственной задачи![]() .
Значение
.
Значение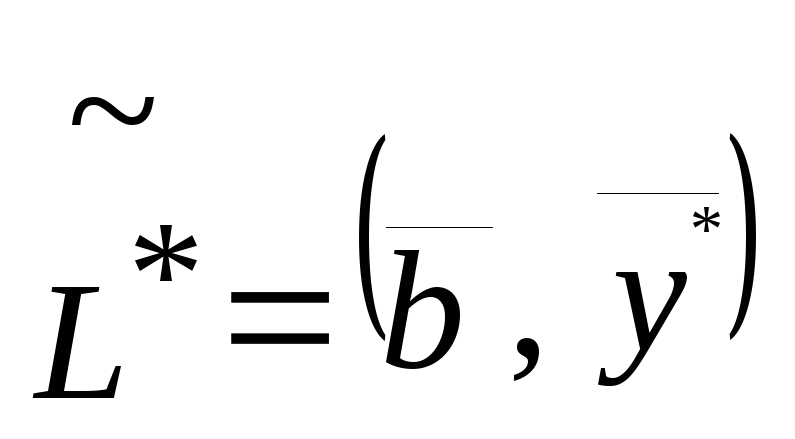 .
Если
.
Если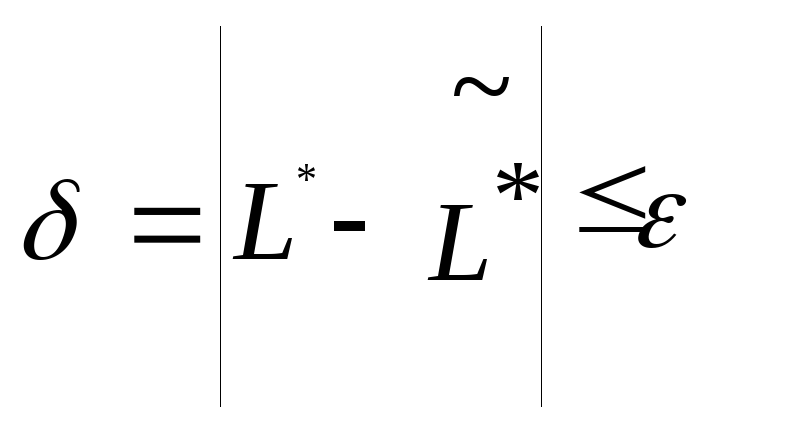 ,
то считается справедливым выполнение
равенства
,
то считается справедливым выполнение
равенства
 и
делается заключение о достоверности
решения
и
делается заключение о достоверности
решения
![]() задачи (3.1), полученного с помощью ПЭВМ,
в случаевторого алгоритмавычисляется
задачи (3.1), полученного с помощью ПЭВМ,
в случаевторого алгоритмавычисляется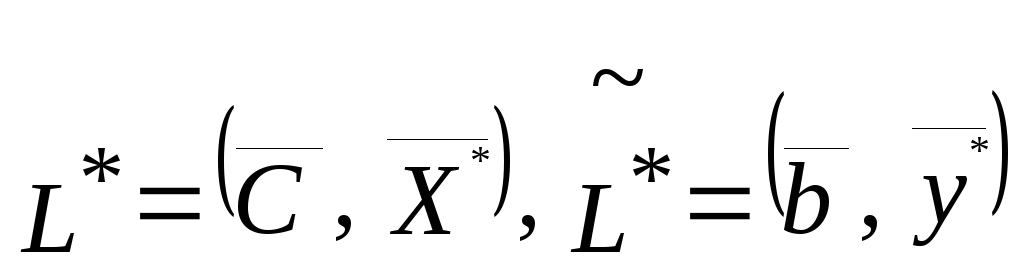 Если
Если
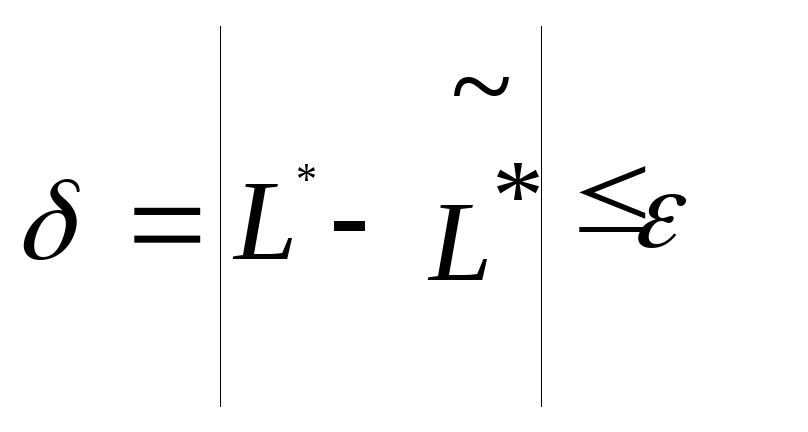 ,
то считается справедливым выполнение
равенства
,
то считается справедливым выполнение
равенства
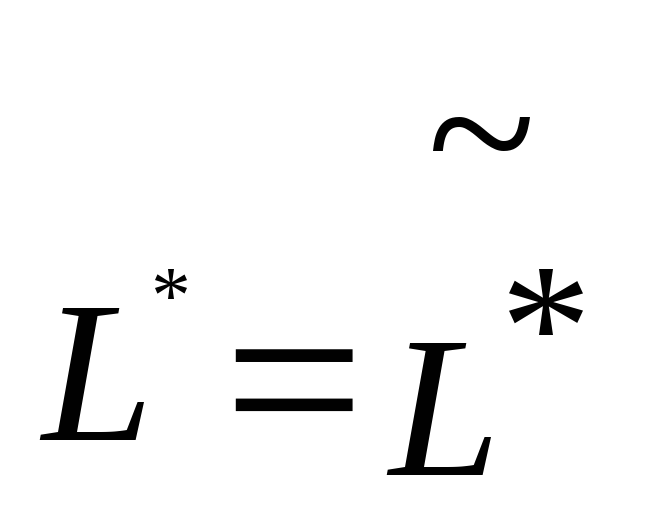 и
делается заключение о достоверности
решений
и
делается заключение о достоверности
решений![]() ,
,![]() '
задач двойственной пары, полученных с
помощью ПЭВМ.
'
задач двойственной пары, полученных с
помощью ПЭВМ.
Если
![]() ,
где
,
где
![]() - допустимая погрешность вычисления
значения задачи (3.1), то полученное
"решение" достаточно "далеко"
от оптимального. Пользователю необходимо
выдать сообщение о полученных результатах
и рекомендации о возможных его действиях.
- допустимая погрешность вычисления
значения задачи (3.1), то полученное
"решение" достаточно "далеко"
от оптимального. Пользователю необходимо
выдать сообщение о полученных результатах
и рекомендации о возможных его действиях.
4.2.6. Программа
исследования устойчивости полученного
решения. Состав программы определяется
составом подменю 1.5 главного меню.
Программа обеспечивает возможность
исследования влияния изменения параметров
задачи на оптимальный базис
![]() ,
изменение значений задачи
,
изменение значений задачи![]() .
.
Для построения
области устойчивости оптимального
базиса при возникновении активных
средств операции используется
аналитическое выражение множества![]()
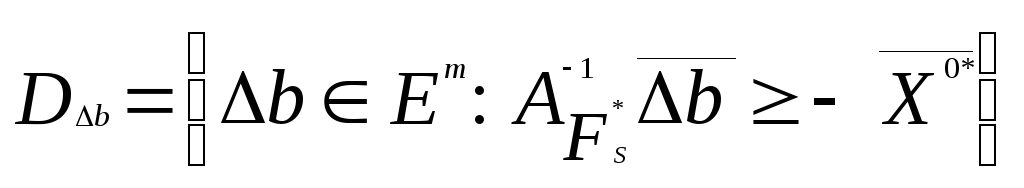
определяющее
множество приращений![]() правых частей задачи (3.1), при которых
правых частей задачи (3.1), при которых![]() сохраняет свойство оптимальности.
сохраняет свойство оптимальности.
![]() m-мерное евклидовое
пространство,
m-мерное евклидовое
пространство,![]() - базисные компоненты оптимального
плана задачи (3.2),
- базисные компоненты оптимального
плана задачи (3.2),![]() - матрица, обратная матрице
- матрица, обратная матрице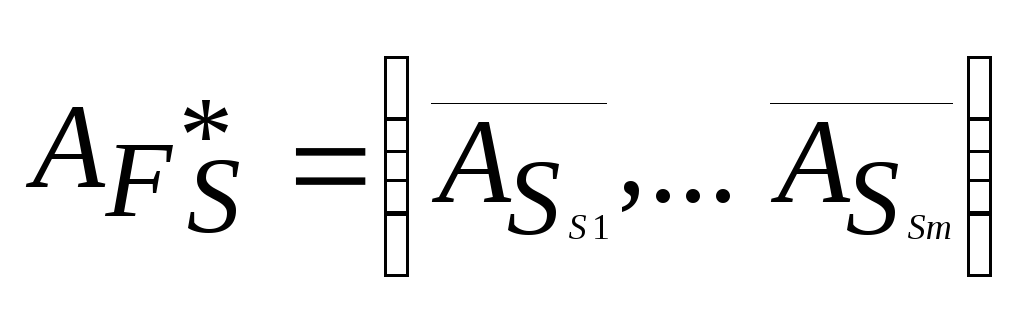 ,
составленной из векторов
условий оптимального базиса
,
составленной из векторов
условий оптимального базиса
![]() .Для получения "сечений" множества
.Для получения "сечений" множества![]() на
экране дисплея, рассматривают случай,
когда
на
экране дисплея, рассматривают случай,
когда![]() .
Номера
.
Номера![]() определяют номера возмущаемых активных
средств системы. В этом случае множество
определяют номера возмущаемых активных
средств системы. В этом случае множество![]() определяется
формулой
определяется
формулой![]()
![]() задает
пределы изменений
задает
пределы изменений![]() -го
и
-го
и![]() -го
активных средств системы, при которых
базис
-го
активных средств системы, при которых
базис
![]() сохраняет
свойство оптимальности.
сохраняет
свойство оптимальности.
Изменение
оптимального базиса соответствует
«структурной» перестройке проведения
операции. Среди возмущений
![]() '
следует выделять допустимые, то есть
такие, при которых система сохраняет
способность достижения цели операции.
Как правило, множество
'
следует выделять допустимые, то есть
такие, при которых система сохраняет
способность достижения цели операции.
Как правило, множество![]() - допустимых изменений
- допустимых изменений![]() задается параллелепипедом
задается параллелепипедом
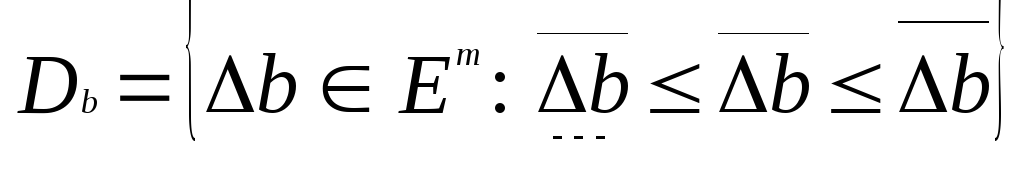
Если в задаче (3.1)
уровень
![]() не
может быть меньше заданного порогового
уровня, то
не
может быть меньше заданного порогового
уровня, то![]() .
Для
.
Для![]() ,
значение
,
значение![]() .
.
Множество
![]() определяет
множество допустимых изменений правых
частей задачи (3.1), при которых
определяет
множество допустимых изменений правых
частей задачи (3.1), при которых
![]() сохраняет свойство оптимальности.
сохраняет свойство оптимальности.
Рассмотрим пример, иллюстрирующий порядок действий при исследовании устойчивости оптимального базиса.
Пример 4.1.
