3 Алгоритмическое обеспечение решения задач лп конечными методами

3.1. Общая схема и классификация конечных методов решения

задач ЛП

Каждый конечный метод предполагает:

- представление задачи ЛП в канонической форме

;

- частичный направленный перебор вершин допустимого множества

};

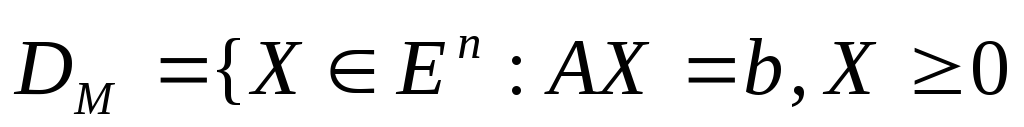задачи ЛП с целью поиска ее оптимального плана

Каждый конечный метод характеризуется тремя основными моментами.

1. Наличие начального опорного плана , определяющего исходную вершину допустимого множества, из которой начинается движение в оптимальную вершину

2. Наличие признака оптимальности, с помощью которого можно проверять оптимальность каждой текущей вершины . Наличие механизма, с помощью которого в случае неоптимальности вершиныможно осуществить переход к новому опорному плану, более близкому к оптимальному (с большим значением целевой функции).На рис. 3.1 представлена общая схема конечного метода

Для разрешимых задач ЛП любой конечный метод позволяет через конечное число итераций указать точное решение задачи.

Все конечные методы делятся на три группы:

А. Метод последовательного улучшения плана (метод А).

В. Метод последовательного уточнения оценок (метод В).

С. Метод последовательного сокращения невязок (метод С).

Методы А и В могут быть реализованы двумя алгоритмами:

A-І (B-І) - первый алгоритм метода A( B )

A-II (B-II)- второй алгоритм метода A( B ).

При реализации обоих алгоритмов метода A начальная вершина , может быть определена различными способами, определяющими различные модификации І и ІІ алгоритмов метода последовательного улучшения плана:

Вариант І - случай наличия единичного базиса в условиях исходной задачи,

Вариант ІІ - случай возможности организации единичного базиса в условиях задачи;

Вариант ІІІ- метод искусственного базиса,

Вариант IV- "М-метод" решения задачи ЛП.

Каждый из указанных вариантов может использовать І или ІІ алгоритм метода А.

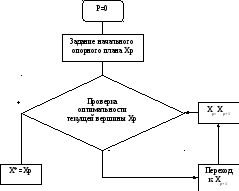
Рис. 3.1 Общая схема конечного метода.

3.2. Метод последовательного улучшения плана (І алгоритм)

При применении данного метода задачу ЛП необходимо представить в канонической форме записи

(3.1)

где - план задачи,- вектор ограничений,- матрица условий размером

- вектор условий, - вектор коэффициентов линейной формы L.

Кроме того, необходимо указать опорный план задачи (3.1) с базисом.Последовательное продвижение по базисам опорных планов задачи (3.1) вплоть до получения оптимального базиса составляет идею метода последовательного улучшения плана.

Первый алгоритм начинается с заполнения таблицы 3.1. для исходного базиса F_s .

В первый столбец таблицы заносят номера позиций базиса, во второй столбец - базисные компоненты C_siвектора.

Столбец F_sсодержит информацию о номерах S_iвекторов условий, принадлежащих F_s. Столбцы A_0,A_1,...,A_n заполняют элементами матрицы X, определяемой по формуле

, (3.2)

где- расширенная матрица условий, X_i0- базисные компоненты опорного плана, X_ij - коэффициенты разложения векторов условийпо базису F_s. Последняя m+1 строка заполняется на основе информации предыдущих строк

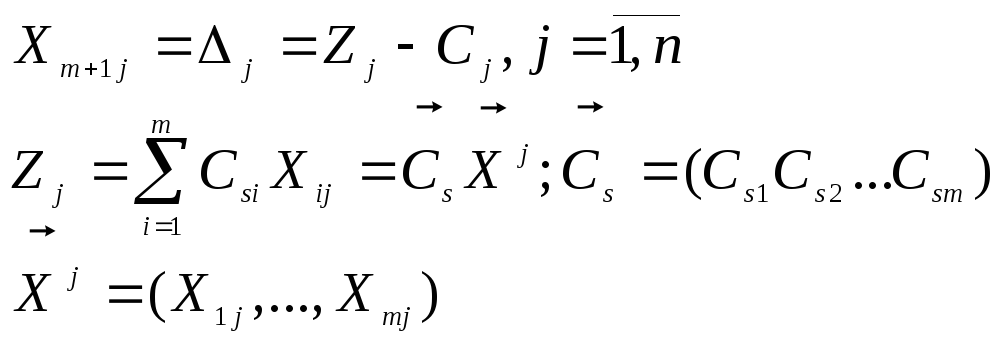(3.3)

Параметр определяет значение целевой функциина опорном плане.Движение в оптимальную вершину

Таблица 3.1 Начальная таблица симплекс-метода

				C1	C2	Cs	...	Ck	...	Cn
№	Cs	Fs	A0	A1	A2	A3	...	Ak	...	An	
1	Cs1	As1	X10	X11	X12	X13	...	X1k	...	X1n
2	Cs2	As2	X20	X21	X22	X23	...	X2k	...	X2n
...	...	...	...	...	...	...	...	...	...	...	...
r	Csr	Asr	Xr0	Xr1	Xr2	Xr3	...	Xrk	...	Xrn	
...	...	...	...	...	...	...	...	...	...	...	...
m	Csm	Asm	Xm0	Xm1	Xm2	Xm3	...	Xmk	...	Xmn
m+1			Z0				...		...

(переход от исходной таблицы к последующей) начинают с установления наличия ситуации 1, для которой выполняются условия . Если срединет строго отрицательных чисел, то исследуемый опорный план является оптимальным и процесс решения задачи прекращается.

Если среди есть отрицательные, то устанавливают существование ситуации 2:для каждого отрицательного параметра. Если существует, то задача (3.1) неразрешима из-за неограниченности линейной формы сверху на множестве планов D_M.

Если ситуация 2 не имеет места, то имеет место ситуация 3, при которой можно перейти в новую вершину D_M, более близкую к оптимальной. Начинается этот переход с определения k - номера направляющего столбца таблицы, задающего номер вектора условий, который должен войти в базис новой вершины. При выборе k можно реализовать два метода.

Точный метод.В качестве направляющего столбца выбирают тот, на котором достигается наибольшее приращениецелевой функции.

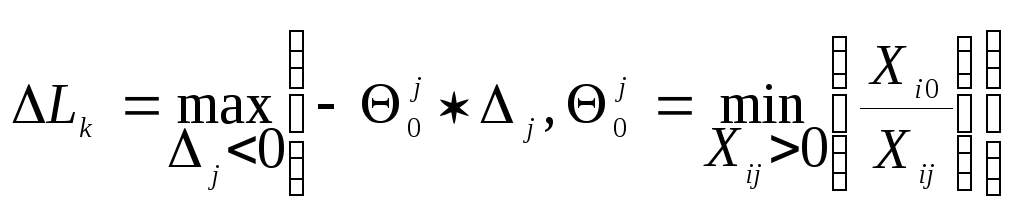
Приближенный метод.В качестве направляющего столбца выбирают тот, на котором достигается наименьшее отрицательное значение.

Для нахождения r - номера направляющей строки, определяющего номер S_rвектора условий, выводимого из базиса F_sпри переходе в новую вершину, вычисляют

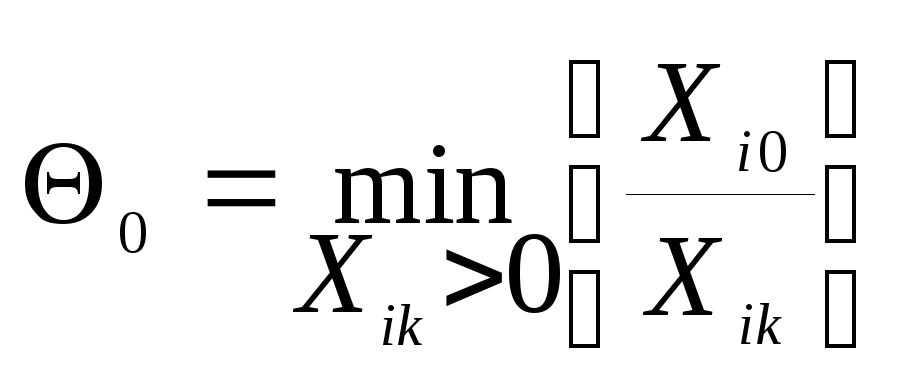
и находят позиции базиса, на которых достигается . Еслидостигается на одной строке таблицы, то она и является направляющей строкой. Если, достигается на нескольких строках таблицы, то в качестве направляющей выбирают ту, которой в столбце F_sсоответствует вектор условий с наименьшим порядковым номером.

После определения номеров k и r формируют базис нового опорного планазаменой в F_sвектора условийна,и формируют новый столбецзаменойна. Остальные элементы столбцов F_sи C_sтаблицы остаются прежними.

Элементы новой матрицы , соответствующей новому опорному плану с базисомпересчитываются по формулам :

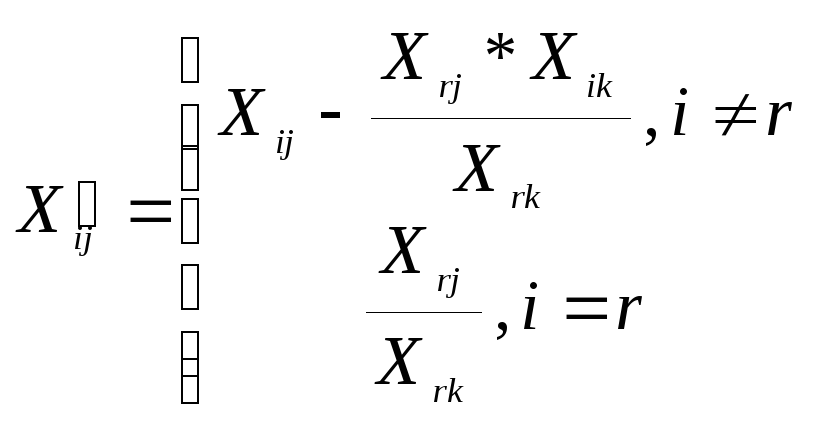(3.4)

где i= 1,2,3,...m+1,j= 0,1,2,...n.

Вновь полученный опорный план берут в качестве начальной вершины, которой соответствует симплекс таблица с элементами. Общая схема метода последовательного улучшения плана (1 алгоритм) приведена на рис. 3.2.

Рассмотрим вычислительный пример, иллюстрирующий порядок действий по первому алгоритму

Пример 3.1.Решить задачу

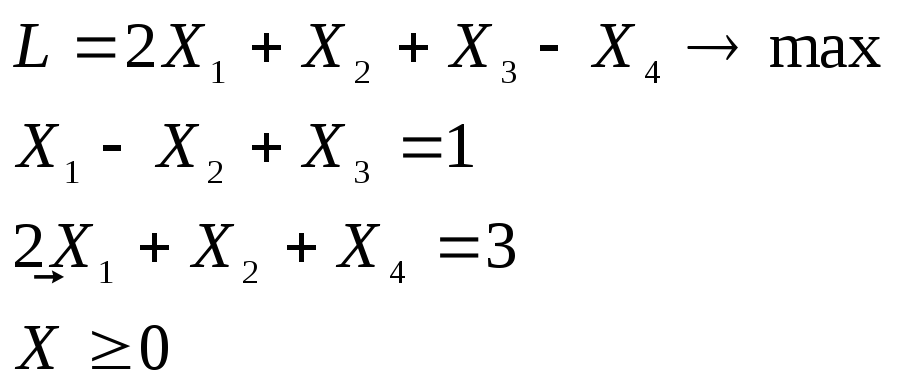
симплекс-методом (первый алгоритм), взяв в качестве исходного опорный план с базисом.

Для заполнения исходной таблицы вычислим матрицу , обратную к. Она имеет элементы. По формуле, находим матрицу коэффициентов разложений векторов условий и вектора ограничений по базису F_s

Параметры определяют по формулам

С учетом выполненных вычислений начальная таблица (табл. 3.2) имеет вид

Движение в оптимальную вершину начинают с анализа ситуаций

Таблица 3.2 Начальная таблица

			C	2	1	1	-1
№	CS	FS	A0	A1	A2	A3	A4	
1	2	A1	1	1	-1	1	0	-----
2	-1	A4	1	0	3	-2	1	1,3
3			1	0	-6	3	0

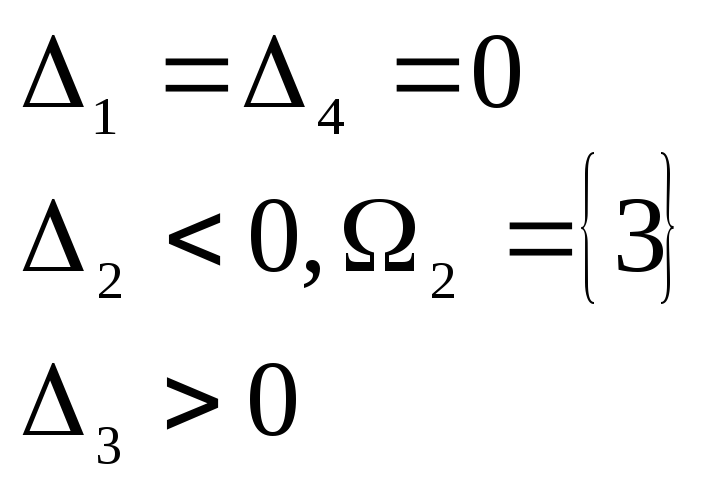
В результате анализа установлена ситуация 3. Номер k однозначно равен 2. , равное 1/3, достигается на второй строке таблицы (r=2). Новый опорный планимеет базис, соответствующая ему таблица пересчитывается по формулам (3.4).

Таблица 3.3 Первая таблица

			C	2	1	1	-1
№	CS	FS	A0	A1	A2	A3	A4	
1	2	A1	4,3	1	0	1,3	1,3	4
2	1	A2	1,3	0	1	-2,3	1,3	-----
3			3	0	0	-1	2

Из анализа ситуаций для таблицы 3.3

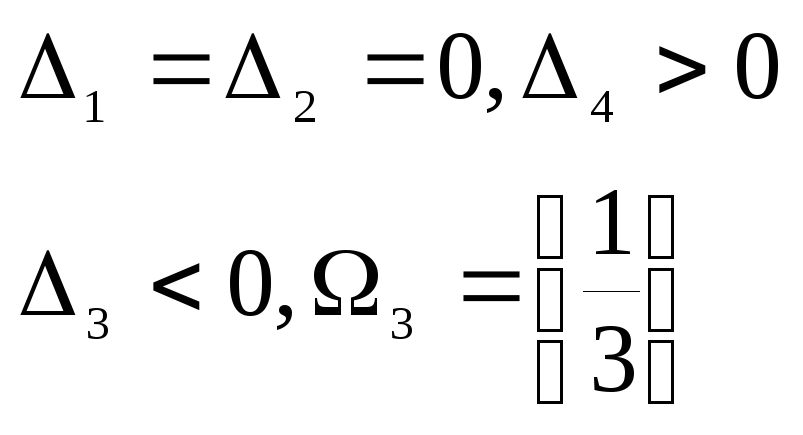
следует наличие ситуации 3. Номер kнаправляющего столбца равен 3 , r=1 , базис нового опорного плана(табл. 3.4)

Из анализа ситуаций для таблицы 3.4

следует, что имеет место ситуация 1.

Таблица 3.4 Конечная таблица

			C	2	1	1	-1
№	CS	FS	A0	A1	A2	A3	A4	
1	1	A3	4	3	1	0	1
2	1	A2	3	2	0	1	-1
3			7	3	0	0	3

Оптимальный базис , оптимальный план, значениезадачи равно 7.

3.3. Метод последовательного улучшения плана (ІІ алгоритм)

Для реализации метода последовательного улучшения плана необходимо, имея начальный опорный план и его базис, уметь на каждом шаге выбирать вектор условий , подлежащий включению в базис, и вектор, подлежащий удалению из базиса. Для перехода от одного опорного плана к другому с большим значением линейной формы необходимо уметь вычислять на каждом шаге базисные компонентыопорного плана и коэффициентыразложения векторапо текущему базису. Возможность получения всех параметров, необходимых для оценки опорного плана и перехода к лучшему с использованием пошагового преобразования обратной матрицыприводит к новой форме реализации процедуры симплекс-метода. В литературе этот метод обычно называют методом обратной матрицы. Для решения задач ЛП рассматриваемым методом ее необходимо представить в канонической форме (3.1) и задать начальный опорный планс базисом. Если в первом алгоритме параметрывычисляют по формуле

(3.5)

то основой второго алгоритма являются другие формулы

(3.6)

где - матрица, составленная из векторов условий, входящих в.

Второй алгоритм симплекс-метода решения задачи (3.1) начинается с заполнения вспомогательной (табл. 3.5) и основной (табл. 3.6) таблиц. Вспомогательная таблица содержит информацию о задаче (3.1) и имеет вид

Таблица З.5  Вспомогательная таблица

№	b	A1	A2	...	Ak	...	An
1	b1	a11	a12	...	a1k	...	a1n
...	...	...	...	...	...	...	...
m	bm	am1	am2	...	amk	...	amn
m+1	C	C1	C2	...	Ck	...	Cn
m+2				...		...

Основная таблица (табл. 3.6) содержит переменную информацию, определяемую базисами опорных планов задачи, перебираемых в процессе движения к оптимальному плану , и имеет вид Здесь e_ij , i,j=1,2,3,...,m - элементы обратной матрицы,

- базисные компоненты опорного плана .

Параметры , при этом

. Движение в оптимальную вершину (переход от исходной таблицы к последующей) начинают с вычисления параметров по формулам (3.6) и установления наличия ситуации 1

Таблица 3.6 Основная таблица

№	CS	FS	E0	e1	...	em	Ak	
1	CS1	AS1	E10	e11	...	e1m	x1k	...
...	...	...	...	...	...	...	...	...
R	CSr	ASr	er0	er1	...	erm	xrk	
...	...	...	...	...	...	...	...	...
M	CSm	ASm	em0	em1	...	emm	x1k	...
m+1					...

. Если среди есть отрицательные, то находят номер направляющего столбца, используя точный или приближенный метод. Зная k, заполняют направляющий столбец A_k, занося в m+1 строку значение, а в остальные строки вектор. Если, то имеет место ситуация 2.

В противном случае находят значение 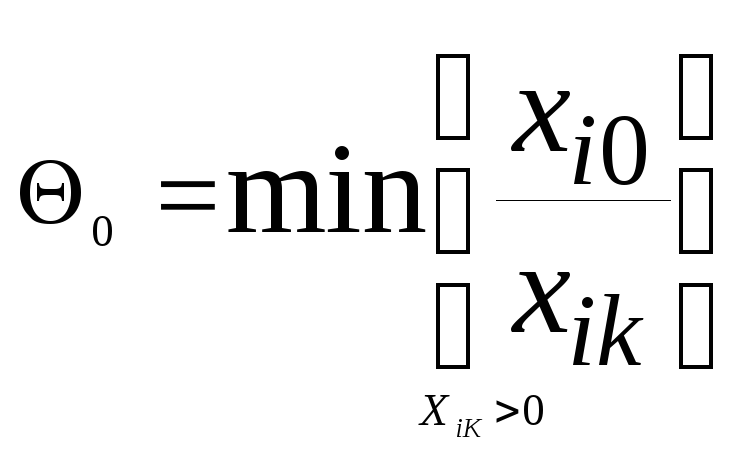и определяют позиции базиса, на которых достигается_.Если_достигается на нескольких строках таблицы, то в качестве направляющей берут ту, в столбце F_sкоторой находится вектор условий с наименьшим порядковым номером.

После определения номеров k и r формируют базис нового опорного планазаменой вектора условийна. Одновременно формируют новый столбец C_Sтаблицы заменой C_Srна C_K. Остальные элементы столбцов F_Sи C_Sостаются прежними.

Элементы: таблицы, соответствующей новому опорному планус базисомпересчитывают по формулам:

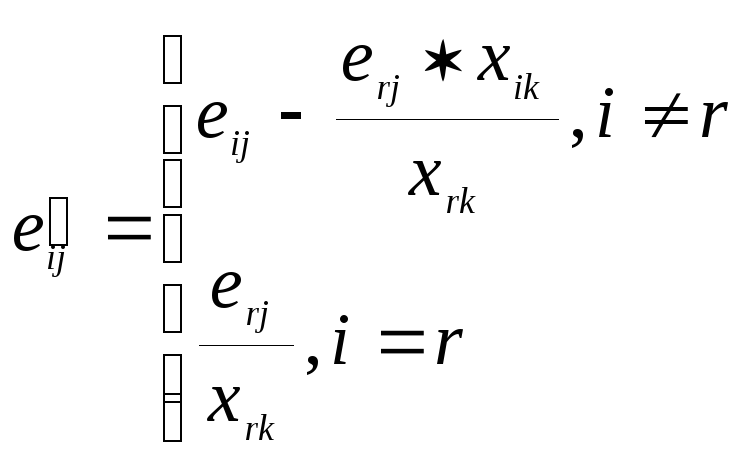
Вновь полученный опорный план берут в качестве исходного, и описанный процесс повторяется. Общая схема метода последовательного улучшения плана (второй алгоритм) приведена на рис. 3.3.

Рассмотрим вычислительный пример, иллюстрирующий порядок действий по второму алгоритму.

Пример 3.2. Решить задачу ЛП:

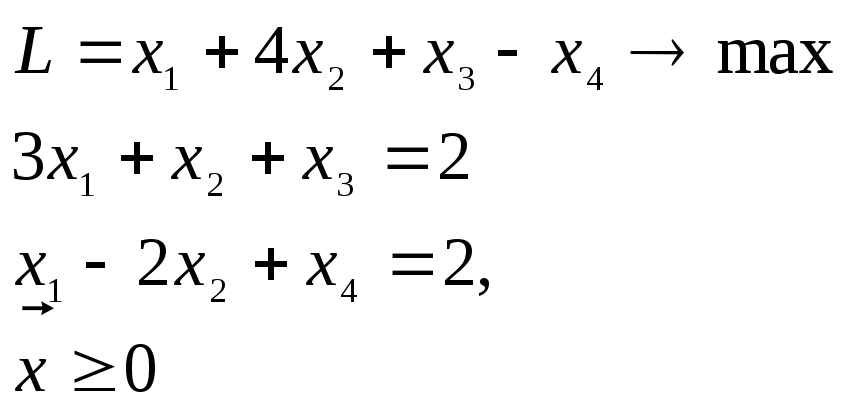
методом обратной матрицы, взяв в качестве исходного опорный план с базисом.

Вспомогательная таблица имеет вид:

Таблица 3.7 Вспомогательная таблица

№	b	A1	A2	A3	A4
1	2	3	1	1	0
2	2	1	-2	0	1
3	C	1	4	1	-1
4		1	-1	0	0
5		4	0	1	0

Для заполнения основной таблицы вычислим , обратную к. Так какединичная матрица, то. Базисные компоненты опорного плана. Параметрыопределяют по формулам:4

С учетом выполненных вычислений основная таблица имеет вид:

Таблица 3.8 Основная таблица

№	СS	FS	e0	e1	e2	A2	
1	1	A3	2	1	0	1	2
2	-1	A4	2	0	1	-2	---
3			0	1	-1	-1

Вычислив, анализируют ситуацию

так как среди есть отрицательный параметр, то

.

Множество, поэтому имеет место ситуация 3._достигается на первой строке таблицы. Получив k=2 и r=1 , строят базиснового опорного плана, для которого заполняют основную таблицу (табл. 3.9)

№	СS	FS	e0	e1	e2	Ak
1	4	A2	2	1	0
2	-1	A4	6	2	1
3			2	2	-1

Таблица 3.9 Конечная таблица

Вычислив для новые, получают, что

и имеет место ситуация 1. Оптимальный базис , оптимальный план прямой задачи X^*=(0,2,0,6), оптимальный план двойственной задачиОптимальное значение целевой функции (значение задачи) равно 2.

3.4. Определение начального опорного плана в симплекс-методе

3.4.1. Задачи ЛП с единичным базисом в матрице условий задачи (вариант 1). Значительное число задач эффективного распределения ограниченных активных средств описываются задачами ЛП в стандартной форме с неотрицательным вектором ограничений (). Записав задачу в канонической форме

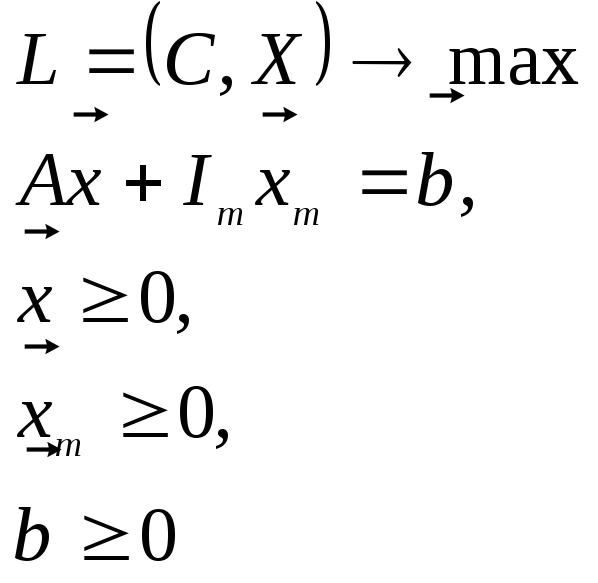
где - вектор искусственных переменных, введенных на этапе канонизации, I_m- единичная матрица размером m х m, получают опорный планзадачи (3.7) с базисом. Этот единичный базис и берут в качестве исходного при решении задачи (3.7) 1 или II алгоритмом метода последовательного улучшения плана.

Пример 3.3.Пусть задача ЛП задана в стандартной форме

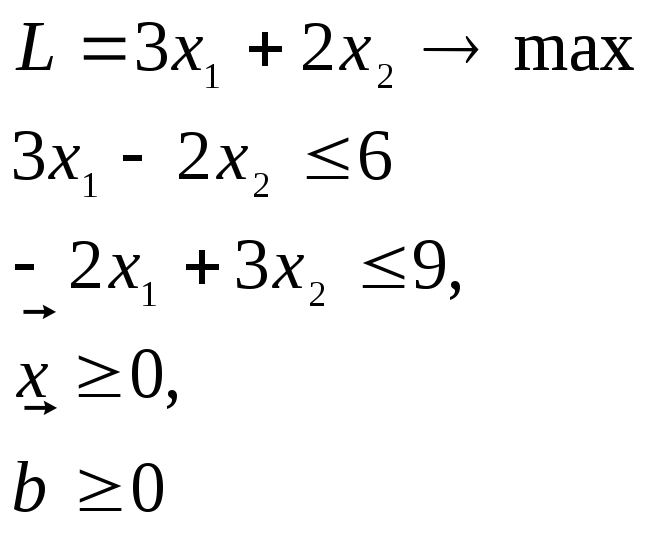
Записав задачу в канонической форме

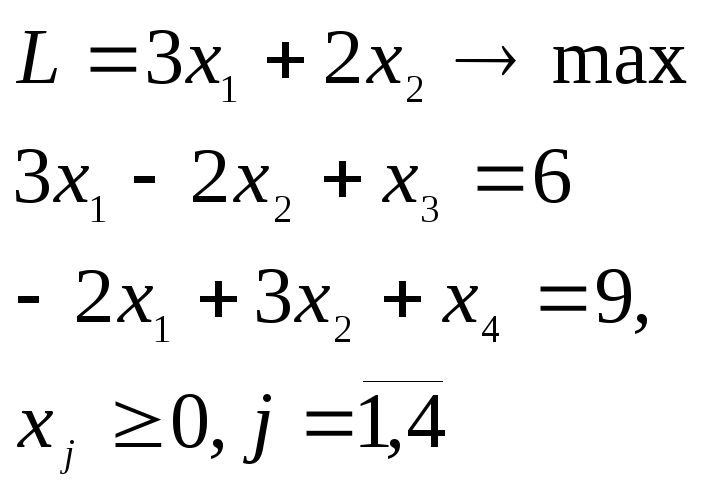
получают опорный план ее с единичным базисом.

Выбор искусственных векторов условий в качестве векторов исходного базиса соответствует, как правило, наихудшему начальному приближению, значительно удаленному от оптимальной вершины.

Указанный недостаток частично компенсируется отсутствием необходимости в проведении предварительных расчетов при заполнении исходных таблиц, связанных с вычислением обратной матрицы и матрицы X так как

3.4.2. Организация единичного базиса в условиях задачи ЛП

(Вариант II). Этот метод применяется , когда задача ЛП имеет вид

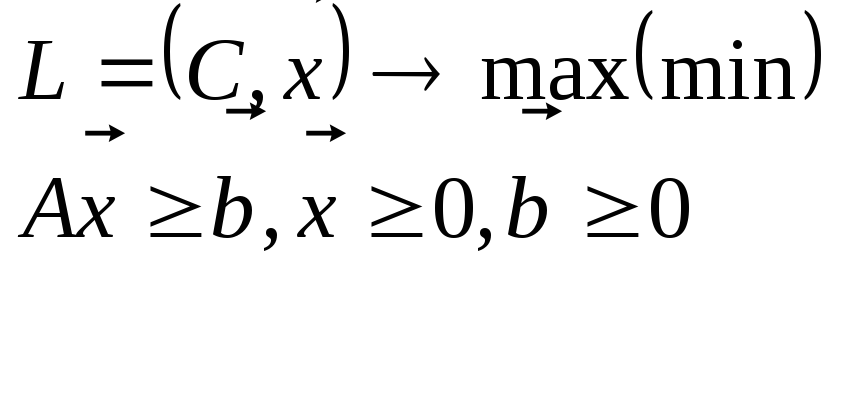
Записав условия задачи в форме равенств , получают систему векторовобразующих матрицу - I_m. Формирование единичного базиса осуществляют в три этапа.

1. Определяют среди компонент b_iвектора ограничениймаксимальную b_s

2. Каждое i -е условие умножают на (-1), и складывают с s-м условием. Результат записывают на место i -го условия. Таким образом, получают m-1 единичный вектор

3. Для получения недостающего единичного вектора в s-e условие добавляют неотрицательную переменную y , которую одновременно вычитают из целевой функции, предварительно умножив на достаточно большое неотрицательное число M. Полученная вспомогательная задача ЛП имеет в условиях единичный базис, , который и выбирают в качестве исходного при решении вспомогательной задачи 1 или II алгоритмом метода последовательного улучшения плана.

Пример 3.4.Организовать единичный базис в условиях задачи

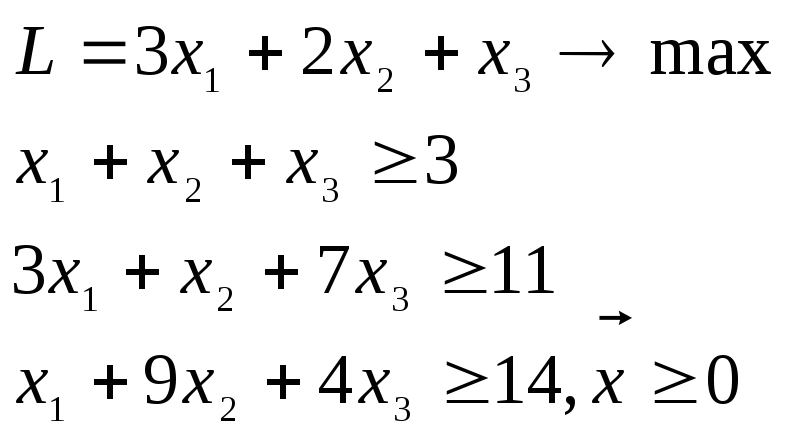
Записав задачу в канонической форме:

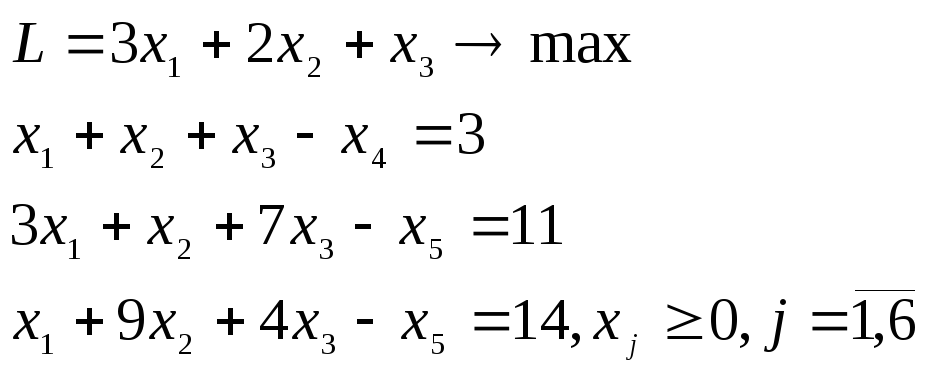
в соответствии с описанным алгоритмом определяют и формируют условия вспомогательной задачи (s=3)

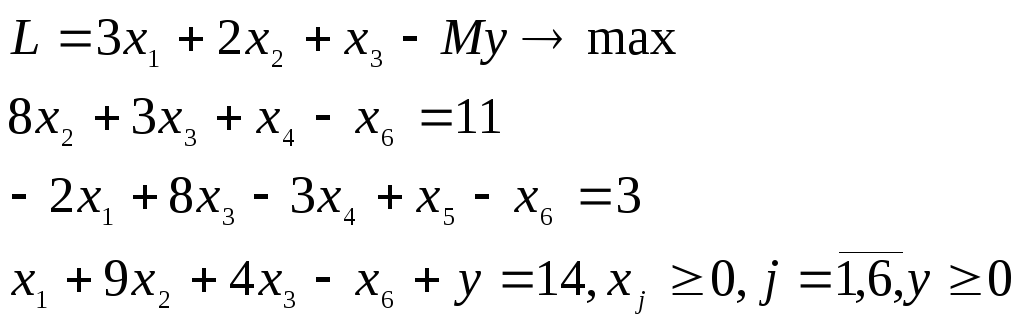
с единичным базисом опорного плана. При задании значения M необходимо ориентироваться на его нижнюю оценкуM:

,

где m- число ограничений, - максимальный по модулю элемент матрицы условий A ,- максимальный по модулю элемент вектора

3.4.3. Общие положения метода искусственного базиса (вариант III). При решении задачи ЛП методом искусственного базиса необходимо выполнить следующие этапы:

а) записать исходную задачу в канонической форме (3.1);

б) обеспечить неотрицательность вектора ограничений путем умножения левой и правой частей соответствующего i -го условия задачи (3.1) (b_i<0) на минус единицу;

в) построить вспомогательную задачу:

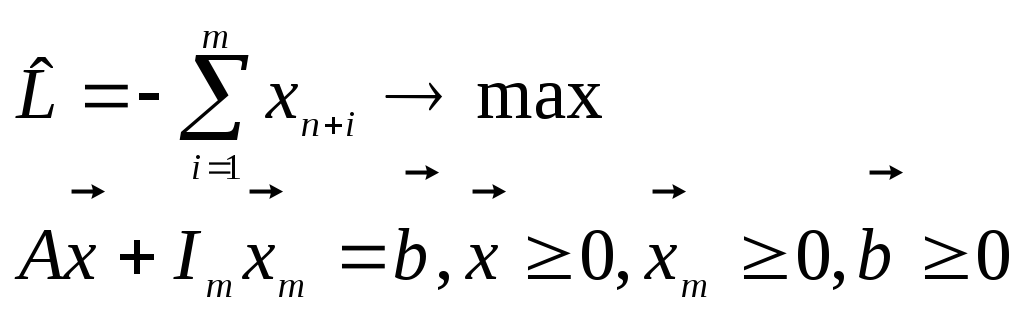, (3.8)

где , I_m- единичная матрица размеров mm ;

г) решить задачу (3.8) методом последовательного улучшения плана (I, II алгоритм), взяв в качестве исходного единичный базис , соответствующий опорному плану. Следует иметь ввиду, что множество планов задачи (3.8) не пусто иограничена сверху нулевым значением, поэтому процесс решения задачи (3.8) завершается определением оптимального планас оптимальным базисом.

д) осуществить анализ решения задачи (3.8), установив, какой из трех возможных случаев имеет место.

Случай 1.Оптимальное значение. В этом случае процесс решения задачи (3.1) прекращается, так как она неразрешима из-за несовместимости условий.

Случай 2.Оптимальное значениеи пересечение. В этом случаеявляется вырожденным опорным планом задачи (3.1), имеющим семейство F базисов. Взяв один из них, удовлетворяющий условию, переходят к этапу e.

Случай 3. Оптимальное значениеи пересечение. В этом случаес базисомберут в качестве исходного опорного плана задачи (3.1) и переходят к этапу e.

е) решить задачу (3.1) методом последовательного улучшения плана (1,П алгоритм), взяв в качестве исходного базис . Следует иметь в виду, что задача (3.1) может не иметь решения из-за неограниченности L сверху. Если она разрешима, то находится оптимальный планзадачи (3.1) с базисом.

3.4.4. Первый алгоритм метода искусственного базиса. При изучении первого алгоритма метода искусственного базиса следует иметь ввиду, что он представляет собой общую схему метода искусственного базиса, реализованную с учетом особенностей первого алгоритма метода последовательного улучшения плана.

Описание алгоритма:

а) записать исходную задачу ЛП в канонической форме (3.1) и обеспечить неотрицательность вектора ограничений ;

б) построить вспомогательную задачу (3.6) с матрицей условий , вектором ограничений, вектором коэффициентов линейной формы, имеющим N₁ = n+m компонент;

в) заполнить исходную симплекс-таблицу для единичного базиса задачи (3.8) (табл. 3.10). При заполнении таблицы следует иметь в виду, что матрицакоэффициентов разложения вектора ограничений, векторов условийпо единичному базису F_sсовпадает с матрицей, а параметры

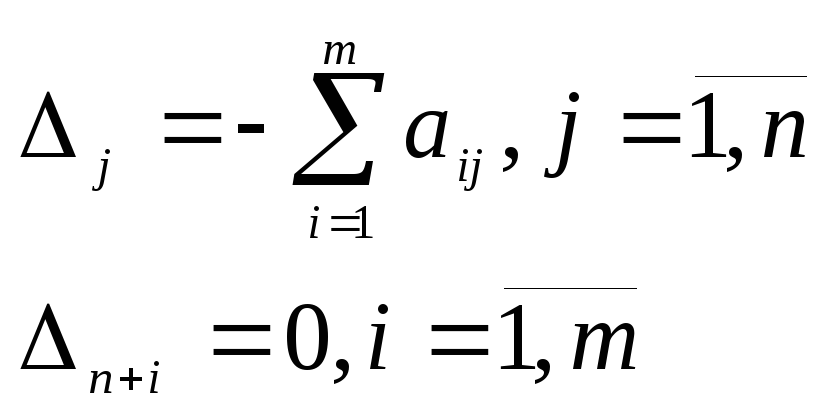
г) решить задачу ЛП с размерами вспомогательной задачи (3.8) первым алгоритмом метода последовательного улучшения плана;

д) осуществить анализ решения задачи (3.8). Если, то процесс решения задачи (3.1) прекращается. В этом случае каждое i -е условие задачи (3.1), для которого, находится в противоречии с остальными условиями, а исходная задача неразрешима из-за несовместимости условий.

Если . тоявляется опорным планом задачи (3.1) с базисомв этом случае переходят к этапу «ж». Еслии, тоявляется вырожденным опорным

Таблица 3.10 Исходная симплекс-таблица.

			C	0	...	0	...	0	-1	...	-1
№	Cs	Fs	A0	A1	...	Ak	...	An	An+1	...	An+m	
1	-1	An+1	b1	a11	...	a1k	...	a1n	1	...	0
...	...	...	...	...	...	...	...	...	...	...	...
R	-1	An+r	br	ar1	...	ark	...	arn	0	...	0	
...	...	...	...	...	...	...	...	...	...	...	...
m	-1	An+m	bm	am1	...	amk	...	amn	0	...	1
m+1			Z0		...		...		0	...	0

планом задачи (3.1) с семейством базисов F. В этом случае переходят к этапу «e» ,

е) сформировать базис , соответствующий вырожденному опорному планузадачи (3.1). Необходимо для каждого векторапроверить, есть ли ненулевые элементыв i -и строке,оптимальной таблицы вспомогательной задачи. Если нет, то i-я строка вычеркивается из таблицы, а векторвыводится из базисаЕсли элементсуществует, то

вектор вводится в базис вместо,и таблица пересчитывается по формулам, связывающим параметры двух последовательных симплекс-таблиц.

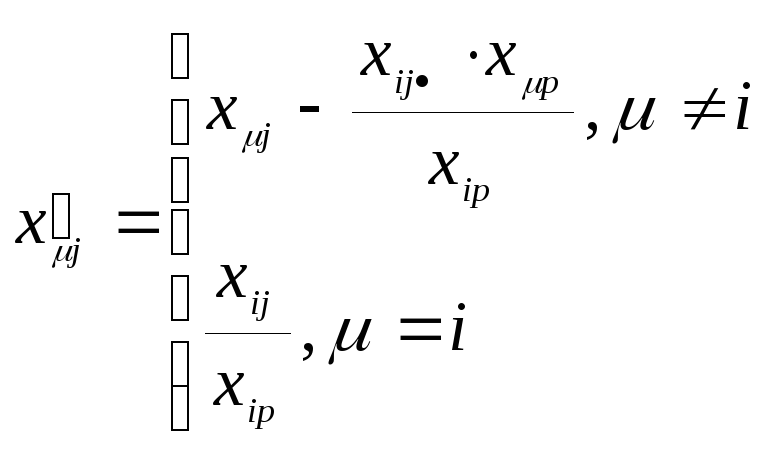
где . Указанные действия необходимо повторять до тех пор, пока не находят базис, пересечение которого с F_Sпусто. В этом случае переходят к этапу «ж».

ж) заполнить исходную симплекс таблицу для решения задачи (3.1). Необходимо взять N=n, M=M1 , , где M1 -число векторов в базисе,- вектор коэффициентов линейной формы исходной задачи. Сформировать для базисавектор C_S, коэффициенты- разложений вектора ограничений и векторов условий задачи (3.1) по базисунеобходимо выбирать из оптимальной таблицы задачи (3.6).

Параметры определяют по формулам (3.3).

3. Решить задачу ЛП с размерами M N, M=M1, N=n, первым алгоритмом метода последовательного улучшения плана. Начальному опорному плану задачи, соответствует симплекс таблица, заполненная на этапе «ж». Если в процессе решения (3.1) возникла ситуация 2, то исходная задача неразрешима из-за неограниченности L на множестве планов. Если (3.1) разрешима, то находится ее оптимальный планс оптимальным базисом.

Пример 3.5. Задачу ЛП

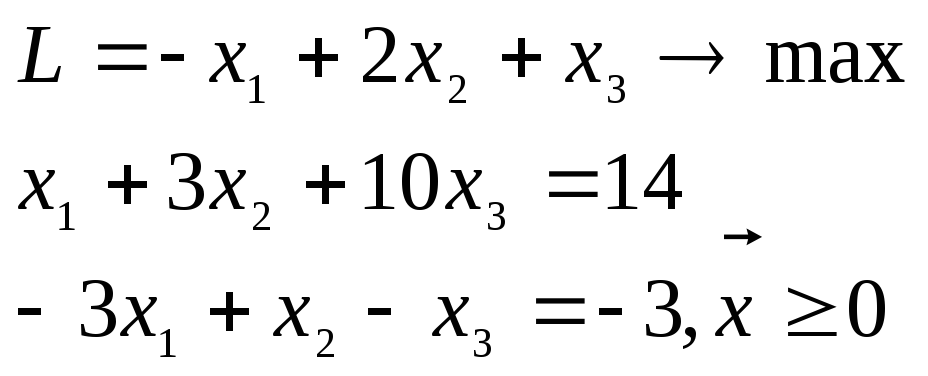
решить первым алгоритмом метода искусственного базиса.

1. Приведение задачи к требуемой форме. Исходная задача задана в канонической форме (3.1), но вектор ограничений не удовлетворяет условиям неотрицательности. Умножив второе условие на (-1), приводят ее к требуемой форме записи:

,

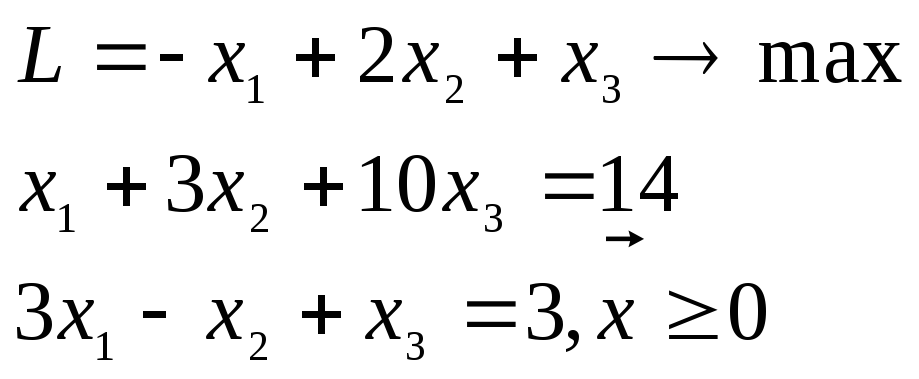где

2. Построение вспомогательной задачи. Вводя искусственные неотрицательные переменные x₄, x₅, получают вспомогательную задачу (3.8)

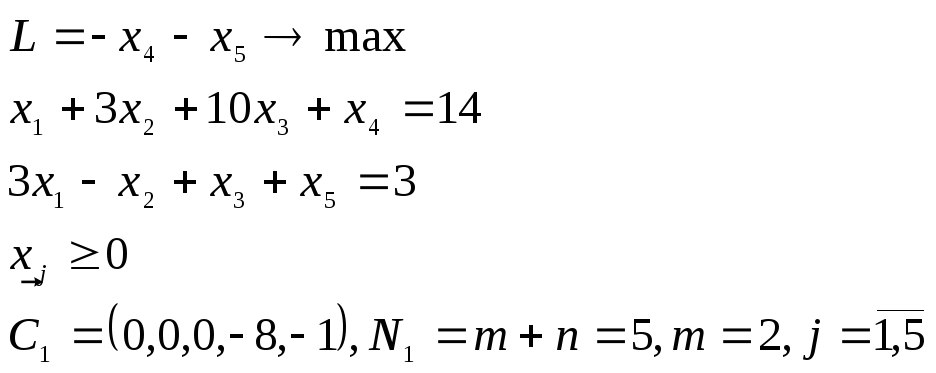
3. Заполнение исходной симплекс таблицы (табл. 3.7) вспомогательной задачи, соответствующей единичному базису (табл. 3.11)

Таблица 3.11 Исходная таблица

			C	0	0	0	-1	-1
№	Cs	Fs	A0	A1	A2	A3	A4	A5	
1	-1	A4	14	1	3	10	1	0	1,4
2	-1	A5	3	3	-1	1	0	1	3
3			-17	-4	-2	-11	0	0

4. Решение вспомогательной задачи первым алгоритмом метода последовательного улучшения плана. Решение начинается с анализа ситуаций в начальной таблице

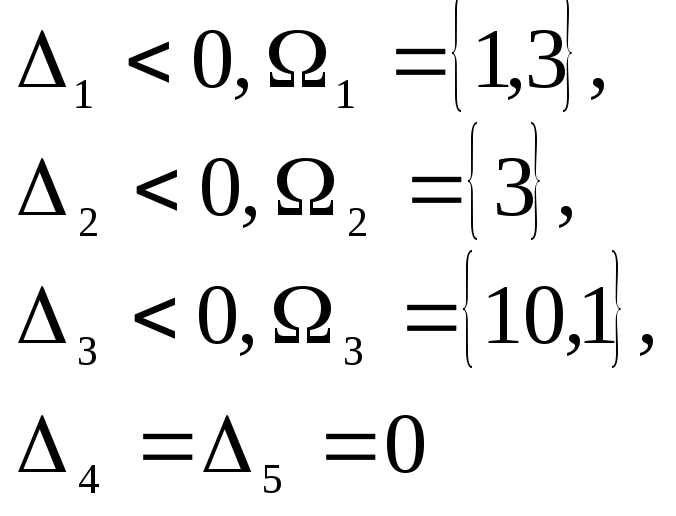
Имеет место ситуация 3. Применяя приближенный метод определения k,. Параметр_, r = 1. Для k=3, r=1 заполняют новую таблицу (табл. 3.12 )

Таблица 3.12 Первая таблица

№	Cs	Fs	A0	A1	A2	A3	A4	A5	
1	0	A3	1,4	0,1	0,3	1	0,1	0	14
2	-1	A5	1,6	2,9	-1,3	0	-0,1	1	16,29
3			-1,6	-2,9	1,3	0	1,1	0

Так как , то имеет место ситуация 3, для которой r=1,r=2 . Заполняют новую таблицу (табл. 3.13)

Таблица 3.13 Оптимальная таблица

№	Cs	Fs	A0	A1	A2	A3	A4	A5
1	0	A3	39,29	0	10,29	1	3,29	-1(29
2	0	A1	16,29	1	-13(29	0	-1(29	10,29
3			0	0	0	0	1	1

Так как , то имеет место ситуация 1 иявляется решением вспомогательной задачи с базисоми значением.

5. Анализ решения вспомогательной задачи. Так как

, то является опорным планом исходной задачи с базисом.

6. Заполнение начальной симплекс-таблицы для решения основной задачи осуществляется на основе оптимальной (табл.3.14) таблицы вспомагательной задачи и вектора 7. Решение основной задачи первым алгоритмом метода последовательного улучшения плана. Оно начинается с анализа ситуации для начальной таблицы. Так как, то имеет место ситуация 3, для которой k=2, r=1. Новая таблица имеет вид таблицы 3.15

Таблица 3.14 Исходная таблица основной задачи

			C	-1	2	1
№	Cs	Fs	A0	A1	A2	A3	
1	1	A3	39,29	0	10,29	1	39,10
2	-1	A1	16,29	1	-13,29	0	---
3			23,29	0	-35,29	0

Таблица 3.15 Конечная таблица

№	Cs	Fs	A0	A1	A2	A3
1	2	A2	3,9	0	1	2,9
2	-1	A1	0,3	1	0	1,3
3			5,5	0	0	3,5

Так как , то имеет место ситуация 1 и

3.4.5. Второй алгоритм метода искусственного базиса. При изучении второго алгоритма метода искусственного базиса следует иметь в виду, что он представляет собой общую схему метода искусственного базиса, реализованную с учетом особенностей метода обратной матрицы. Для решения задачи этим методом необходимо выполнить следующие этапы:

а) записать исходную задачу в канонической форме (3.1) и обеспечить неотрицательность вектора ограничений ;

б) построить вспомогательную задачу (3.8) с матрицей условий (А, I_m), вектором ограничений, вектором коэффициентов линейной формы, имеющим N₁=n+m компонент ;

в) заполнить вспомогательную таблицу (табл. 3.16) для задачи (3.8).

г) заполнить основную таблицу (табл. 3.17) для задачи (3.8), соответствующую исходному единичному базису .

Таблица 3.16 Вспомогательная таблица

№	b	A1	A2	...	An	An+1	...	An+m
1	b1	a11	a12	...	a1n	1	...	0
2	b2	a21	a22	...	a22	0	...	0
...	...	...	...	...	...	...	...	...
m	bm	am1	am2	...	amn	0	...	1
m+1	C	0	0	...	0	-1	...	-1
m+2				...		0	...	0
...	...	...	...	...	...	...	...	...
m+2+l				...			...

Таблица 3.17 Начальная основная таблица

№	CS	FS	e0	e1	...	em	Ak	
1	-1	An+1	b1	1	...	0	x1k
2	-1	An+2	b2	0	...	0	x2k
...	...	...	...	...	...	...	...
r	-1	An+r	br	0	...	0	xrk	
...	...	...	...	...	...	...	...
m	-1	An+m	bm	0	...	1	xmk
M+1					...	m

Следует иметь в виду, что базисные компоненты начального опорного плана совпадают с компонентами вектора ограничений. Так как, то.

д) решить задачу ЛП с размерами M N, M=m, N=N₁, вспомогательной задачи вторым алгоритмом метода последовательного улучшения плана;

е) осуществить анализ решения вспомогательной задачи.

Если , то процесс решения задачи (3.1) прекращается из-за несовместности ее условий. Еслитоявляется опорным планом задачи (3.1) с базисом. В этом случае переходят к этапу "Ж".

Если и пересечение, то

является вырожденным опорным планом задачи с семейством базисов F.

В этом случае необходимо выполнить построение базиса , опорного планав соответствии с правилами этапа "E" первого алгоритма метода искусственного базиса, имея в виду, чтои перейти к выполнению этапа "Ж".

ж) заполнить начальную вспомогательную таблицу для исходной задачи на основе табл 3.9. Число столбцов ее N=n, M=M1, , где M1 - число векторов в базисе.В m+1 строку таблицы заносятся элементы вектора,

з) заполнить начальную основную таблицу для исходной задачи (3.1) на основе оптимальной таблицы (3.10) для вспомогательной задачи, в которой столбцы остаются прежними, столбецзаполняется в соответствии с. Элементыстроки вычисляются по формуле.

к) решить исходную задачу ЛП с размерами M N, M=M₁, N=n методом обратной матрицы. Начальному опорному планузадачи (З.1) соответствуют заполненные на этапах "Е", "Ж" вспомогательная и основная таблицы. Если в процессе решения возникла ситуация 2, то (3.1) неразрешима из-за неограниченности сверху линейной формы L. В противном случае находят оптимальный план, оптимальный бaзиси значениезадачи.

Пример 3.6.

Задачу ЛП

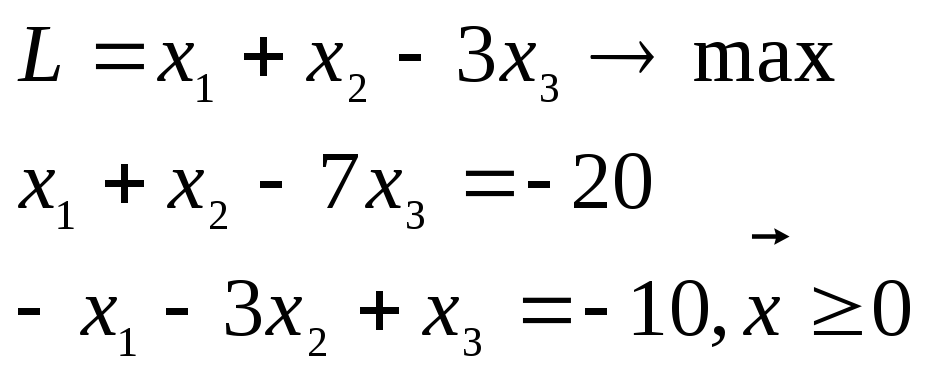
решить вторым алгоритмом метода искусственного базиса.

1. Приведение задачи к требуемой форме.

Задача записана в канонической форме, но не удовлетворяет условиям неотрицательности. Умножив первое и второе условие на минус единицу, получают исходную задачу в требуемой форме

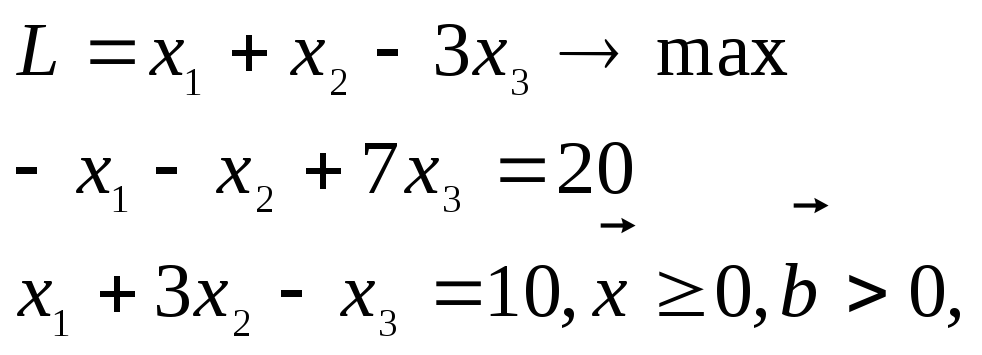
где .

2. Построение вспомогательной задачи.

Вводятся дополнительные неотрицательные переменные x₄, x₅и задача (3.8) принимает вид:

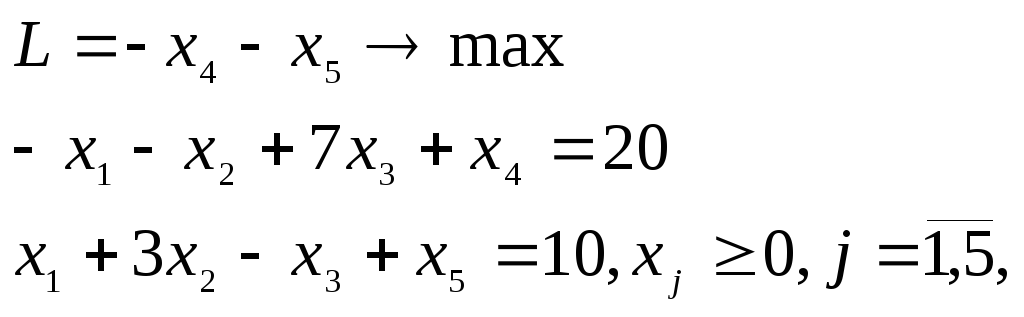
где .

3. Заполнение вспомогательной таблицы (табл. 318)

Таблица 3.18 Вспомогательная таблица

№	b	A1	A2	A3	A4	A5
1	20	-1	-1	7	1	0
2	10	1	3	-1	0	1
3	C2	0	0	0	-1	-1
4		0	-2	-6	0	0
5		-6,7	-20,7	0	6,7	0
6		0	0	0	1	1

В 4, 5, 6-й строках таблицы записаны значения параметров по итерациям.

4. Заполнение основной таблицы вспомогательной задачи, соответствующей единичному базису (табл. 3.19)

Таблица 3.19 Начальная основная таблица

№	СS	FS	e0	e1	e2	A3	
1	-1	A4	20	1	0	7	20,7
2	-1	A5	10	0	1	-1	---
3			-30	-1	-1	-6

5. Решение вспомогательной задачи методом обратной матрицы.

Вычисляя , получают.Применяя приближенный метод, получают k=3. Так как, то r=1. Заполняют новую таблицу (табл. 3.20).

Вычисляя , получают. Так как k=2, то r=2. Заполняют новую таблицу (табл. 3.21).

Таблица 3.20 Первая основная таблица

№	СS	FS	e0	e1	e2	A2	
1	0	A3	20,7	1,7	0	-1,7	---
2	-1	A5	90,7	1,7	1	20,7	9,2
3			-90,7	-1,7	-1	-20,7

Таблица 3.21 Оптимальная основная таблица

№	СS	FS	e0	e1	e2
1	0	A3	7,2	3,20	1,20
2	0	A2	9,2	1,20	7,20
3			0	0	0

Вычисляя , получают. Имеет место ситуация 1, поэтому.

6. Анализ решения вспомогательной задачи. Так как ,, тоявляется опорным планом основной задачи с базисом

7. Построение исходной вспомогательной таблицы (табл. 3.22) основной задачи производится на основе вспомогательной таблицы вспомогательной задачи отбрасыванием столбцов A₄, A₅и заменойна.

В 4,5-ю строки таблицы заносят значения параметров

8. Заполнение начальной основной таблицы исходной задачи (табл. 3.23) осуществляют на основе оптимальной таблицы вспомогательной задачи, в которой столбцы F_S, e₀, e₁, e₂остаются прежними, столбец C_S формируют в соответствии с.

9. Решение основной задачи методом обратной матрицы. Вычисляют . Так как k=1,, то r=2. Заполняют новую таблицу (табл. 3.24).

Таблица 3.22 Вспомогательная таблица

№	b	A1	A2	A3
1	20	-1	-1	-1
2	10	1	3	-1
3	C1	1	2	-3
4		-2,5	0	0
5		0	1,3	0

Таблица 3.23 Начальная основная таблица

№	СS	FS	e0	e1	e2	A1	
1	-3	A3	7,2	3,20	1,20	-0,1	---
2	2	A2	9,2	1,20	7,20	0,3	15
3			-3,2	-7,20	11,20	-0,4

Таблица 3.24 Конечная основная таблица

№	СS	FS	e0	e1	e2
1	-3	A3	5	1,6	1,6
2	1	A1	15	1,6	7,6
3			0	-1,3	2,3

Вычисляя , получают. Имеет место ситуация 1, поэтому. Значение задачи.

3.4.6. Общие положения М-метода (Вариант IV). При решении задачи ЛП M-методом необходимо выполнить следующие этапы:

а) записать исходную задачу в канонической форме (3.1);

б) обеспечить неотрицательность вектора ограничений путем умножения левой и правой частей i -го условия задачи (3.1), для которого b _i<0, на минус единицу;

в) построить вспомогательную задачу (М-задачу)

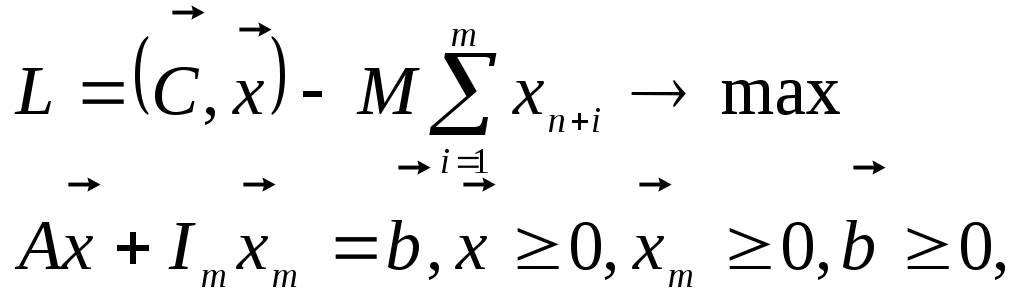
где I_m- единичная матрица размером mm,- неотрицательный вектор искусственных переменных, М - положительное число, превосходящее по величине любое сравниваемое с ним другое число.

г) решить задачу (3.9) методом последовательного улучшения плана (1, 11 алгоритм), взяв в качестве исходного единичный базис опорного плана. При решении задачи (3.9) следует иметь в виду, что величина М не фиксирована иявляются функциями параметра М. В связи с этим необходимо:

1. Вектор коэффициентов линейной формы задачи (3.9) представить в виде линейной зависимости от М.

где .

2. При вычислении и анализе пользоваться их линейной зависимостью

(3.10)

где

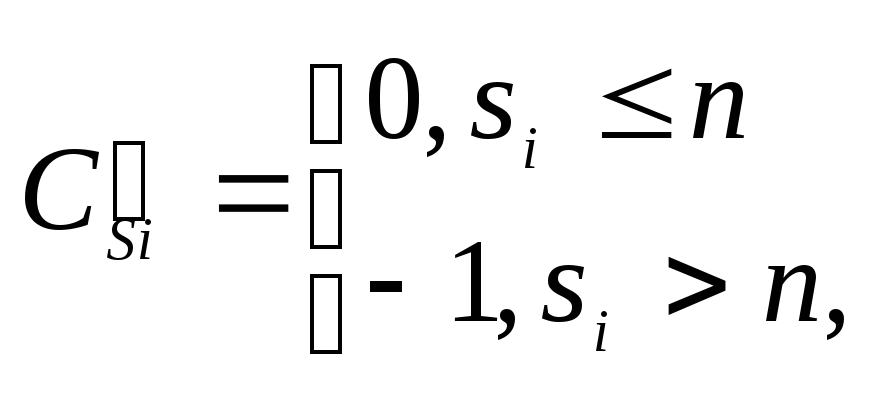
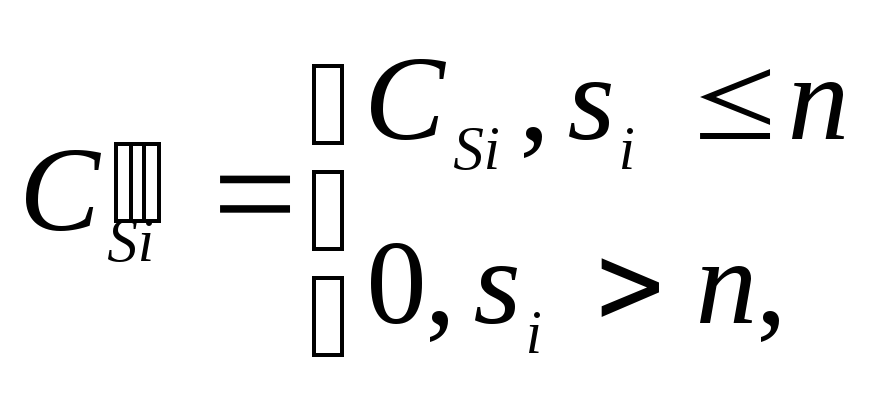
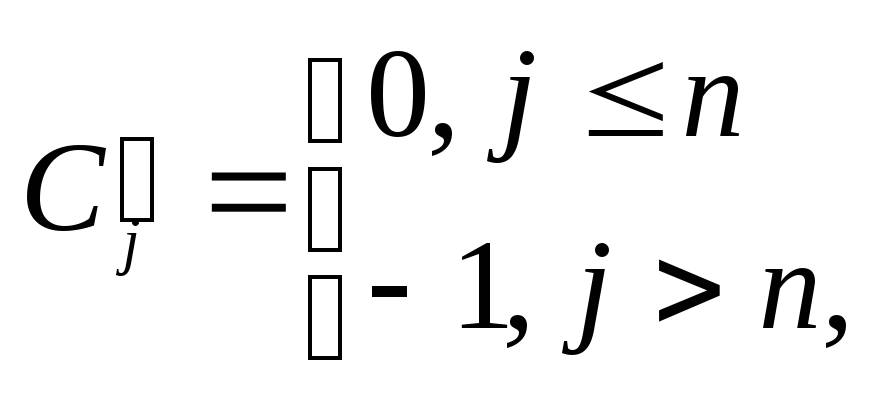
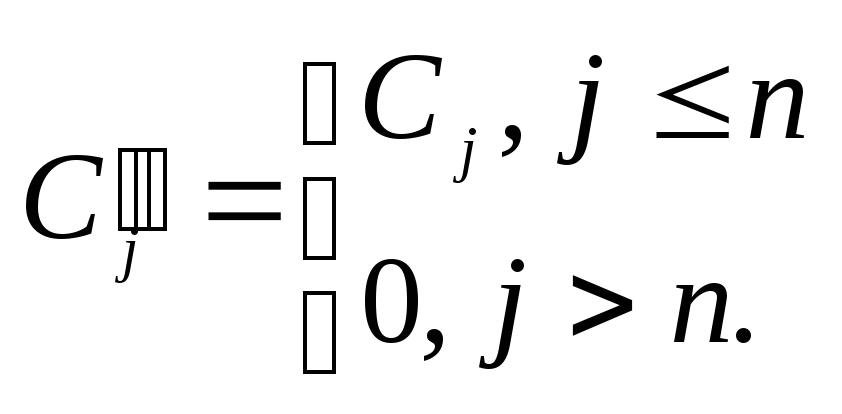
3. Знаки параметров определяют на основе знаков параметровзависимости (3.10):

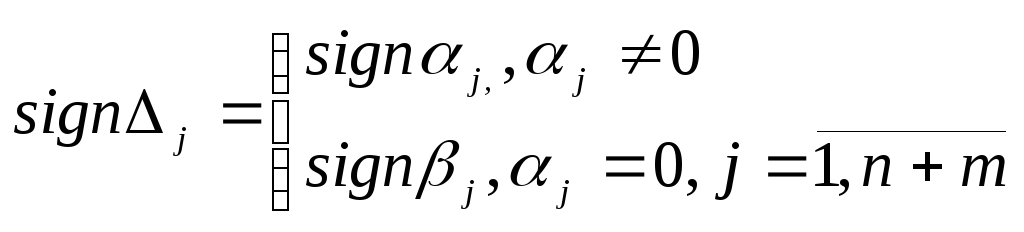
Если в процессе решения задачи (3.9) возникла ситуация 2, то задача (3.1) неразрешима из-за неограниченности L сверху. В противном случае находят оптимальный план и оптимальный базисзадачи (3.9).

д) осуществить анализ решения М-задачи, установив, какой из трех возможных случаев имеет место:

Случай 1.Все. В этом случаeявляется решением задачи (3.1) с оптимальным базисом. Значение задачи (3.1) равно.

Случай 2.ВсеВ этом случаеявляется вырожденным опорным планом задачи (3.1) с конечным семейством F оптимальных базисов. В качествеберут любой из них, удовлетворяющий условию.

Случай 3.Средиесть строго положительные числа. В этом случае задача (З.1) неразрешима из-за несовместимости условий.

3.4.7. Первый алгоритм M-метода. При изучении первого алгоритма М-метода следует иметь в виду, что он представляет собой первый алгоритм метода последовательного улучшения плана, модифицированный с учетом особенностей М-задачи. Для решения задачи первым алгоритмом М-метода необходимо выполнить следующие этапы:

а) записать исходную задачу в канонической форме (3.1) и обеспечить неотрицательность вектора ограничений;

б) построить М-задачу (3.9) с матрицей условий (A,I_m) , вектором ограничений, вектором коэффициентов линейной формы, имеющим n+m компонент;

в) заполнить исходную таблицу М-задачи (табл. 3.25) для единичного базиса

При заполнении таблицы следует иметь в виду, что матрица X - коэффициентов разложений совпадает с матрицей

Таблица 3.25 Исходная таблица М-метода

					0	...	0	-1	...	-1
					С1	...	Сn	0	...	0
№			FS	A0	A1	...	An	An+1	...	An+m	
1	-1	0	An+1	b1	a11	...	a1n	1	...	0
...	...	...	...	...	...	...	...	...	...	...
R	-1	0	An+r	br	ar1	...	arn	0	...	0	
...	...	...	...	...	...	...	...	...	...	...
m	-1	0	An+m	bm	am1	...	amn	0	...	1
m+1						...	n	0	...	0
m+2						...	n	0	...	0

г) проверить наличие ситуации 1, для которой . Если ситуация 1 имеет место, то переходят к "Л", иначе – к "Д";

д) проверить наличие ситуации 2, для которой существует и. Если ситуация 2 имеет место, то процесс решения М-задачи прекращается и делается заключение о том, что исходная задача (З.1) неразрешима из-за неограниченности L сверху. В противном случае переходят к "Е".

е) применяя точный или приближенный метод, находят "К" – номер направляющего столбца;

ж) определяются позиции базиса, на которых достигается и находится номер направляющей строкиr.

з) построить новый базис F_S, векторыпутем замены A_Srна A_k,на, на;

е) вычислить элементы таблицы, соответствующей новому опорному плану по формулам:

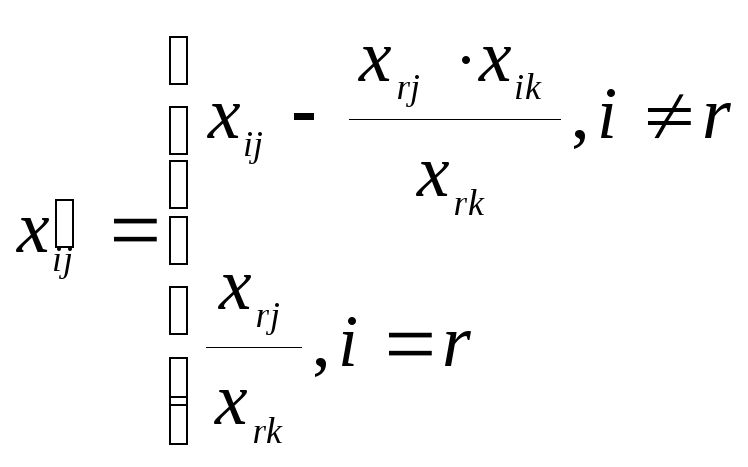
где и перейти к выполнению этапа "Г”;

д) осуществить анализ решения М-задачи в соответствии с этапом "Д” общей схемы М-метода.

Пример 3.7.

Задачу ЛП

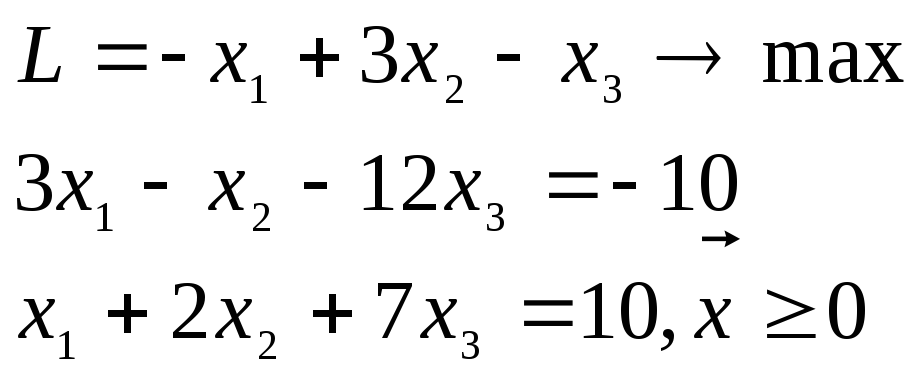
решить первым алгоритмом М-метода.

1. Приведение задачи к требуемой форме. Задача задана в канонической форме, но вектор ограничений не удовлетворяет условиям неотрицательности. Умножив первое ограничение на (-1), получают исходную задачу в требуемой форме:

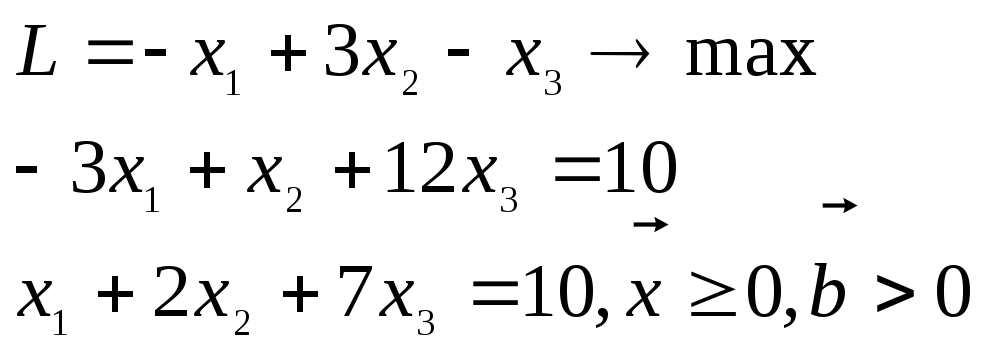
2. Построение М-задачи. Вводят неотрицательные, искусственные переменные и строят М-задачу:

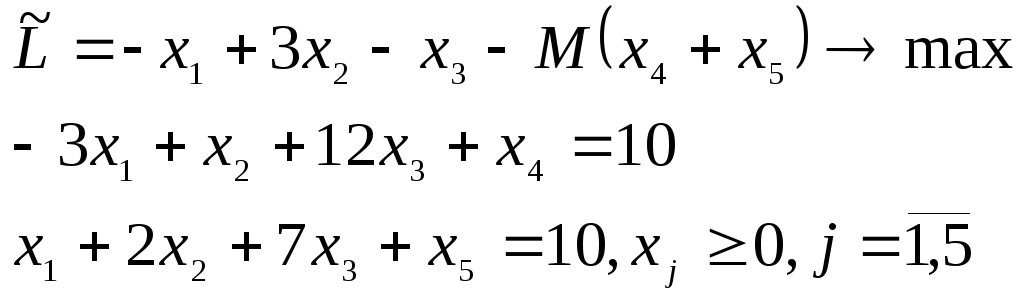
3. Заполнение исходной таблицы для единичного базиса М-задачи (табл. 3.26).

4. Анализ исходной таблицы. Так как , то имеет место ситуация 3. Применяя приближенный метод, получают, что k=3 , тогда r=1.

5. Заполнение таблицы для базиса . (табл. 3.27)

Таблица 3.26. Исходная симплекс-таблица

					0	0	0	-1	-1
					-1	3	-1	0	0
№			FS	A0	A1	A2	A3	A4	A5	
1	-1	0	A4	10	-3	1	12	1	0	5,6
2	-1	0	A5	10	1	2	7	0	1	10,7
3				-20	2	-3	-19	0	0
4				0	1	-3	1	0	0

Так как , то имеет место ситуация 3, при этом k=2 и r=2 .

6. Заполнение таблицы для базиса (табл. 3.28)

Так как , то имеет место

Таблица 3.27 Первая таблица

№			FS	A0	A1	A2	A3	A4	A5	
1	0	-1	A3	5,6	-1,4	1,12	1	1,12	0	10
2	-1	0	A5	25,6	33,12	17,12	0	-4,12	1	50,17
3				-25,6	-33,12	-17,12	0	19,12	0
4				-5,6	5,4	-37,12	0	-1,12	0

Таблица 3.28 Конечная таблица

№			FS	A0	A1	A2	A3	A4	A5	
1	0	-1	A3	10,17	-7,17	0	1	2,17	-1,17
2	0	3	A2	50,17	33,17	1	0	-7,17	12,17
3				0	0	0	0	1	1
4				140,17	123,17	0	0	259,17	37,17

ситуация 1. Вектор является решением M-задачи. Оптимальный базис. Число итераций при движении в оптимальную вершину существенно сокращается, если при выбореkиспользовать точный метод. Однако при этом существенно возрастает трудоемкость преобразования информации в пределах одной итерации.

7. Анализ решения M - задачи. Так как ине содержит искусственных векторов условий, тоявляется решением исходной задачи,, значение задачи.

3.4.8. Второй алгоритм М-метода. При изучении второго алгоритма М - метода следует иметь в виду, что он представляет собой метод обратной матрицы, модифицированный с учетом особенностей М - задачи. Для решения задачи вторым алгоритмом М - метода необходимо выполнить следующие этапы:

а) записать исходную задачу в канонической форме (3.1) и обеспечить неотрицательность вектора ограничений;

б) построить М-задачу (3.9), записать для нее вспомогательную таблицу (табл. 3.29)

Таблица 3.29 Вспомогательная таблица М-метода

№	b	A1	...	An	An+1	...	An+m
1	b1	a11	...	a1n	1	...	0
...	...	...	...	...	...	...	...
M	bm	am1	...	amn	0	...	1
m+1		0	...	0	-1	...	-1
m+2		С1	...	Сn	0	...	0
m+3			...		0	...	0
m+4			...		0	...	0
...	...	...	...	...	...	...	...
m+3+l			...			...
m+4+l			...			...

и основную таблицу, взяв в качестве исходного единичный базис (табл. 3.30)

В m+1 и m+2 строки таблицы заносят компоненты векторов изависимостигде;

в) вычислить._jи_jпо формулам

и занести их в m+3 и m+4 строки вспомогательной таблицы;

г) проверить наличие ситуaции 1, для которой все . Если ситуация 1 имеет место, то процесс решения М-задачи прекращается и переходят к этапу "М". В противном случае выполняют этап "Д”;

д) определить, применяя точный или приближенный метод, номер kнаправляющего столбца;

Таблица 3.30 Основная таблица М-метода

№			FS	e0	e1	...	em	Ak	
1	-1	0	An+1	b1	1	...	0	x1k
2	-1	0	An+2	b2	0	...	0	x2k
...	...		...	...	...	...	...	...
r	-1	0	An+r	br	0	...	0	xrk	
...	...	...	...	...	...	...	...	...
m	-1	0	An+m	bm	0	...	1	xmk
m+1			’		-1	...	-1	
m+2			”	0	0	...	0	

е) заполнить столбец , занося в m+1 строку его значение_k а в m+2 строку значение_k. В остальные строки столбца заносят коэффициенты разложения

ж) проверить наличие ситуации 2, для которой . Если ситуация 2, имеет место, то процесс решения М-задачи прекращается и делается заключение о неразрешимости задачи (3.1) из-за неограниченности L сверху. В противном случае выполняют этап "з";

з) определить позиции, на которых достигается и номерrнаправляющей строки таблицы;

к) построить новый базис F_S, векторыпутем замены A_Srна A_k,на,на;

е) вычислить элементы новой основной таблицы по формулам:

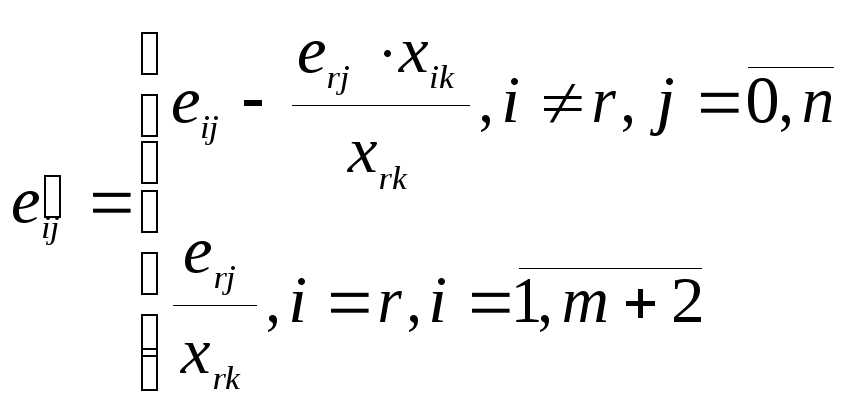
и перейти к выполнению этапа "В".

м) осуществить анализ решения М-задачи в соответствии с этапом "Д” общей схемы М-метода.

Пример 3.8.

Решить задачу ЛП

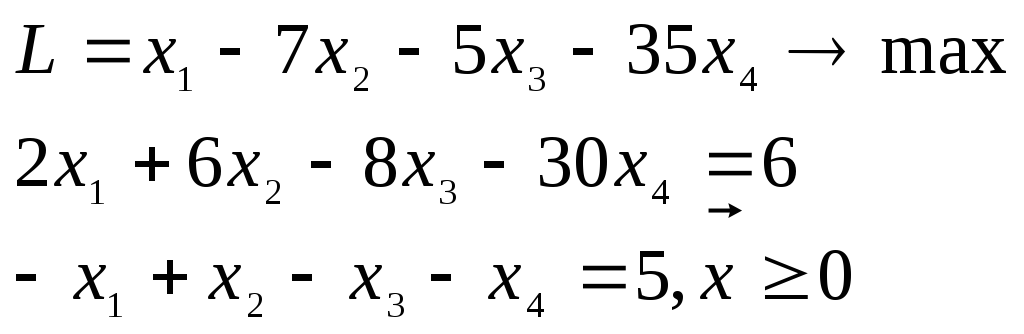
вторым алгоритмом М-метода.

Так как задача в канонической форме и b0, то решение начинают с построения М-задачи.

1. Построение М-задачи

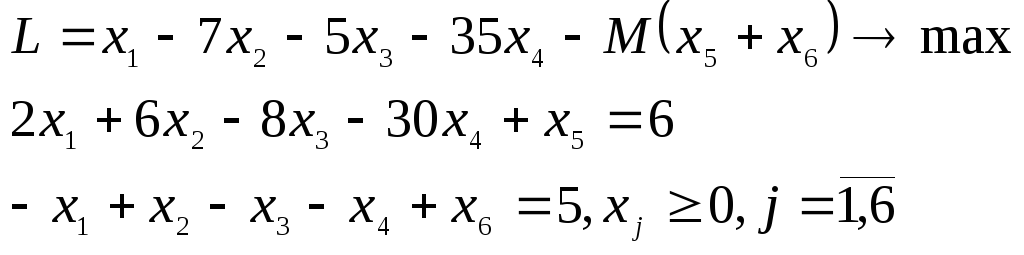
2. Заполнение вспомогательной (табл. 3.31) и основной (табл. 3.32) таблиц для плана 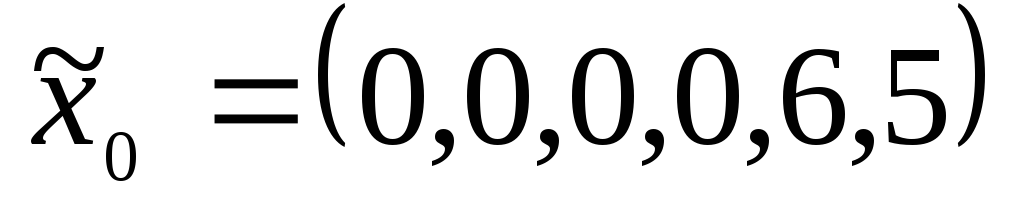единичным базисом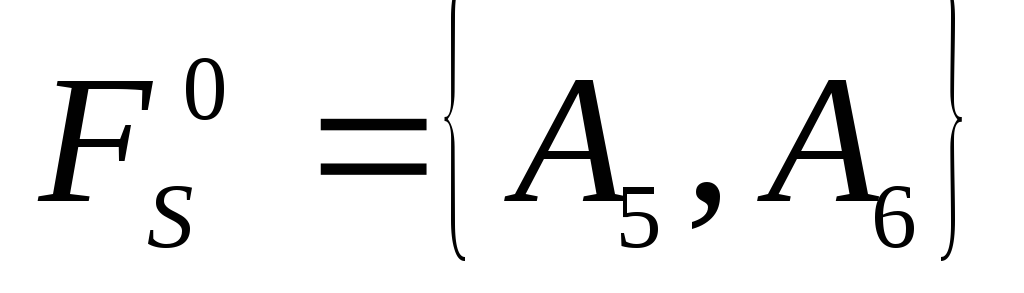

3. Вычисляют и, получают . Так как k=2,, то r=1.

4. Заполняют, основную таблицу для базиса (табл. 3.33)

5. Вычисляют и, получают. Так как k=4,, то r=2.

6. Заполняют основную таблицу для базиса 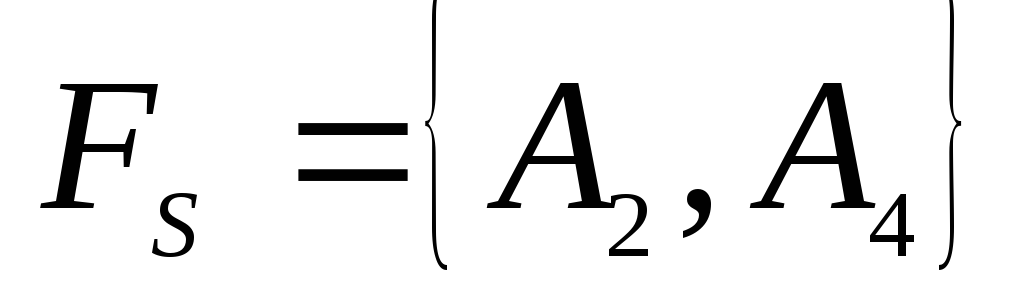(табл. 3.34)

7. Вычисляют и, получают.Имеет место ситуация 1, поэтому

Таблица 3.31 Вспомогательная таблица

№	b	A1	A2	A3	A4	A5	A6
1	6	2	6	-8	-30	1	0
2	5	-1	1	-1	-1	0	1
3		0	0	0	0	-1	-1
4		1	-7	-5	-35	0	0
5		-1	-7	9	31	0	0
6		-1	-7	5	35	0	0
7		4,3	0	-1,3	-4	7,6	0
8		-10,3	0	43,3	70	-7,6	0
9		0	0	0	0	1	1
10		20	0	17,2	0	7,4	-35,2

Таблица 3.32 Основная таблица

№			FS	e0	e1	e2	A2	
1	-1	0	A5	6	1	0	6	1
2	-1	0	A6	5	0	1	1	5
3			’	-11	-1	-1	-7
4			”	0	0	0	

Таблица 3.33 Первая основная таблица

№			FS	e0	e1	e2	A2	
1	0	-7	A2	1	1,6	0	-5	---
2	-1	0	A6	4	-1,6	1	4	1
3			’	-4	1,6	-1	-4
4			”	-7	-7,6	0	10

8. Анализ решения М-задачи. Так как не содержит искусственных векторов, то, оптимальный базис, значение целевой функции задачи равно -77.

Таблица 3.34 Конечная таблица

№			FS	e0	e1	e2
1	0	-7	A2	6	-1/24	5/4
2	0	-35	A4	1	-1/24	1/4
3			’	0	0	0
4			”	-77	7/4	-70/4

3.5. Метод последовательного уточнения оценок (первый алгоритм)

При применении данного метода задачу ЛП необходимо представить в канонической форме (3.1). Кроме того, необходимо указать опорный план двойственной задачи

с базисом. Последовательное продвижение по базисам опорных планов задачи (3.11) вплоть до получения оптимального базиса, ее решениесоставляет идея метода последовательного улучшения оценок. Первый алгоритм начинается с заполнения таблицы для исходного базиса F_S . Процесс заполнения m+1 строк таблицы полностью совпадает с процессом заполнения табл. 3.1, описанным в 3.2. Заполненная таблицa (табл. 3.35) имеет вид:

Строка табл. 3.35 служит для выбора k - номера направляющего столбца.

Движение в оптимальную вершину двойственной задачи (переход от исходной таблицы к последующей) начинают с установления наличия ситуации 1, для которой базисные компоненты псевдоплана должны быть неотрицательными числами:Если средиесть отрицательные, то для каждого<0 проверяют наличие ситуации 2:

Если существует для которого, то задача (3.11)

неразрешима из-за неограниченности снизу, при этом условия задачи (3.1) несовместны. Если ситуации 1, 2 не имеют места, то имеет место ситуация 3, при которой можно перейти в новую вершину допустимого множествазадачи (3.11), более близкую к оптимальной. Начинается этот переход с определения r -номера направляющей строки таблицы, задающего номер S_r- вектора условий A_Sr, выводимого из базиса F_SПри выбореrможно реализовать два метода.

Таблица 3.35 Таблица двойственного симплекс-метода

				С1	...	Сk	...	Сn
№	СS	FS	A0	A1	...	Ak	...	An
1	СS1	AS1	x10	x11	...	x1k	...	x1n
...	...	...	...	...	...	...	...	...
r	СSr	ASr	xr0	xr1	...	xrk	...	xrn
...	...	...	...	...	...	...	...	...
m	СSm	AS1	xm0	xm1	...	amk	...	amn
m+1			Z0		...		...
m+2						

Точный метод.В качестве направляющей строки выбирают ту, на которой достигается наибольшее убывание:

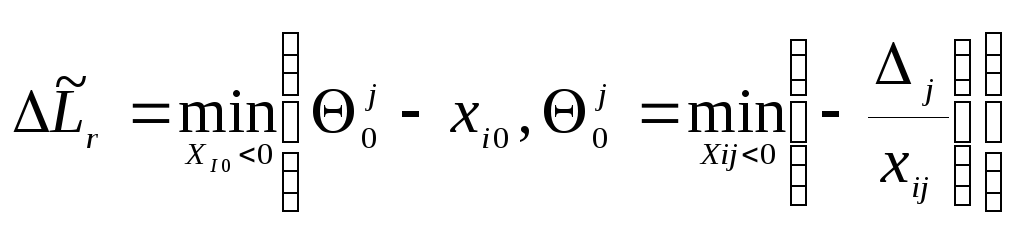
Приближенный метод.В качестве направляющей строки выбирают ту, которой соответствует наименьшая базисная компонента псевдоплана

Для определения k - номера направляющего столбца таблицы, задающего номер вектора условий, который должен войти в базис новой вершины. двойственной задачи (3.11), вычисляютнаходят все номера j столбцов таблицы, для которых достигаетсяЕслидостигается на одном столбце таблицы, то он и является направляющим столбцом таблицы. Еслидостигается на нескольких столбцах, то в качестве направляющего берут тот, которому соответствует вектор условий с наименьшим порядковым номером.

После определения номеров kиrстроят базиснового опорного планазаменой ввектора условийнаи формируют новый столбец С_Sзаменой С_Srна С_kостальные элементы столбцов F_Sи С_Sтаблицам остаются прежними.

Элементы таблицы, соответствующей базису пересчитывают по формулам (3.4) и принимают вновь полученную симплекс-таблицу в качестве исходной и повторяют описанный выше процесс. Общая схема метода последовательного уточнения оценок (первый алгоритм) приведена на рис. 3.4. Рассмотрим вычислительный пример, иллюстрирующий порядок действий по первому алгоритму.

Пример 3.9.

Решить задачу ЛП

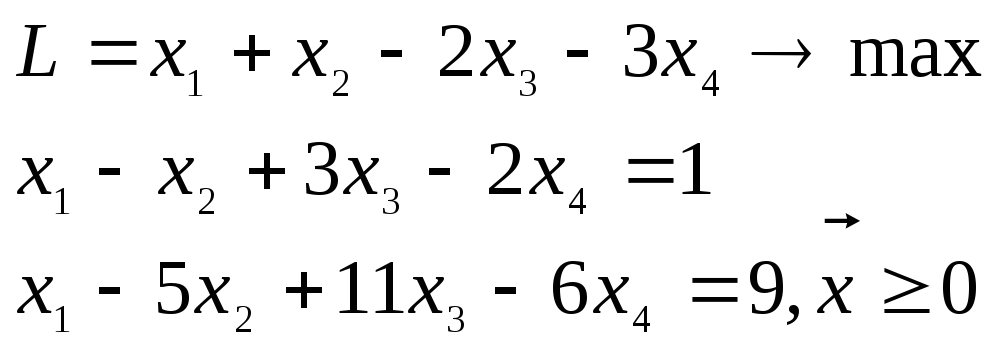
двойственным симплекс-методом (первый алгоритм), взяв в качестве исходного опорный план двойственной задачи с базисом. Для заполнения исходной таблицы вычислим матрицу, обратную к

По формуле находим матрицу коэффициентов разложений векторов условийи вектора ограниченийпо базису F_s .

Параметры определяют по формулам

С учетом выполненных вычислений начальная таблица (табл. 3.36 ) меняет свойвид.Движение в оптимальную вершинуначинают с анализа ситуаций

Имеет место ситуация 3. С помощью приближенного метода определяют r, равное 1/2, достигается при k=3. Новый опорный планимеет базис. Соответствующая ему таблица (табл. 3.37) пересчитывается по формулам (3.4).

Таблица 3.36 Начальная таблица

			С	1	1	-2	-3
№	СS	FS	A0	A1	A2	A3	A4
1	1	A1	-1	1	0	1	-1
2	1	A2	-2	0	1	-2	1
3			-3	0	0	1	3
4						1/2

Таблица 3.37 Начальная таблица

			С	1	1	-2	-3
№	СS	FS	A0	A1	A2	A3	A4
1	-1	A1	-2	1	1/2	0	-1/2
2	-2	A3	1	0	-1/2	1	-1/2
3			-4	0	1/2	0	7/2
4							7

Из анализа ситуаций для полученной таблицы

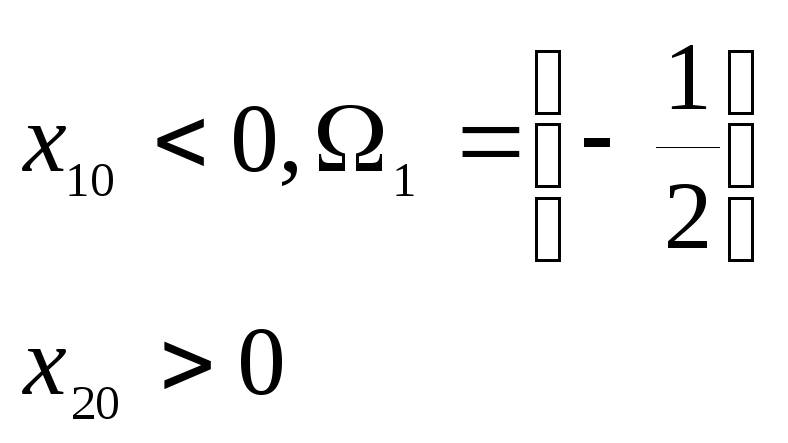
следует, что имеет место ситуация 3. r=1,k=4 Базис нового опорного плана -Симплекс таблица новой вершины двойственной задачи (табл. 3.38) имеет вид:

Таблица 3.38 Конечная таблица

№	СS	FS	A0	A1	A2	A3	A4
1	-3	A4	4	-2	-1	0	1
2	-2	A3	3	-1	-1	1	0
3			-18	-7	4	0	0

Из анализа ситуаций для вновь полученной таблицы следует, что и имеет место ситуация 1. Оптимальный базис, значениезадачи равно - 18.

3.6. Метод последовательного уточнения оценок (второй алгоритм)

Для решения задачи ЛП данным методом ее необходимо представить в канонической форме (3.1) и задать начальный опорный план двойственной к ней задаче (3.11) с базисом. Если в первом алгоритме параметрывычисляются по формулам (3.5), то основой второго алгоритма являются другие формулы

(3.12)

совпадающие с формулами (3.6) при . Второй алгоритм двойственного симплекс метода решения задач (3.1), (3.11) начинаются с заполнения вспомогательной и основной таблиц. Вспомогательная таблица (табл. 3.39) содержит информацию о задаче (3.1) и имеет вид:

Таблица 3.39 Вспомогательная таблица

№	b	A1	...	Ak	...	An
1	b1	a11	...	a1k	...	a1n
...	...	...	...	...	...	...
m	bm	am1	...	amk	...	amn
m+1		С1	...	Сk	...	Сn
m+2			...		...
m+3			...		...
m+4				

Основная таблица содержит переменную информацию, определяемую базисами опорных планов задачи (3.11), перебираемых в процессе движения к оптимальному плану , (табл. 3.40) и имеет вид:

Здесь - элементы обратной матрицы,- базисные компоненты псевдоплана, параметры.

Таблица 3.40 Основная таблица

№	С	FS	e0	e1	...	em	Ak
1	CS1	AS1	e10	e11	...	e1m	x1k
...	...	...	...	...	...	...	...
r	CSr	ASr	er1	er2	...	erm	xrk
...	...	...	...	...	...	...	...
m	CSm	ASm	em1	em2	...	emm	xmk
m+1					...

Движение в оптимальную вершину (переход от исходной таблицы к последующей) начинают с вычисления параметровпо формулам (3.12) и установления наличия ситуации 1().

Если среди базисных компонент псевдоплана есть отрицательные, то находят номер направляющей строки, используя точный или приближенный метод. Знаяr, заполняют направляющую. строкувспомогательной таблицы:, где-r-я строка матрицыЕсли, то имеет место ситуация 2. В противном случай находят значение

и определяют столбцы таблицы, на которых достигается . Еслидостигается на нескольких столбцах таблицы, то в качестве направляющего берут тот, которому соответствует вектор условий с наименьшим порядковым номером. Зная k , заполняют направляющий столбец A_kосновной таблицы, занося в m+1 строку значение, а в остальные строки элементы вектора.

После определения номеров k и r формируют базис нового опорного планазадачи (З.11) путем замены вектора условийнаОдновременно формируют новый столбец C_Sтаблицы заменой C_Srна C_K, остальные элементы столбцов F_Sи C_Sостаются прежними.

Элементы новой таблицы вычисляют по формулам:

,

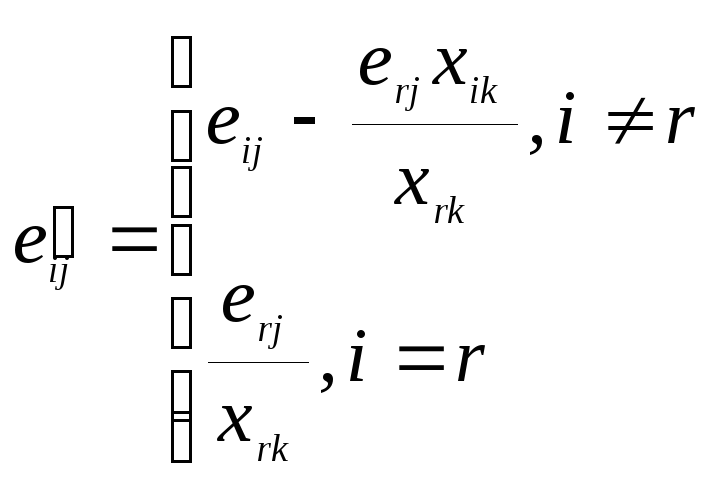где I= 1,2,...,m+1,j= 0,1,2,...,n. Вновь полученную основную таблицу, соответствующую , берут в качестве исходной, и описанный процесс повторяется. Общая схема метода последовательного уточнения оценок (второй алгоритм) приведена на рис. 3.5. Рассмотрим вычислительный пример, иллюстрирующий порядок действий по второму алгоритму.

Пример 3.10.

Решить задачу ЛП:

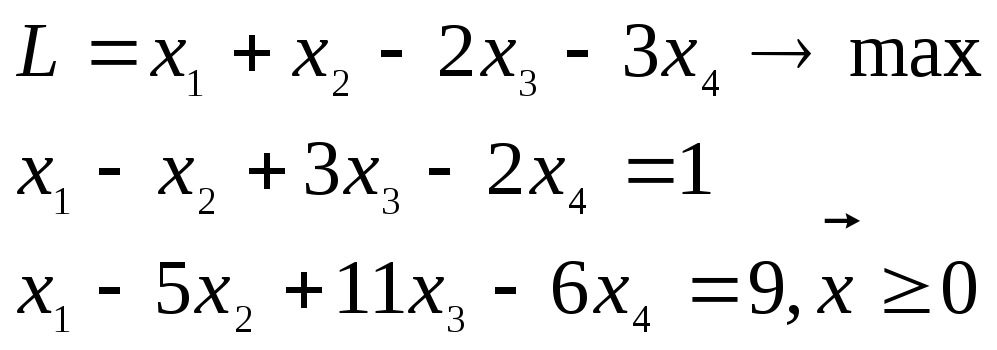
двойственным симплекс-методом (второй алгоритм), взяв в качестве исходного опорный план двойственной задачи с базисом. Вспомогательная таблица (табл. 3.41) имеет вид:

Таблица 3.41 Вспомогательная таблица

№	b	A1	A2	A3	A4
1	1	1	-1	3	-2
2	9	1	-5	11	-6
3	С	1	1	-2	-3
4		0	1/2	0	7/2
5		1	1/2	0	-1/2
6					7

Для заполнения основной таблицы вычислим , обратную к:

Базисные компоненты псевдоплана Параметрынаходят по формулам

.

С учетом выполненных вычислений основная таблица (табл. 3.42) имеет следующий вид.

Вычислив и занеся их в четвертую строку вспомогательной таблицы, анализируют ситуации:. Так как единственная базисная компонента псевдоплана отрицательна, то r=1. Находят элементы

Таблица 3.42 Основная таблица

№	С	FS	e0	e1	e2	A4
1	1	A1	-2	11/8	-3/8	-1/2
2	-2	A3		-1/8	1/8	-1/2
3			-4	13/8	-5/8	7/2

направляющей строки .Множествопоэтому определяют. В третью строку столбца таблицызаносят, в остальные строки - компоненты вектора. Для k=4, r=1 строят базиснового опорного планадля которого заполняют основную таблицу (табл. 3.43).

Так как то имеет место ситуация 1. Оптимальный базис,, значениезадачи равно -18.

Таблица 3.43 Основная таблица

№	С	FS	e0	e1	e2
1	-3	A4	4	-11/4	3/4
2	-2	A3		-6/4	2/4
3			-18	45/4	-13/4

3.7. Определение начального опорного плана в двойственном симплекс-методе

Решение задачи линейного программирования методом последовательного уточнения оценок начинается с известного базиса опорного плана двойственной задачи. Иногда задача позволяет без труда указать исходный опорный план , а следовательно, и исходный базис. Существуют задачи для которыхможет быть определен достаточно легко. Так значительное их число об оптимальных смесях описываются задачами ЛП следующего вида:

Записав задачу в канонической форме:

где - вектор искусственных переменных, введенных на этапе канонизации,- единичная матрица размером mm , строят двойственную к ней задачу. Векторявляется опорным планом этой задачи с базисомгде. Указанный базис и берут в качестве исходного при решении задачи методом последовательного уточнения оценок (1, 2 алгоритм).

Пример 3.11.

Пусть задача ЛП имеет вид:

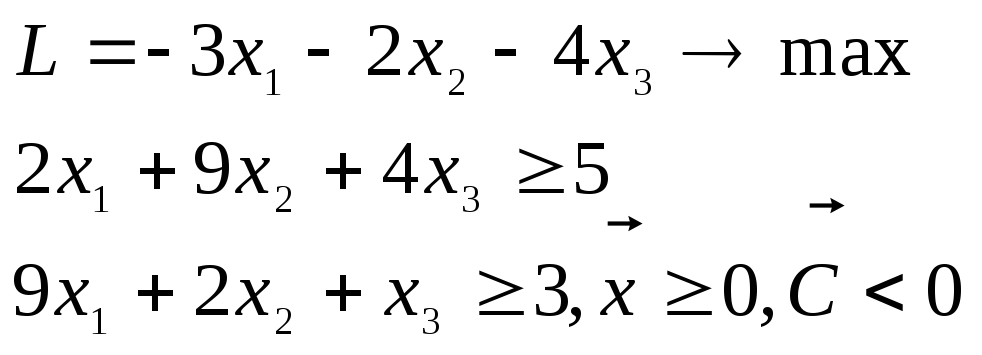
Записав задачу в канонической форме:

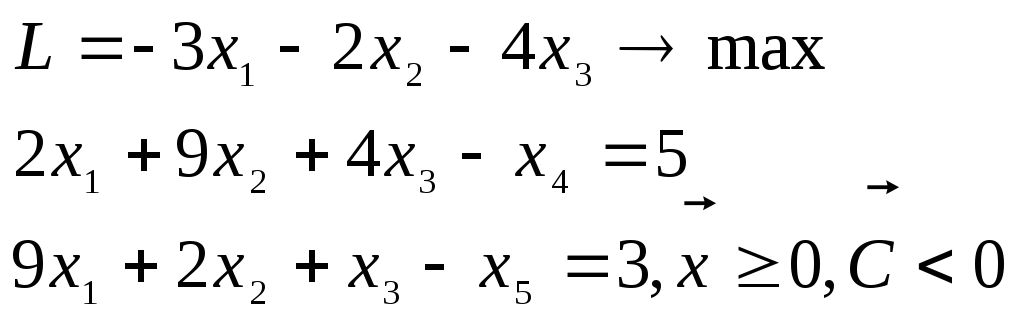
и построив двойственную к ней задачу:

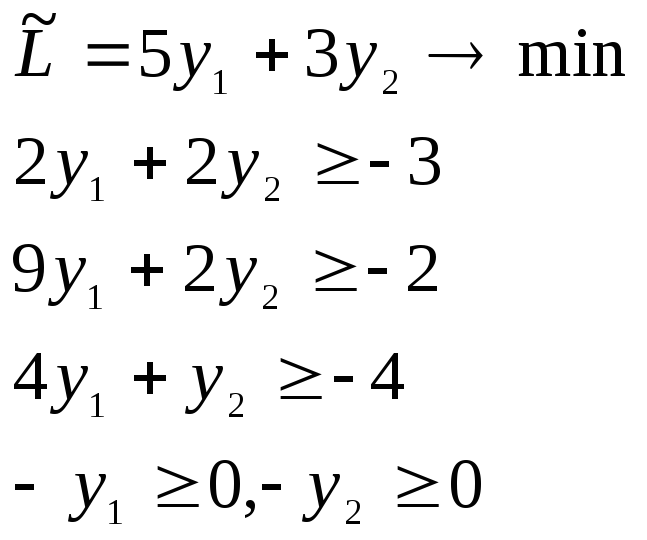
получают, что с базисомявляется опорным планом двойственной задачи.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Перечислите конечные методы решения задач линейного программирования.

2. Из каких этапов складывается общая схема конечных методов?

3. Сформулируйте признак оптимальности метода последовательного улучшения плана.

4. Укажите структуру и сущность анализа симплекс-таблицы.

5. Особенности методов выбора номера направляющего столбца симплекс-таблицы.

6. 1. Особенности выбора номера направляющей строки симплекс-таблицы.

   Как осуществляется формирование базиса новой вершины в симплекс-методе?

7. Укажите особенности пересчета элементов симплекс-таблицы.

8. Перечислите основные этапы преобразования информации при переходе к новому опорному плану в симплекс-методе.

9. Укажите структуру вспомогательной и основной таблиц в методе обратной матрицы.

10. Как проверяется разрешимость задачи в методе обратной матрицы.

11. Укажите особенности пересчета основной таблицы при переходе к новому опорному плану.

12. Перечислите основные этапы преобразования информации при переходе к новому опорному плану в методе обратной матрицы.

13. В чем сущность проблемы выбора начального опорного плана?

14. Из каких этапов складывается метод искусственного базиса?

15. Укажите свойства вспомогательной задачи метода искусственного базиса.

16. Как строится М - задача?

17. Основные свойства М - задачи?

18. Укажите структуру симплекс-таблицы в М - методе.

19. Какая структура основной и вспомогательной таблицы М - методе?

20. Укажите правила построения и свойства псевдоплана прямой задачи.

21. Укажите структуру симплекс-таблицы двойственного симплекс-метода,

22. В чем состоит анализ симплекс-таблицы двойственного симплекс-метода?

23. Укажите структуру таблиц двойственного симплекс-метода.

24. Перечислите основные этапы преобразования информации при переходе к новому опорному плану в двойственном симплекс-методе.

25. Чем вызвано наличие разнообразных методов и схем решения задач линейного программирования?