1.2. Типовые содержательные задачи лп, являющиеся задачами исследования операций

1.2.1. Задача определения оптимального ассортимента товарной продукции машиностроительного завода. Оперирующей стороной является машиностроительное предприятие, способное производить nвидов товарной продукции объемомX_j,каждый. На рынке каждойj-й товарной продукции имеет место конкуренция производителей (предложение опережает спрос), и складываются ценыCjна единицу товара.

Для производства каждого вида товарной продукции расходуются активные средства, представляющие собой производственные факторы предприятия, такие как трудовые ресурсы, оборудование, энергия, материалы, транспорт, производственные мощности, площади, оборотные средства и т.п. Всего mвидов ресурсов. Объем каждогоi-го ресурса составляетb_iединиц измерения,. Процесс производства полагается линейным. Следовательно,b_ij- затратыi-го ресурса на производствоj-й товарной продукции прямо пропорциональны объему выпускаX_j : b_ij=a_ijX_j, гдеa_ij- постоянный коэффициент пропорциональности, характеризующий затратыi-го активного средства на производство единицыj-й товарной продукции. Система неравенств

a_i1x₁+a_i2x₂+...+a_inx_n<b_i,

отражает условия ограниченности расходуемых объемов производственных факторов. Условия неотрицательности

исключают приток товарной продукции извне.

На часть товарной продукции предприятия существует госзаказ, определяемый вектором

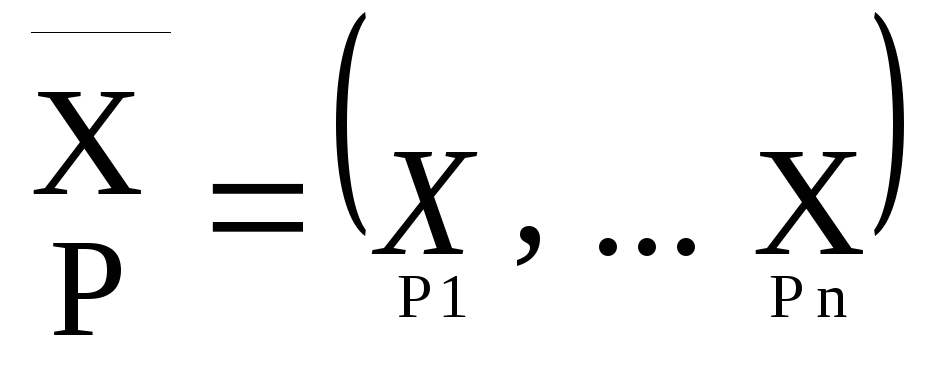
Вектор определяет договорные цены на единицу товарной продукции по госзаказу. В рассматриваемом случае операция представляет собой организацию производства сверхплановой товарной продукции, продажа которой на рынке обеспечит максимальные доходы предприятия.

Математическая модель операции представляет собой задачу ЛП:

при ограничениях

a₁₁x₁+a₁₂x₂+...+a_1nx_n<b₁

a₂₁x₁+a₂₂x₂+...+a_2nx_n<b₂

— — — —— —— ——

a_m1x₁+a_m2x₂+...+a_m1nx_n<b_m

X­> X_j (1.8)

Основная задача исследования операции состоит в определении решения задачи (1.8) - вектора оптимальных объемов производства товарной продукции. Искусственные, отличные от нуля переменныеX_­­­*_n+i, введенные на этапе приведения задачи (1.8) к канонической форме, характеризуют излишки активных средств в

оптимальном случае, определяют резервы производства машиностроительного предприятия. Векторы условий оптимального базисаопределяют множество номеров видовтоварной продукции, которые выгодно производить при сложившейся системе цен на рынках.

Оптимальное значение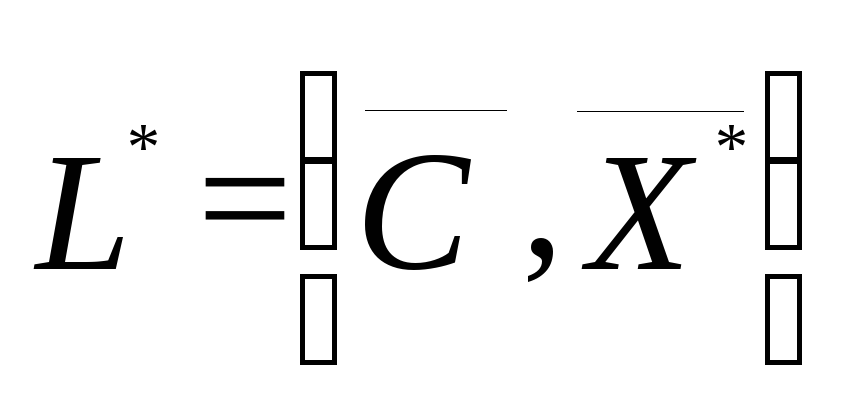целевой функции определяет

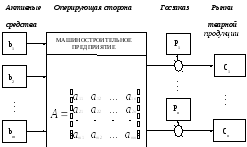
Рисунок 1.1. Структурно-функциональная схема операции

доход предприятия при продаже всей произведенной продукции по рыночным ценам. Доход от продажи сверхплановой продукции определяется формулой

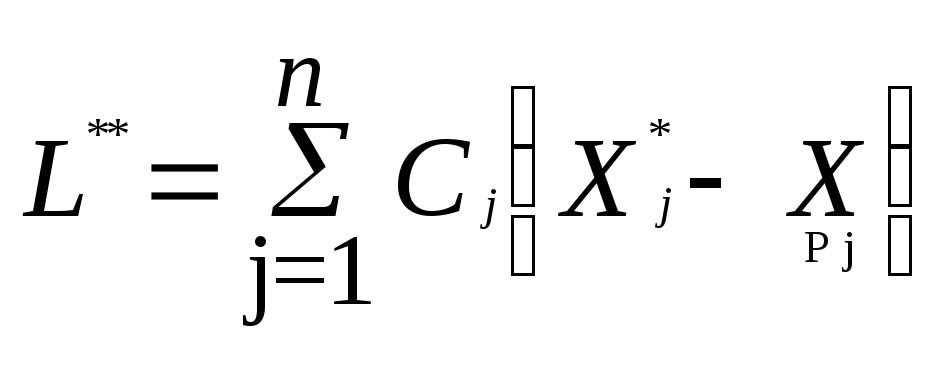
Неотрицательный вектор двойственных переменных определяет ценности единиц активных средств оперирующей стороныи ценности единиц товарной продукции по госзаказу

Задача, двойственная к (1.8)

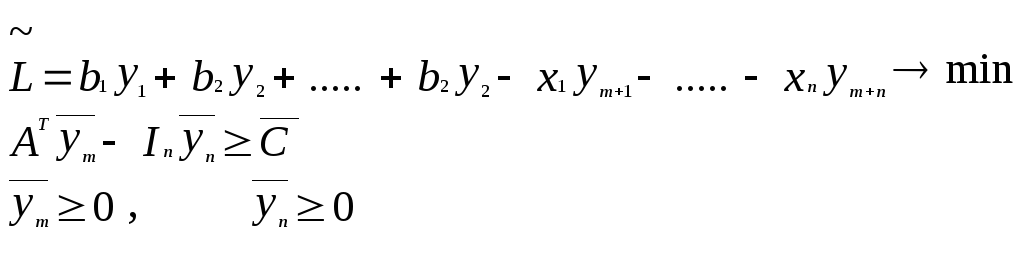
где,

представляет собой задачу объективного оценивания имеющихся активных средств и производимых видов товарной продукции в условиях превышения затрачиваемых ценностей над производимыми.

Оптимальный вектор ; характеризует объективные оценки единиц активных средств предприятия,- объективные оценки единиц производимой товарной продукции.

1.2.2. Задача оптимального использования ресурсов информационно-вычислительного центра. Оперирующей стороной является информационно-вычислительный центр (ИВЦ), способный осуществлять работы n- видов, объемомX_j каждый, .На рынкеjкаждой работыX_jимеет место конкуренция производителей работ и складываются ценыC_jна единицу измерения работы.

Для производства каждого вида работ расходуются активные средства ИВЦ (трудовые ресурсы, вычислительные средства, энергия, носители информации, бумага и т.д.). Всего рассматривается mвидов ресурсов. Объем каждогоi-гoресурса составляетb_i­; единиц измерения,. Процесс производства полагается линейным.

Следовательно, b_ij­ - затратыi-го ресурса ИВЦ на производствоj-го вида работ - прямо пропорциональны объему работыX_j b_ij=a_ijX_j, гдеa_ij- постоянный коэффициент пропорциональности, определяющий затратыi-го активного средства на производство единицыj-й работы. Система неравенствa_i1x₁+a_i2x₂+...+a_inx_n<b_i, отражает условия ограниченности используемых объемов активных средств ИВЦ.

Условия неотрицательности исключают возможность фиктивных работ. В рассматриваемом случае операция представляет собой организацию производства таких работ, которые при сложившейся системе цен на рынках обеспечат максимальные доходы ИВЦ.

Математическая модель операции представляет собой задачу ЛП в стандартной форме записи

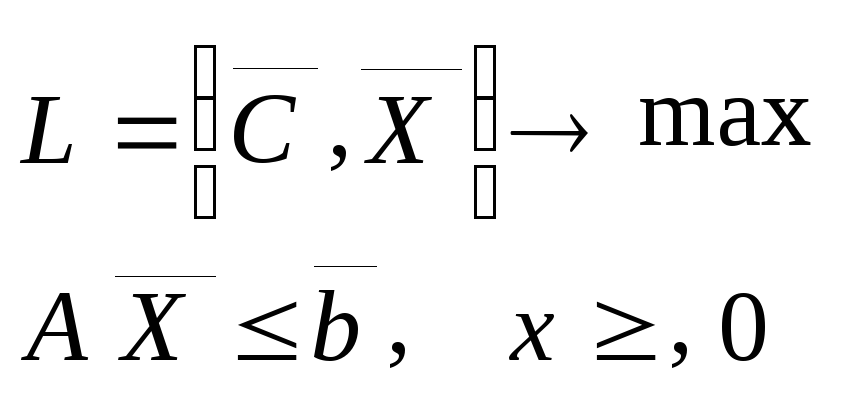(1.9)

Основная задача исследования операции состоит в определении решения задачи (1.9) - вектора оптимальных объемов производимых работ. Отличные от нуля искусственные переменныеX*_n+i, введенные на этапе приведения задачи (1.9) к канонической форме, определяют резервы ИВЦ.

Рисунок 1.2. Структурно-функциональная схема операции

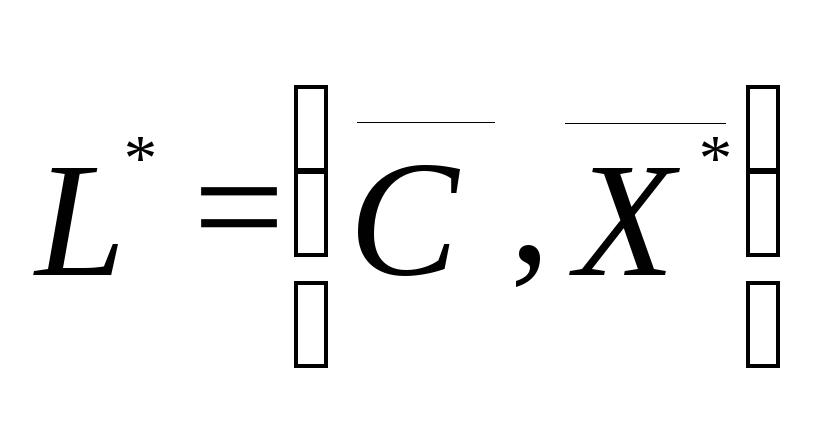Оптимальный базис задает множествономеров видов работ, которые выгодно производить ИВЦ. Оптимальное значение целевой функции определяет максимальный доход ИВЦ, который он может получить при имеющихся объемах активных средств.

Неотрицательный вектор двойственных переменных определяет ценности единиц активных средств ИВЦ.

Задача, двойственная к (1.9):

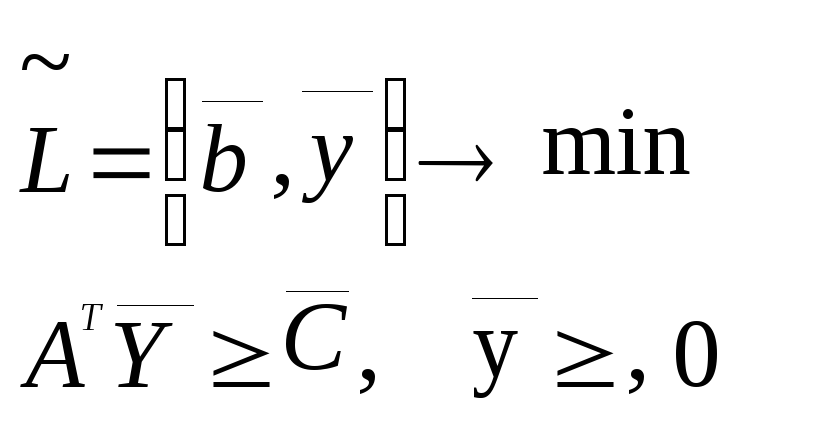(1.10)

является задачей объективного оценивания ресурсов ИВЦ в условиях превышения затрачиваемых ценностей над произведенными Оптимальный план задачи (1.10) задает объективные ценности единиц активных средств оперирующей стороны.

1.2.3. Задача оптимальной закупки вычислительных средств информационно-вычислительным центром. Оперирующей стороной является администрация ИВЦ, решающая проблему закупки ЭВМ, обеспечивающих в ближайшем году максимальную прибыль, от их эксплуатации. Для каждого вида jЭВМ наj-м рынке имеет место конкуренция производителей вычислительной техники и складывается ценаp_j,.Для приобретения ЭВМ ИВЦ располагает финансовыми средствами объемомФ, производственной площадьюS, трудовыми ресурсамиT и другими активными средствами общей численностьюmвидов. При этомb₁= Ф ,b₂= S , b₃= Tи т.д. Затраты активного средства ИВЦ на одно приобретаемое вычислительное средствоjопределяются элементамиa_ij матрицыA,, При этомa_1j= p_j, ,a_2j- площадь, необходимая для приобретаемой ЭВМ,a_3j- объем трудовых ресурсов, необходимый для обслуживания приобретаемой ЭВМ. Если - вектор, определяющий объемы закупок вычислительных средств, то система неравенствотражает ограниченность объемов располагаемых активных средств ИВЦ. Условия неотрицательности исключают другие источники приобретения ЭВМ, кроме имеющихся рынков.

Прибыль C_jот эксплуатации в ближайшем году приобретенной ЭВМ определяется разностьюC_j=d_j-r_j доходовd_j от эксплуатации и расходовr_jна обслуживание одного вычислительного средстваj-то вида, .

В рассматриваемом случае операция представляет собой закупку вычислительных средств, обеспечивающих максимальную прибыль от их эксплуатации.

Математическая модель операции представляет собой задачу ЛП вида (1.9). Основная задача исследования операции состоит в определении решения задачи (1.9), определяющего оптимальные объемы закупаемых вычислительных средств. Отличные от нуля искусственные переменныеX^*_n+i , введенные на этапе приведения задачи (1.9) к канонической форме, определяют резервы ИВЦ. Оптимальный базисзадает множество номеров типов ЭВМ, которые выгодно приобретать ИВЦ. Оптимальное значение 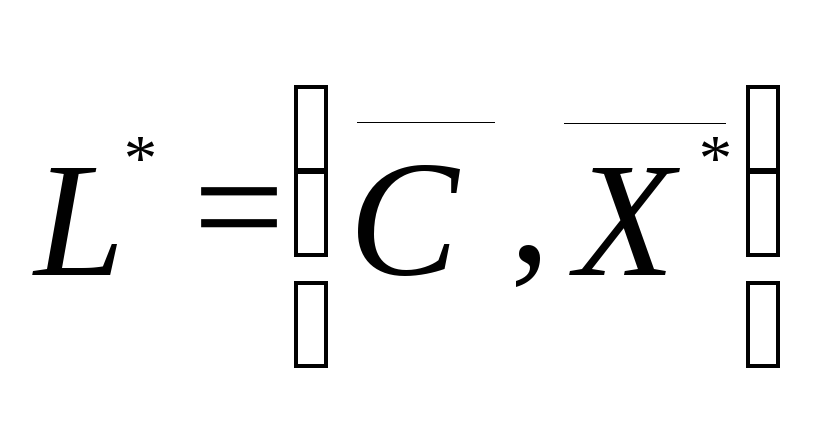определяет максимальную прибыль ИВЦ от приобретения дополнительных вычислительных средств в условиях ограниченности объемов имеющихся активных средств.

Двойственная задача (1.10) к задаче (1.9) является задачей объективного оценивания активных средств, выделяемых для приобретения дополнительных вычислительных средств в условиях превышения затрат над прибылью. Оптимальный планзадачи (1.10) задает

Рисунок 1.3. Структурно-функциональная схема операции

объективные ценности единиц выделенных ИВЦ резервов активных средств.

1.2.4. Задача о дешевой диете (о дешевом рационе питания). Оперирующей стороной является пункт питания, обеспечивающий минимальные потребности обслуживаемого контингента населения в питательных веществах, микроэлементах и других жизненно необходимых компонентах при минимальных затратах. Пищевые продукты j, ,содержащие питательные вещества и витамины необходимых видов, ежедневно приобретаются в объемеX_jнаj-м рынке продуктов, где имеет место конкуренция производителей и складывается некоторая ценаC_jна его единицу. Диета характеризуется вектором суточных потребленийX_jпищевых продуктовj,с каждой диетой связывается соответствующее ей количество питательных веществ и микроэлементов - белков, жиров, углеводов, клетчатки, железа, кальция, витаминов и других жизненно необходимых компонент. Обозначая минимальную ежесуточную потребность организма вi-м питательном веществе черезb_i, а содержаниеi- го питательного вещества в единицеj-го продукта черезa_ij,(, )получаем, что система неравенствa_i1x₁+a_i2x₂+...+a_inx_n<b_{i ,} отражает требования удовлетворения диетой минимальных ежесуточных потребностей организма во всехmпитательных веществах.

Условия неотрицательности исключают другие источники приобретения пищевых продуктов, кроме рынков.

В рассматриваемом случае операция представляет собой организацию производства таких диет, которые при сложившихся ценах на продукты обеспечат потребности населения при минимальных затратах.

Математическая модель операции представляет собой задачу ЛП

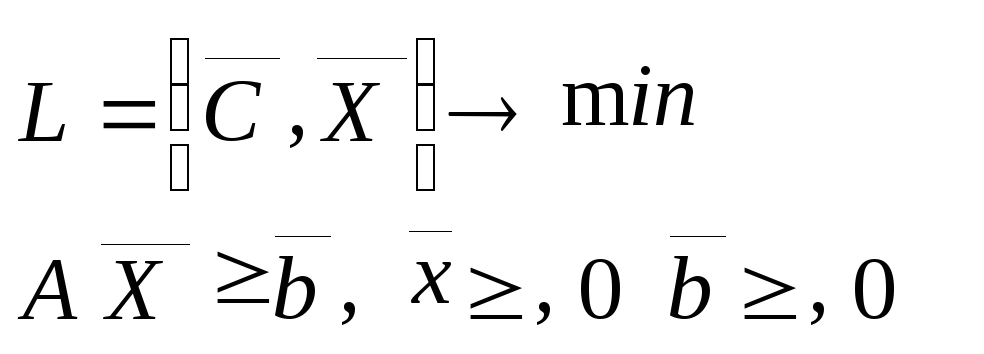(1.11)

Основная задача исследования операции состоит в определении решения задачи (1.11), задающего оптимальные объемы ежесуточной закупки пищевых продуктов. Отличные от нуля искусственные переменныеX^*_n+i, введенные на этапе приведения задачи (1.11) к канонической форме, определяют излишкиi-то питательного вещества, содержащиеся в оптимальной диете. Оптимальный базисзадает множествономеров пищевых продуктов, которые выгодно закупать на рынках. Оптимальное значениеL^* определяет минимальные затраты на диету.

Двойственная задача

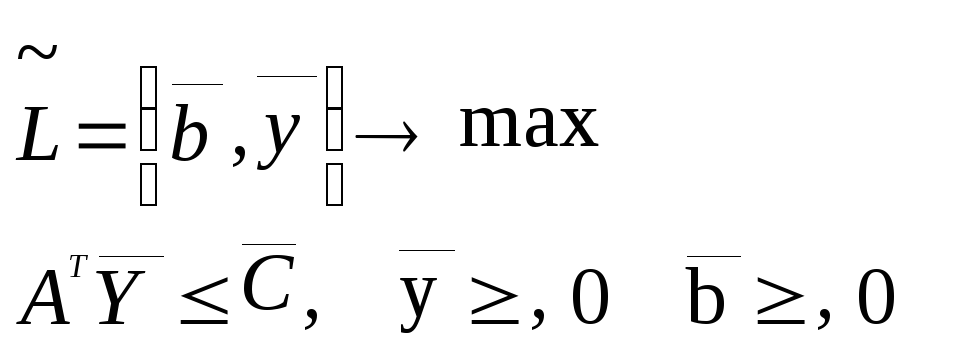(1.12)

к задаче (1.11), представляет собой задачу оптимального оценивания удовлетворения единичных потребностей организма в питательных веществах при условии непревышения суммарной ценности питательных веществ, содержащихся в единице j-го продукта, его рыночной стоимости. Оптимальный план задачи (1.12) задает ценности питательных веществ, содержащихся в диете, при которых суммарная ценность удовлетворяемых диетой минимальных потребностей организма

Рисунок 1.4. Структурно функциональная схема операции

наибольшая.

1.2.5. Задача о дешевой технологической смеси. Оперирующей стороной является пункт изготовления смесей, обеспечивающий ими некоторые технологические процессы. Сырьевые продукты j, , идущие на приготовление смеси, приобретаются в объемеX_jнаj-м рынке продуктов, где имеет место конкуренция производителей продукта и складывается некоторая ценаC_jна его единицу. Смесь характеризуется векторомпотреблений сырьевых продуктов, обеспечивающих необходимоеX_jзаполнение смесителя.

С каждой смесью связывается соответствующее ей количество необходимых для технологического процесса компонент. Обозначая минимально потребное содержание i-го компонента в смеси черезb_i, а содержаниеi-го компонента в единицеj-го сырьевого продукта через a_ij,(, )получаем, что система неравенств

a_i1x₁+a_i2x₂+...+a_inx_n<b_{i ,} отражает требования удовлетворения смесью минимально допустимых потребностей технологического процесса во всехmкомпонентах. Условия неотрицательности исключают другие источники приобретения сырьевых продуктов, кроме рынков.

В рассматриваемом случае операция представляет собой организацию производства таких смесей, которые при сложившихся ценах на сырьевые продукты обеспечат потребности технологического процесса при минимальных затратах.

Mатематическая модель операции представляет собой задачу ЛП (1.11). Основная задача исследования операции состоит в определении решения задачи (1.11), задающего оптимальные объемы закупки сырьевых продуктов для разовой загрузки смесителя. Отличные от нуля искусственные переменныеX^*_n+i , введенные на этапе приведения задачи (1.11) к канонической форме, определяют излишкиi-го компонента, содержащиеся в оптимальной смеси. Оптимальный базисзадает множествономеров сырьевых продуктов, которые выгодно закупать на рынках. Оптимальное значениеL^* определяет

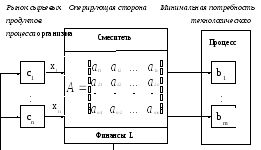
Рисунок 1.5. Структурно функциональная схема операции

минимальные затраты на разовую порцию смеси. Двойственная задача (1.12) является задачей оптимального оценивания удовлетворения единичных потребностей технологического процесса в соответствующих компонентах, при условии непревышения суммарной ценности компонентов, содержащихся в единице j-то продукта, его рыночной стоимостиC_jОптимальный план задачи (1.12) задает ценности единиц компонентов, содержащижея в диете, при которых суммарная ценность удовлетворенных смесью минимальных потребностей технологического процесса наибольшая.

1.2.6. Задача о дешевом станочном парке машиностроительного цеха. Оперирующей стороной является предприниматель, имеющий сбережения (активные средства) и желающий оборудовать станочным парком помещение будущего машиностроительного цеха. Станки типа j, , необходимые для оборудования станочного парка цеха, могут быть приобретены в объемеX_jнаj-м рынке станков, где имеет место конкуренция их производителей и сложилась некоторая ценаC_j.Станочный парк характеризуется вектором приобретенных количествX_j станковj-го типа, обеспечивающих необходимое заполнение помещения цеха. С каждым станочным парком связывается соответствующее ему количество необходимых для выполнения имеющегося заказа машиностроительных работ. Обозначая минимально потребный ежесуточный объем машиностроительных работi-го вида производимых цехом черезb_j, а ежесуточный объем работi-го вида, производимый единицей j-го оборудования черезa_ij получаем, что система неравенствa_i1x₁+a_i2x₂+...+a_inx_n>b_{i ,} отражает требования обеспечения станочным парком ежесуточных минимально допустимых объемов всех видов машиностроительных работ. Условия неотрицательности , исключают другие источники приобретения станков, кроме рынков. В рассматриваемом случае операция представляет собой приобретение станочного парка цеха, который для сложившихся цен на станки обеспечит минимально потребные ежесуточные объемы машиностроительных работ при минимальных затратах.

Математическая модель операции представляет собой задачу ЛП (1.11). Основная задача исследования операции состоит в определении решения задачи (1.11), задающего оптимальные объемы закупки станков для создаваемого машиностроительного цеха.

Отличные от нуля искусственные переменные x^*_n+i, введенные на этапе приведения задачи (1.11) к канонической форме определяют излишки i -го объема работ, выполняемых оптимальным станочным парком. Оптимальный базисзадает множество I_x*={S_1,S_2,...,S _m}номеров типов станков, которые выгодно закупать на

рынках. L^* определяет минимальные затраты на станочный парк.

Двойственная задача (1.12) является задачей оптимального оценивания единичных объемов работ станочного парка при условии непревышения суммарной ценности работ, выполняемых станком j -го типа, его рыночной стоимости C_j. Оптимальный планзадачи (1.12) задает ценности y_iединичных объемов i -х машиностроительных работ, выполняемых цехом, при которых суммарная ценность выполняемых станочным парком ежесуточных минимально потребных работ наибольшая.

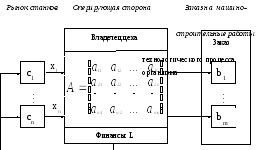
Рисунок 1.6. Структурно-функциональная схема операции

Рассмотренные типовые содержательные задачи ЛП не исчерпывают всех возможных примеров задач исследования операции.

Однако приведенных примеров достаточно для того, чтобы отметить широкий спектр реальных операций, для исследования которых эффективно применение задач и методов ЛП.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Поясните сущность понятий «операция», «состояние», «оперирующая сторона», «цель операции», «активные средства», «стратегия», «факторы операции».

2. Дайте определение критерия эффективности операции, модели операции.

3. Покажите состав математической модели операции.

4. Как классифицируются модели операций?

5. Какими понятиями характеризуются задачи линейного программирования?

6. Сформулируйте постановку задачи определения оптимального ассортимента товарной продукции машиностроительного завода.

7. Сформулируйте постановку задачи оптимального использования ресурсов информационно-вычислительного центра.

8. Сформулируйте постановку задачи оптимальной закупки вычислительных средств.

9. Сформулируйте постановку задачи о дешевой диете, о дешевом рационе питания.

10. Сформулируйте постановку задачи о дешевой технологической смеси.

11. Сформулируйте постановку задачи о дешевом станочном парке машиностроительного цеха.