5.1.1.8. Однородное электрическое поле

Расположим две одинаковые металлические пластины параллельно друг другу на малом расстоянии d. Одной из них сообщим заряд +Q, другой –Q.

При этом полагаем, что заряд Q равномерно распределён по всей площади пластины S.

Поверхностная плотность заряда () – отношение значения заряда к площади поверхности, на которой он распределён.

Однородное поле – поле, напряжённость которого одинакова по модулю и направлению во всех его точках.

• Установлено, что поле между пластинами однородное и его напряжённость .

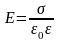5.1.1.9. Работа поля по перемещению заряда

Поместим заряд +q в однородное поле . Со стороны поля на заряд действует электрическая сила , под действием которой он переместился вдоль силовой линии из т.1 в т.2.

Работа поля .

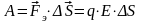Если траектория движения заряда – произвольная кривая, то разделим её на малые участки, считая их прямолинейными. Тогда работа на всём пути , но или , где 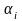– угол между векторами 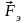и .

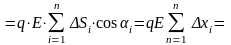
или ,

где x – разность координат конечного и начального положений заряда.

Таким образом, работа поля по перемещению заряда не зависит от траектории, а зависит только от начального и конечного положений заряда.

Работа поля по перемещению заряда из т.1 в т.2: ; из т.2 в т.1: ; по замкнутому контуру: А = А₁₂ + А₂₁ = 0.

Потенциальное поле – поле, работа которого зависит от начального и конечного положений тела и не зависит от его траектории.

• Работа потенциального поля на замкнутом контуре равна нулю.

• Электрическое поле – потенциальное поле.

5.1.1.10. Потенциальная энергия заряда в электрическом поле. Потенциал

Пусть Q и q – точечные положительные заряды, расположенные на расстоянии r друг от друга. Заряд q взаимодействует с полем заряда Q. Значит, q обладает потенциальной энергией Е_П1. Если считать, что в бесконечно удалённой от Q точке _, = 0 (нулевой уровень Е_п), то (с учетом п.1.3.7.4.1) Е_п1 численно равна работе А поля по перемещению q из данной точки в бесконечность:

Согласно принципу суперпозиции полей потенциальная энергия заряда в общем поле нескольких зарядов : (*).

• В практической электротехнике за нуль потенциальной энергии часто принимают потенциальную энергию заряда, находящегося на Земле.

Работа А  q (п.5.1.1.9)  Е_п  q или Е_п = q, где  – коэффициент пропорциональности.

Потенциал () – скалярная физическая величина, численно равная потенциальной энергии единичного точечного положительного заряда, помещённого в данную точку поля (**). 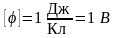– вольт.

•  – энергетическая характеристика точки поля.

• Если поле создано зарядом –Q, то работа А по перемещению заряда +q в бесконечность будет отрицательной (её надо совершить против силовых линий поля) и потенциал данной точки < 0.

• Если поле создано точечным зарядом Q, то на расстоянии r от Q потенциал (***).

(***) справедливо для шара (сферы) радиуса r₀ (несущего заряд Q) на расстоянии r  r₀.

• Для общего поля нескольких зарядов Q_i, из (*) и (**) 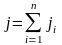 , где _i – потенциал i-того поля в данной точке.

• Сравнивая однородные электрическое и гравитационное поля, видим:

F_т = mg

E_п = mgh

F_э = qE

Е_п = А = qEd

• А = qEd только для однородного поля ( 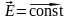) (п.5.1.1.8).