
- •Передмова
- •Методичні вказівки до виконання розрахункових завдань
- •Огляд методів інтегрування.
- •2. Метод інтегрування частинами. Якщо та функції, що мають на деякому проміжку неперервні похідні, то справедлива формула інтегрування частинами:
- •3. Найпростіші інтеграли, які містять у знаменнику
- •4. Інтегрування раціональних дробів.
- •4.1 Розглянемо випадок, коли знаменник розкладається на лише неповторні дійсні множники першого степеня.
- •5.Інтегрування тригонометричних функцій.
- •6.Інтегрування гіперболічних функцій.
- •8.Інтегрування деяких ірраціональних функцій.
- •9.Інтегрування ірраціональних функцій виду
- •Варіанти розрахункових завдань
- •Додаток.
5.Інтегрування тригонометричних функцій.
Інтеграли виду
![]() ,
де
,
де
![]() раціональна функція
двох змінних, приводяться до інтегралів
від раціональної функції нового аргументуtпідстановкою
раціональна функція
двох змінних, приводяться до інтегралів
від раціональної функції нового аргументуtпідстановкою![]() яка називається універсальною. При
цьому використовуються формули
яка називається універсальною. При
цьому використовуються формули![]()
![]() .
.
![]()
Універсальна тригонометрична підстановка,
раціоналізуючи інтеграл
![]() часто приводить до раціональних дробів
з великими степенями. Тому в багатьох
випадках користуються іншими підстановками.
Наведемо деякі з них:
часто приводить до раціональних дробів
з великими степенями. Тому в багатьох
випадках користуються іншими підстановками.
Наведемо деякі з них:
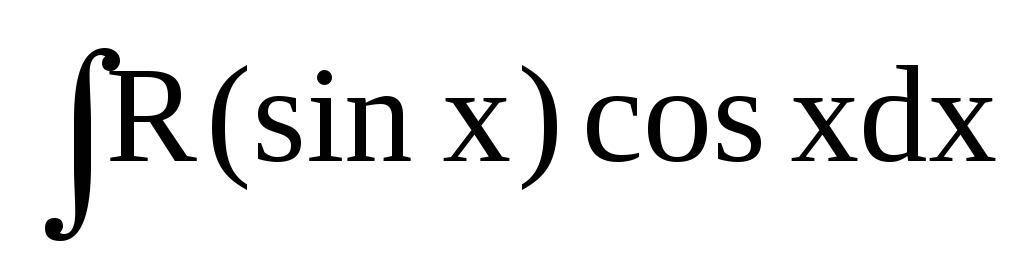 раціоналізується
підстановкою
раціоналізується
підстановкою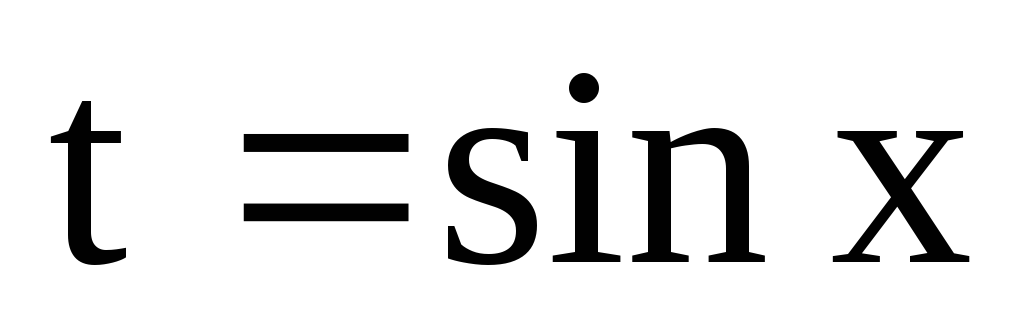 ;
;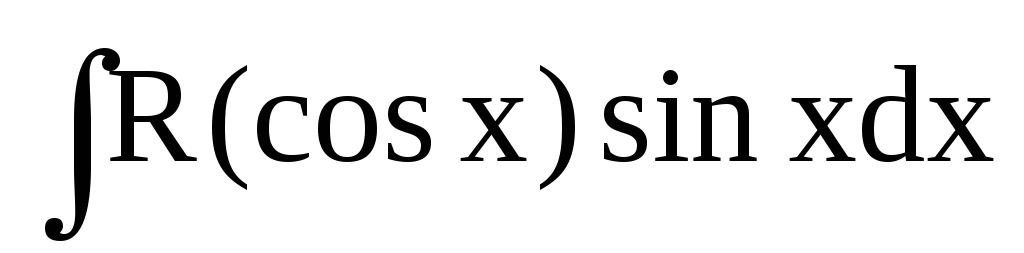 раціоналізується підстановкою
раціоналізується підстановкою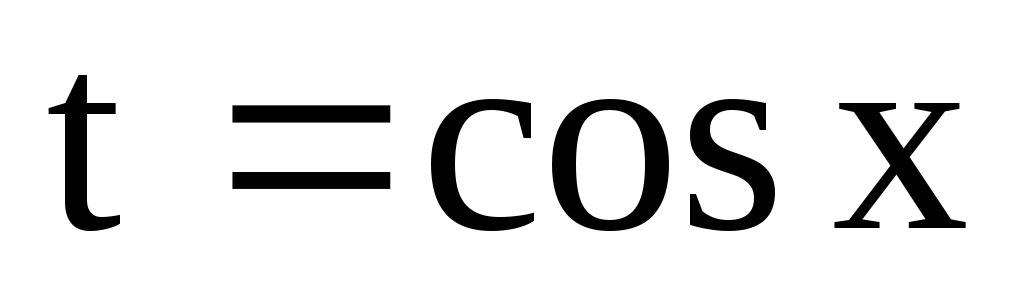 ;
;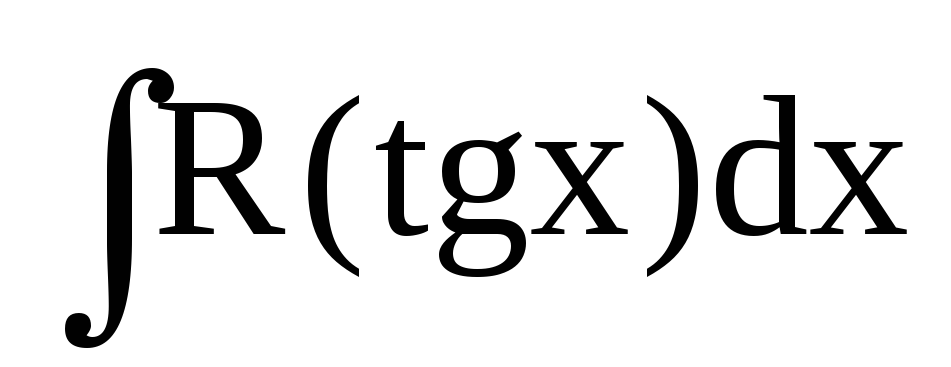 раціоналізується підстановкою
раціоналізується підстановкою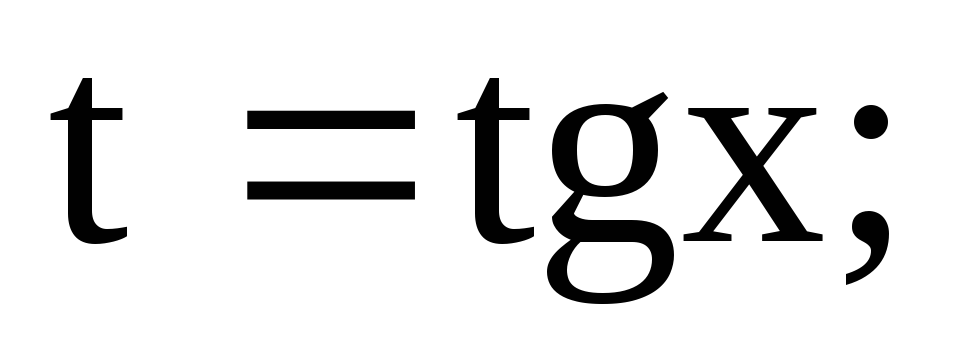
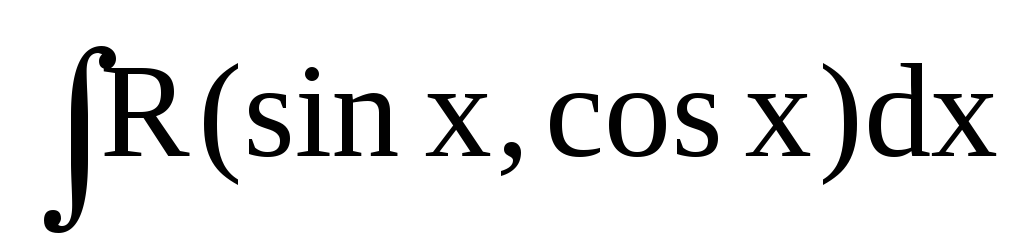
а) якщо функція Rнепарна
відносно![]() ,
,![]()
![]() то функція раціоналізується підстановкою
то функція раціоналізується підстановкою![]()
б) якщо функція Rнепарна
відносно![]() ,
,![]()
![]() то функція раціоналізується підстановкою
то функція раціоналізується підстановкою![]()
в) якщо функція Rпарна
відносно зразу![]() та
та![]() ,
,![]() то
функція раціоналізується підстановкою
то
функція раціоналізується підстановкою![]()
г) якщо функція
![]()
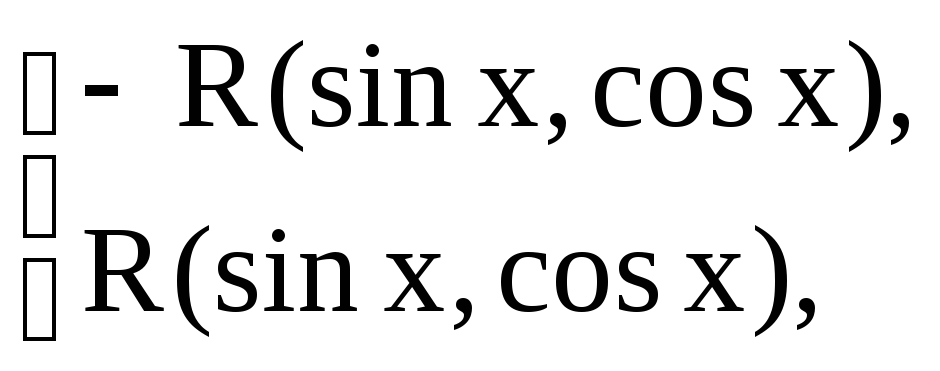 то функція раціоналізується за допомогою
універсальної тригонометричної
підстановки.
то функція раціоналізується за допомогою
універсальної тригонометричної
підстановки.
5)
![]()
а) якщо nціле додатне непарне число, то підстановка![]()
б) якщо mціле додатне непарне число, то підстановка![]()
в) якщо m і nцілі додатні парні числа, то застосовують формули пониження степеня:
![]()
![]()
г) якщо m і n – цілі парні числа, але хоча
б одне з них від’ємне, або коли m і n –
цілі непарні і від’ємні числа, то
використовується підстановка
![]()
інтеграли виду
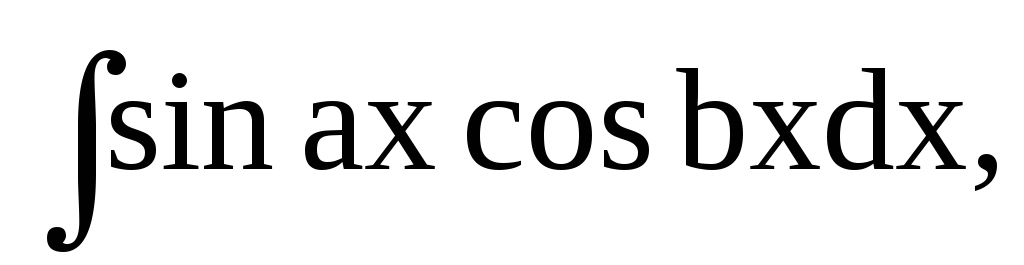
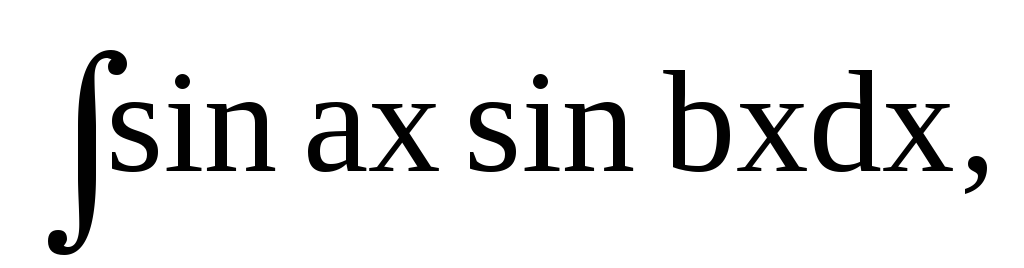
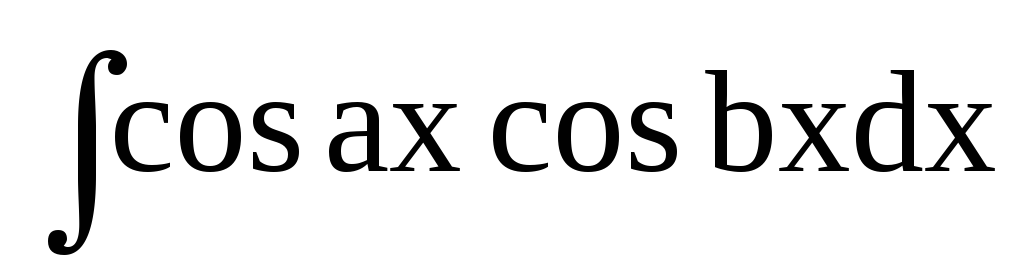 обчислюються
за допомогою тригонометричних формул
перетворення добутку функції в суму:
обчислюються
за допомогою тригонометричних формул
перетворення добутку функції в суму: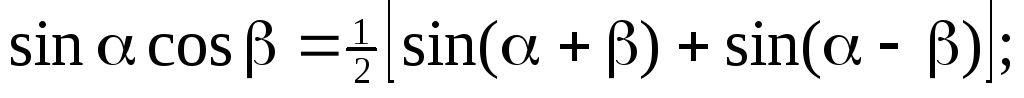
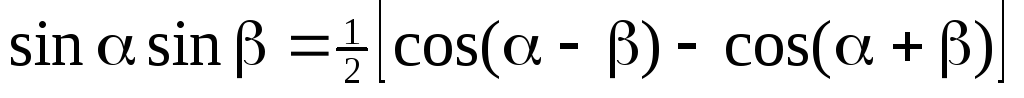 ;
;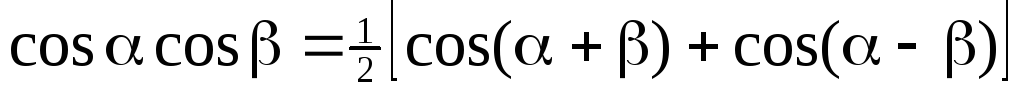 .
.
Приклад 27.
![]() .
.
Рішення. Тут використовується універсальна тригонометрична підстановка.
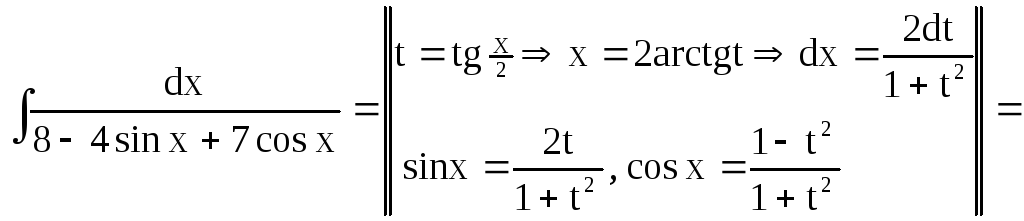
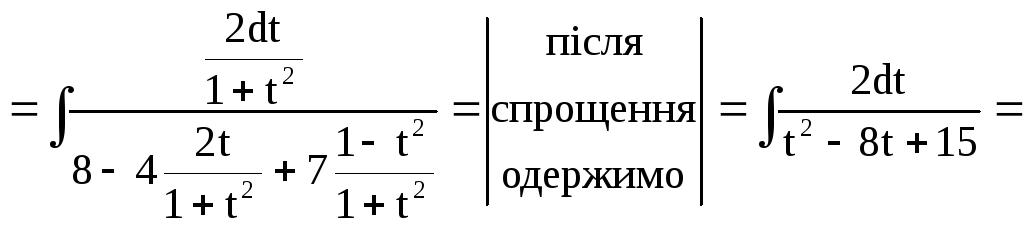
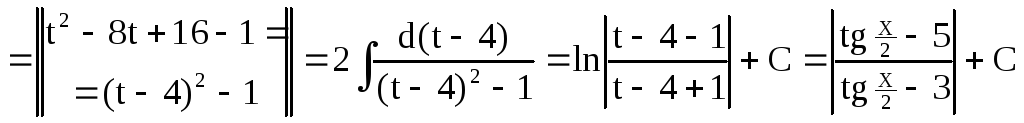 .
.
Приклад 28.
![]() .
.
Рішення. Підінтегральна функція парна
відносно sinxіcosx, тобто![]()
![]() ,
,
використаємо підстановку
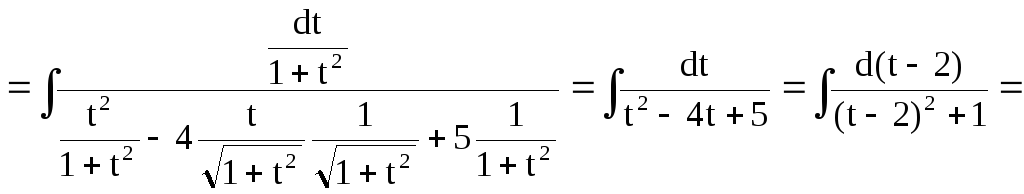
![]() .
.
Приклад 29.
![]() .
.
Рішення. Підінтегральна функція непарна відносно sinx:
![]() використаємо підстановку
використаємо підстановку
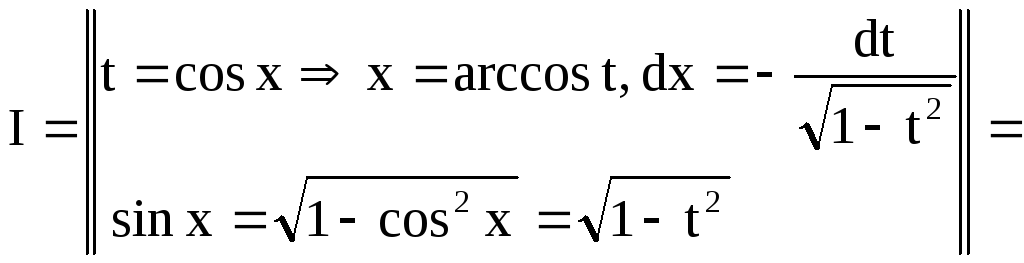
 =
=
![]()
![]()
Приклад 30.
![]()
Рішення.
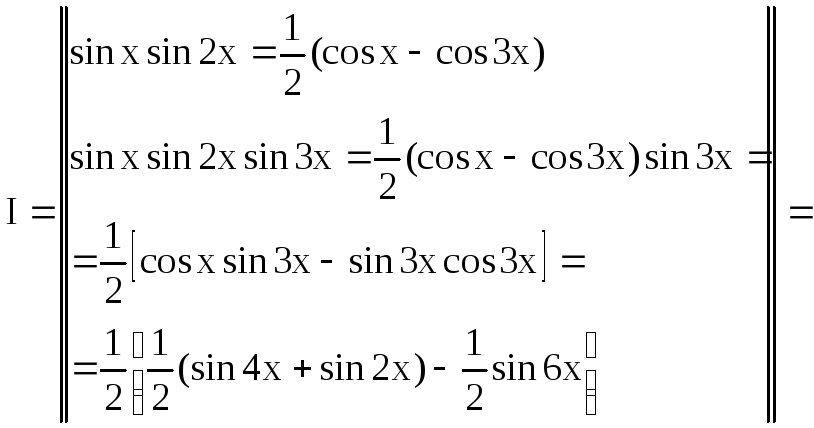
![]()
![]()
Приклад 31.
![]()
Рішення. Цей інтеграл виду
![]() де
де![]() є парне від’ємне число, тому
використаємо підстановку
є парне від’ємне число, тому
використаємо підстановку

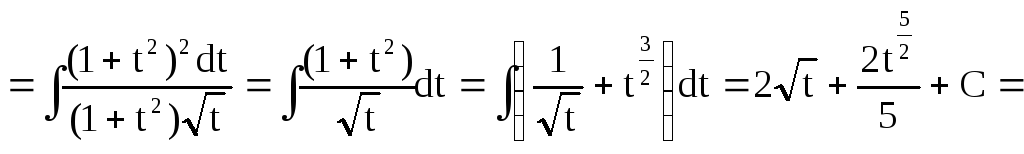
![]()
Приклад 32.
![]()
Рішення. Тут використаємо формули пониження степеня.
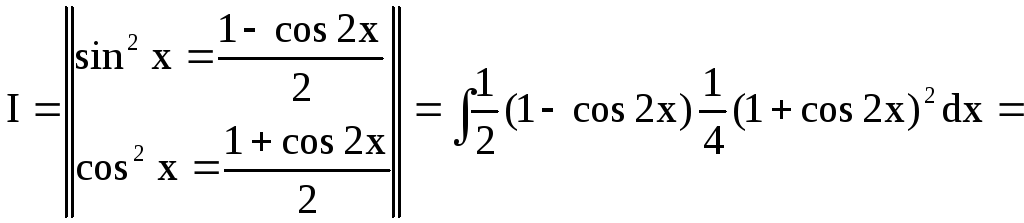
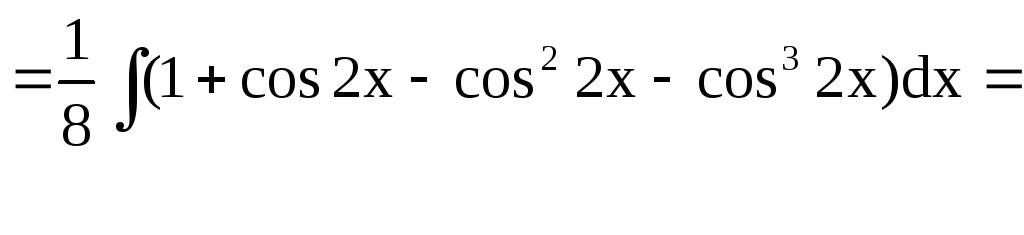
![]()
![]()
![]()
![]()
Приклад 33.
![]()
Рішення. Цей інтеграл можна обчислити двома способами.
Перший спосіб – застосування формули пониження степеня.
![]()
![]()
![]()
![]()
![]()
Другий спосіб– застосування рекурентної формули
![]() тоді
тоді
![]()
![]()
![]()
![]()
6.Інтегрування гіперболічних функцій.
Інтегрування гіперболічних функцій
![]() виконується аналогічно інтегруванню
тригонометричних функцій. При цьому
використовуються такі формули:
виконується аналогічно інтегруванню
тригонометричних функцій. При цьому
використовуються такі формули:
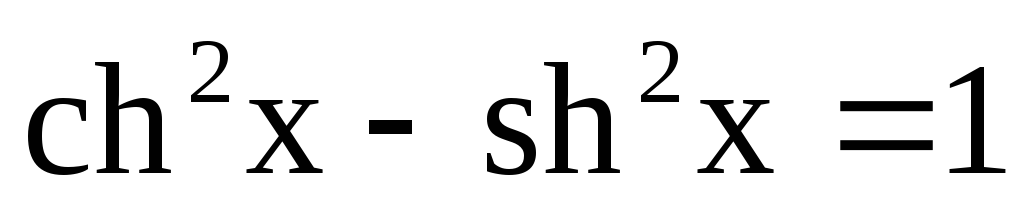
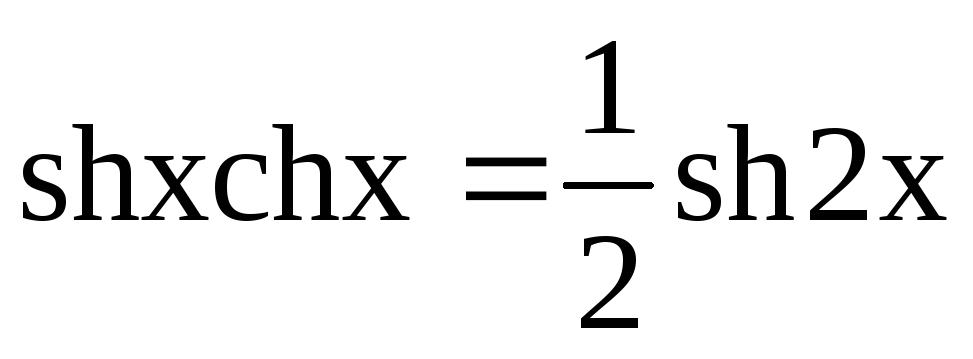
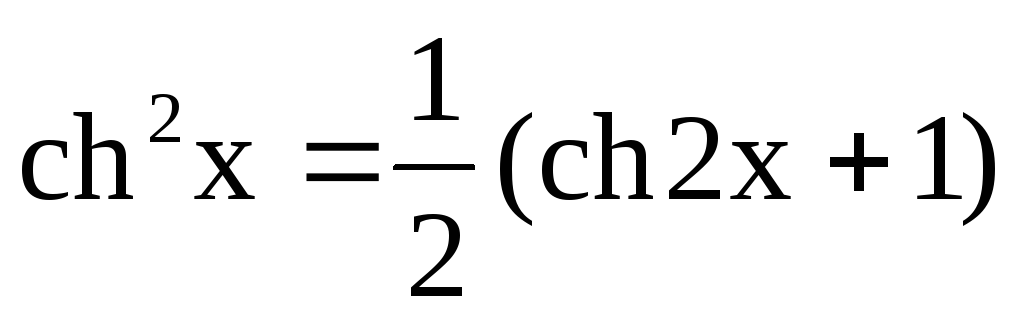
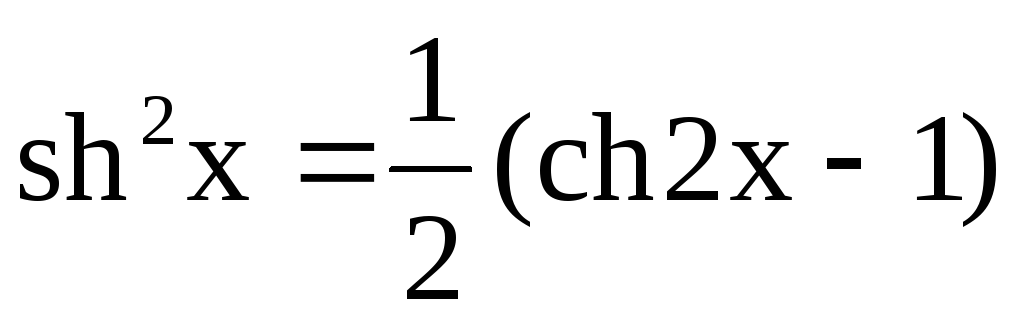
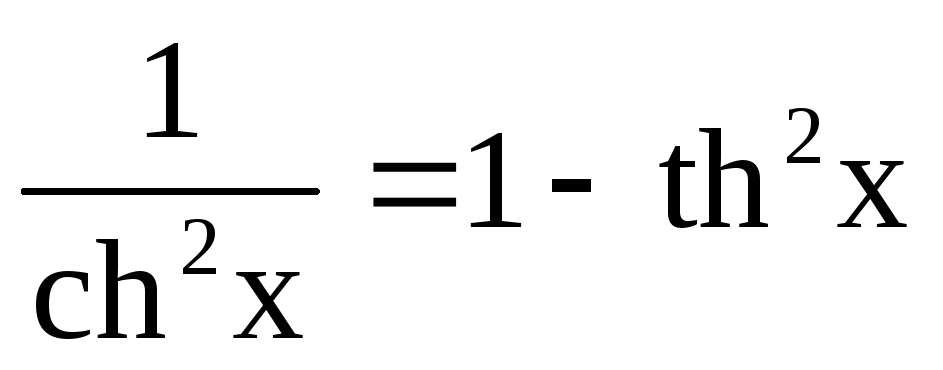
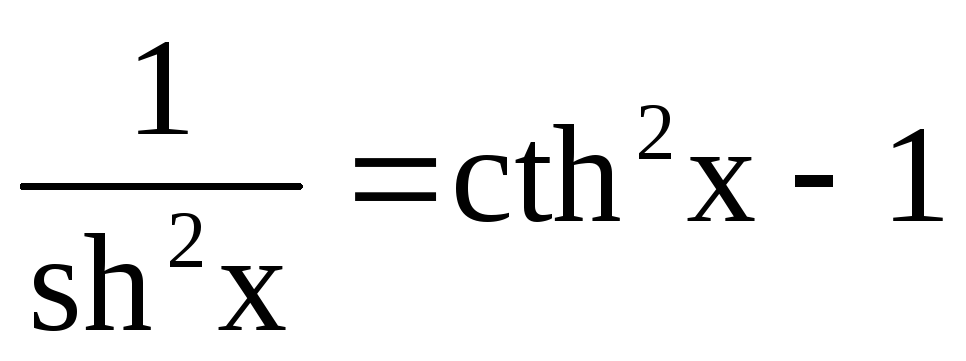 .
.
Приклад 34.
![]()
Рішення.
![]()
![]()
Приклад 35.
![]()
Рішення.
![]()
![]()
Приклад 36.
![]()
Рішення.
![]()
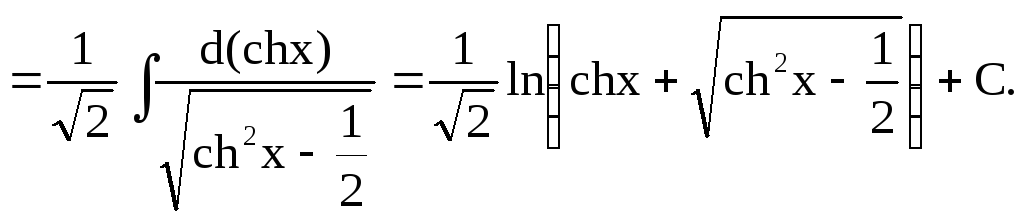
Приклад 37.
![]()
Рішення.
![]()
![]()
![]()
Інтегрування диференціальних біномів.
Вираз виду
![]() деm,n,p
– сталі раціональні числа, називається
диференціальним біномом. Російський
математик П.Л.Чебишев у 1853 р. показав,
що інтеграли від диференціального
бінома
деm,n,p
– сталі раціональні числа, називається
диференціальним біномом. Російський
математик П.Л.Чебишев у 1853 р. показав,
що інтеграли від диференціального
бінома![]() виражаються через інтеграли від
раціональної функції відносно нової
змінної лише в тому випадку, якщо одне
з чисел
виражаються через інтеграли від
раціональної функції відносно нової
змінної лише в тому випадку, якщо одне
з чисел![]() є цілим. Ці інтеграли зводяться до вже
розглянутих за допомогою таких
підстановок:
є цілим. Ці інтеграли зводяться до вже
розглянутих за допомогою таких
підстановок:
P – ціле число (додатне, від’ємне чи 0), виконуємо підстановку
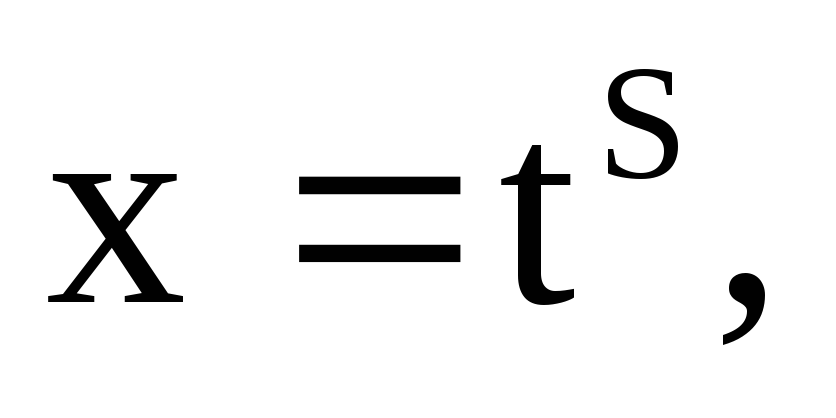 де s– найменший
спільний знаменник дробівmіn;
де s– найменший
спільний знаменник дробівmіn;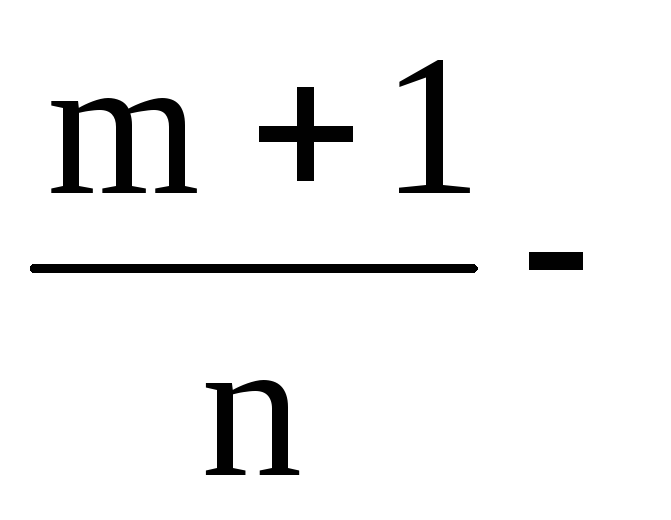 ціле
число (додатне, від’ємне
чи 0), виконуємо підстановку
ціле
число (додатне, від’ємне
чи 0), виконуємо підстановку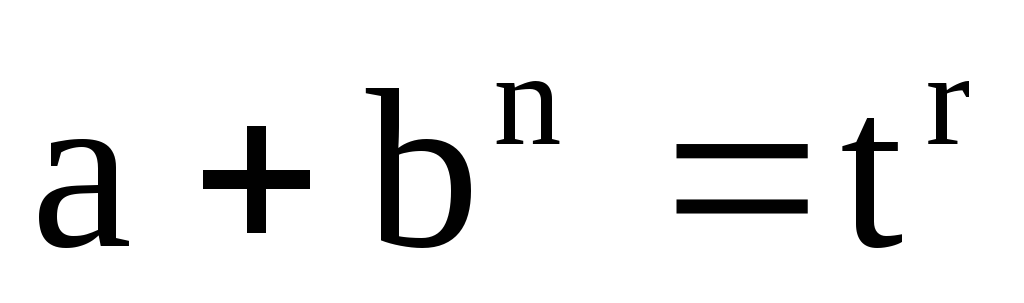 ,
деr– знаменник дробуp.
,
деr– знаменник дробуp.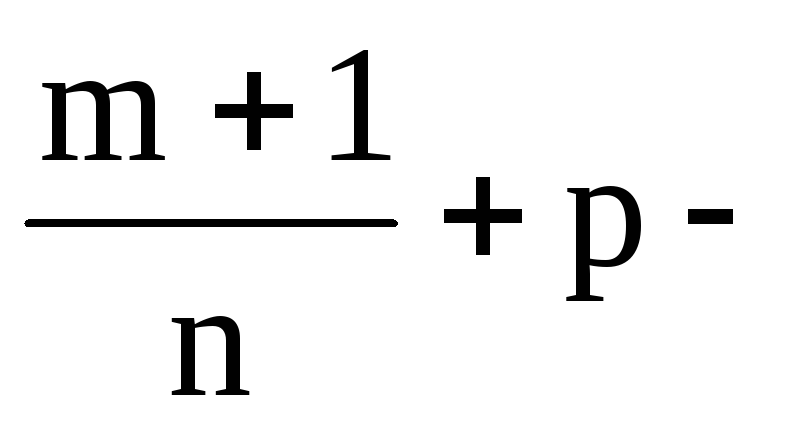 ціле
число (додатне, від’ємне
чи 0), виконуємо підстановку
ціле
число (додатне, від’ємне
чи 0), виконуємо підстановку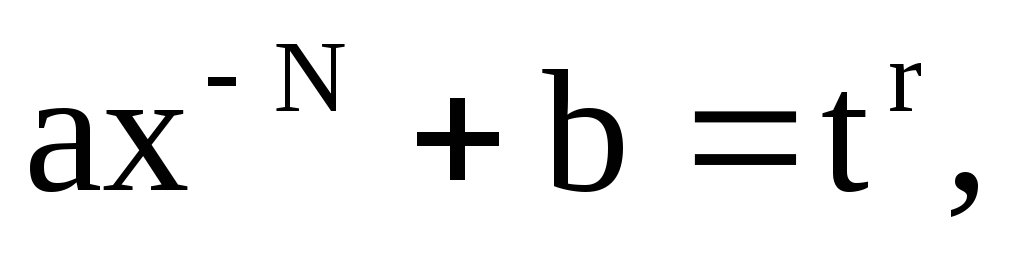 деr– знаменник дробуp.
деr– знаменник дробуp.
В інших випадках інтеграл від диференціального бінома через елементарні функції не виражається.
Приклад 38.
![]()
Рішення. Тут m=3,
n=2,
![]() Оскільки
Оскільки
![]() є ціле число, використовуємо
підстановку
є ціле число, використовуємо
підстановку
![]() тобто
тобто
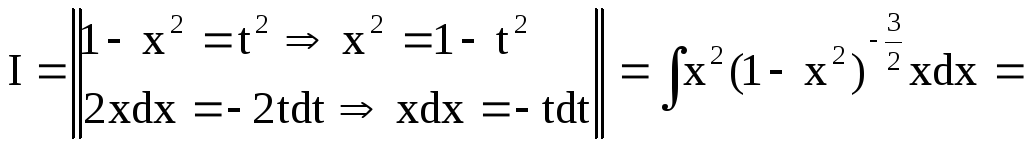
![]()
![]()
![]()
Приклад 39.
![]()
Рішення. Так як
![]() то
то![]()
![]() Оскільки
Оскільки![]() є ціле число, то виконуємо підстановку
є ціле число, то виконуємо підстановку![]() тобто
тобто
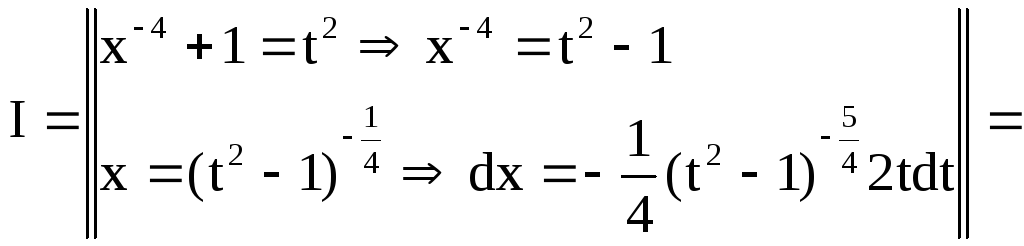
![]()
![]()
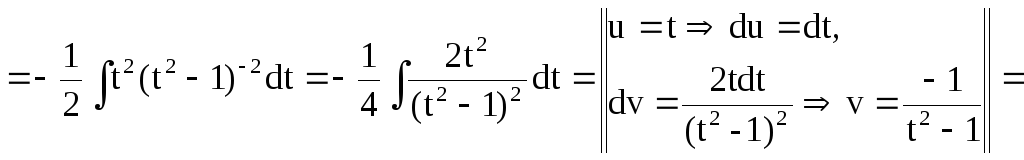
![]()
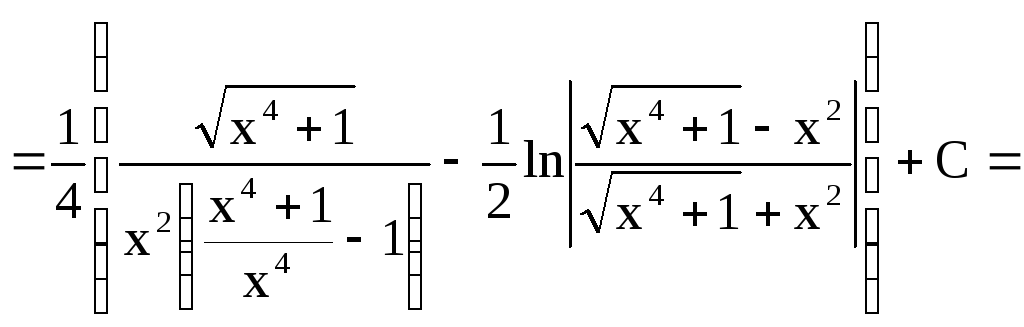

![]()
