3. Определение вероятности безотказной работы резервированного оборудования

Рисунок 1.9 – Зависимость вероятности безотказной работы системы P_c (t) от числа n и вероятности безотказной работы элементов P_i (t)

Для определения вероятности безотказной работы системы не­обходимо определить вероятности безотказной работы каждого элемента и по теореме умножения вероятностей их значения перемножить. В связи с тем, что вероятность безотказной работы каждого элемента меньше единицы, при боль­шом числе элементов вероятность безотказной работы системы значительно ниже вероятности безотказной работы каждого эле­мента, входящего в систему.

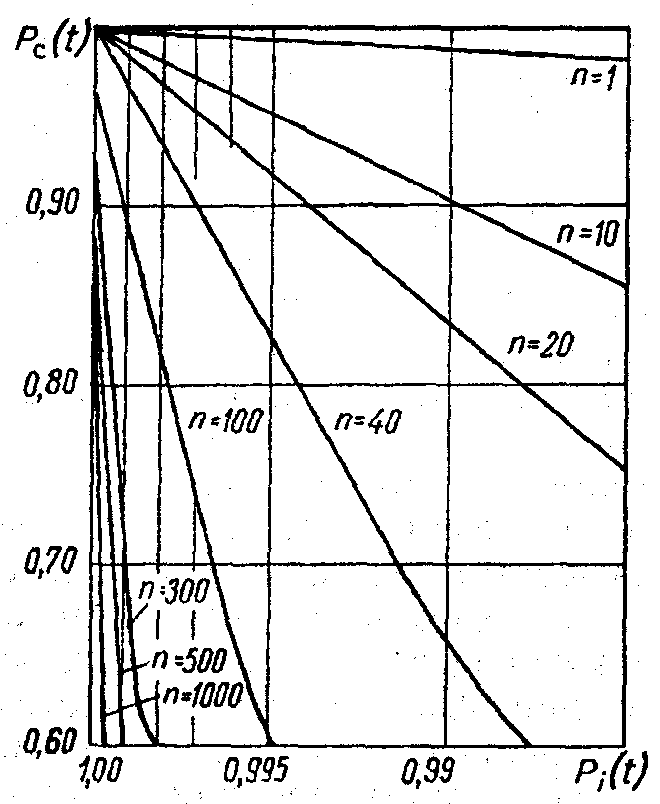
На рисунке 1.9 показана зависимость вероятности безотказной работы системы P_c(t) от числа n вероят­ности безотказной работы элементов P_i(t) при условии, что все вхо­дящие в систему элементы равнонадежны.

Повысить надежность системы можно путем снижения числа элементов или повышения вероятности их безотказной работы. Например, если система состоит из 50 элементов с вероятностью безотказной работы каждого элемента P_i(t)=0,9, то вероят­ность безотказной работы такой системы P_c(t)=0,9⁵⁰ =0,0052, если же система состоит из 100 элементов с той же вероятностью безотказной работы P_i(t)=0,9, то вероят­ность безотказной работы такой системы P_c(t)=0,9¹⁰⁰ = 0,00026.

Если же вероятность безот­казной работы элемента повы­сить до P_i(t)=0,999, то P_c(t)=0,999¹⁰⁰ =0,912.

Напрашивается простой вывод. Чем проще конструктивная схема машины или механизма, тем выше ее надежность при равной вероятности безотказ­ной работы элементов. Если упростить конструкцию аппарата не представляется возможным, то необходимо повышать вероятность безотказной работы составляющих элементов.

Рисунок 1.10 – Интегральные кривые безотказности системы с внезапными (1) и постепенными (2) отказами

По уравнению (1.8) опреде­ляют вероятность безотказной работы систем с внезапными отказами. Для систем же с по­степенными отказами при использовании этого уравнения получают заниженные результаты. Это объясняется тремя обстоятельствами.

Во-первых, в отличие от кривой P_c(t) (рис. 1.10), связанной с внезап­ными отказами, кривая P_c(t), связанная с постепенными от­казами, не начинается с t=0. Имеется участок нечувстви­тельности t₀, на котором вероят­ность безотказной работы эле­мента P_i(t)=1 и системы P_c(t)=1. На участке t₀ отказов не возникает. Это легко понять, так как, несмотря на рассеивание ин­тенсивности изнашивания или меры повреждения при усталостном разрушении, нельзя предста­вить, чтобы изделия были настолько некачественными, чтобы сразу же в начале работы деталь достигла предельного состояния или пол­ностью исчерпалась бы ее несущая способность в результате усталостного разрушения. При наличии зоны нечувствительности на уча­стке t₀ любые перемножения вероятностей безотказной работы эле­ментов обеспечивают вероятность безотказной работы системы, равную единице.

Во-вторых, нечеткость определения предельных показателей. При достижении предельного показателя деталь часто может еще некоторое время работать. Предельный параметр имеет некоторую свою зону нечувствительности.

В-третьих, если элемент системы отказал, достигнув предельно­го состояния одной из деталей, то при его разборке осматривают смежные детали и при опасности возникновения отказа их заменя­ют или ремонтируют.

Поэтому вероятность безотказной работы системы с постепен­ными отказами целесообразно определять по вероятности безот­казной работы худшего элемента, т.е.:

P_c(t) = P_imin (t), (1.30)

где P_imin – вероятность безотказной работы худшего элемента, входящего в сис­тему.

Пример.

Оценить вероятности безотказной работы двух систем с последователь­ным и параллельным соединением элементов. В системы входят два элемента. Ве­роятность безотказной работы первого элемента P₁(t)=0,8, второго P₂(t)=0,5. Вероятность безотказной работы системы с последовательно соединенными элементами по уравнению (1.8) будет равна:

P_c(t) = P₁(t) P₂(t) =0,8x0,5 =0,4.

Вероятность безотказной работы системы с параллельно соединенными эле­ментами по уравнению (9) будет равна:

P_c(t) =1-[(1-0,8)(1-0,5)] =0,9.

Из этого примера видно, что вероятность безотказной работы системы с последовательно соединенными элементами хуже худ­шего элемента, а с параллельно соединенными элементами лучше самого надежного элемента.

Используя уравнения (1.8) и (1.9), можно прогнозировать ве­роятность безотказной работы агрегатов и машин на стадии проек­тирования, например теплообменника. Для этого на основе данных по на­дежности деталей и сборочных единиц прототипа принимают веро­ятности безотказной работы отдельных элементов. Дета­ли и сборочные единицы с равными вероятностями безотказной работы группируют в блоки (табл. 1.4).

Таблица 1.4 – Вероятность безотказной работы основных деталей и сборочных единиц за время t

№ блока	Наименование деталей и сборочных единиц	Число деталей и cборочных единиц	Вероятность безот­казной работы
1	Фланцевое соединение	14	0,9999
2	Трубный пучок и трубная доска	8	0,9990
3	Метизы и др.	40	0,9970
4	Насос	3	0,9900
5	Поплавковый конденсатоотводчик	5	0,9280

Рисунок 1.11 – Блок-схема теплообменника с элементами:

а — последовательно соединенными; б— резервными

Составляют блок-схему теплообменника с последовательно соединен­ными элементами (рис. 1.11а) и рассчитывают вероятности безотказ­ной работы блоков и всего теплообменника по формуле (1.8):

P₁(t)=0,9999¹⁴=0,9986; P₂(t)=0,9990⁸=0,9920; P₃(t)=0,9970⁴⁰=0,8867; P₄(t)=0,9900³=0,97; P₅(t)=0,9280² =0,6882; P_то(t)=P₁(t)хP₂(t)хP₃(t)хP₄(t)хP₅(t) =0,5863.

Рассчитанную вероятность безотказной работы сопоставляют с нормативным значением P_то(t)≥P_то.нор(t)=0,8. При недостаточном уровне надежности анализируют блок-схему и определяют направ­ления ее совершенствования изменением конструкции материа­лов, технологии изготовления отдельных деталей и сборочных еди­ниц; введением резервных элементов.

В случае введения резервных элементов резервируют менее надежные четвертый и пятый блоки. Вводят тройное резервирование четвертого и пятикратное пятого блоков. Тогда, используя уравне­ние (1.9), пересчитываем вероятность безотказной работы четвертого и пятого блоков, получим:

P₄(t) =1-(1-0,97)³ =0,999; P₅(t)=1-(1-0,6882)⁵ =0,997;

P_то(t) =0,9986х0,9920х0,8867х0,999х0,997 =0,875, что пре­вышает нормативное значение.

Л. 12