„Будь-які спонтанні процеси в замкненій термодинамічній системі можуть відбуватися лише за умови, що ентропія системи при цьому не зменшується” :

(50)

Знак нерівності у (50) стосується нерівноважних термодинамічних процесів, знак рівності – рівноважних. Твердження (50) є однією з форм другого закону термодинаміки.

Другий закон термодинаміки, таким чином, регламентує ті термодинамічні процеси, які можуть відбуватися у замкненій термодинамічній системі без впливу ззовні, тобто відбуватися невимушено, спонтанно. Чи можливі процеси протилежні (50), в яких ентропія системи зменшується ( ), а сама система переходить з більш ймовірного до менш ймовірного термодинамічного стану? Принципово такі термодинамічні процеси можливі, вони не є забороненими законами термодинаміки. Втім вони не можуть відбуватися у замкненій ТД-системі спонтанно, отже, потребують зовнішнього впливу на термодинамічну систему.

Зауважимо, що для замкненої ТД-системи, що складається, припустимо, з двох підсистем, і під час спонтанного процесу з другого закону термодинаміки виникає:

(51)

тому, що ентропія системи є сумою ентропій її підсистем (ентропія є екстенсивною, тобто адитивною величиною). Проте, в замкненій термодинамічній системі додатково маємо:

(52)

Отже:

(53)

Припустимо, що тобто тепло отримує перша система від другої. Тоді й величина множника у круглих дужках має бути позитивною і тому . Отже, „у замкненій системі тепло спонтанно передається лише від тіла з більшою температурою до тіла з меншою температурою”. Це формулювання є іншим варіантом другого закону термодинаміки. Зверніть увагу на те, що тепло спонтанно (само собою) передається не від тіла з більшою внутрішньою енергією до тіла з меншою енергією, як можна було б помилково думати, а саме від більш нагрітого тіла до менш нагрітого, незалежно від того яке з них має більшу внутрішню енергію! Якщо підсистеми є у рівновазі між собою, то . Отже умова однаковості температур є необхідною (хоча й не достатньою) умовою термодинамічної рівноваги поміж підсистемами.

Таким чином, як перший, так і другий закони термодинаміки мають природне статистичне обґрунтування. Статистична фізика дозволяє нам не просто обґрунтувати ці закони, які лише постулювалися в термодинаміці, однак не доводилися в її межах, але й визначити фізичний зміст таких ключових термодинамічних понять як внутрішня енергія та температура системи.

• Теплові двигуни та холодильні машини

Тепловими машинами у технічній термодинаміці називають будь-який прилад, або устаткування, яке дозволяє циклічно перетворювати теплову енергію у механічну роботу.

Якщо запустити теплову машину у зворотному напрямі (тобто по оберненому циклу), то вона перетворюватиме механічну роботу зовнішнього джерела енергії у теплову енергію. Такі машини отримали назву теплових насосів, або холодильних машин.

Ц

Холодильник

Нагрівач

Рис.5.

иклічність дії теплової машини потребує того, аби кожна з них мала принаймні три основні складові частини: джерело теплової енергії (нагрівач), робоче тіло, і холодильник (рис.5). Робоче тіло отримує тепло від нагрівача, здійснює певну роботу , а далі передає частину тепла холодильнику і за рахунок такої віддачі частини тепла, отриманого від нагрівача, повертається у початковий стан. Далі весь цикл повторюється. Отже нагрівач, холодильник та робоче тіло є невід’ємними складовими частинами кожної теплової машини, або теплового насосу (холодильної машини). Ефективність (к.к.д) теплової машини у загальному випадку дорівнює:

(54)

Ефективність теплової машини може збільшуватися лише двома способами, які передбачають: зменшення кількості тепла відданого холодильнику ( ) та збільшення кількості тепла отриманого від нагрівача ( ).

Обидва шляхи, зрозуміло, мають певні обмеження. Зокрема важливим є те, що загалом обійтися без витрат тепла на холодильник (тобто покласти , отже й ) не можна, хоча б тому, що така теплова машина не змогла б здійснювати циклічного процесу, в якому робоче тіло час від часу повертається у початковий стан.

П

Рис.6.

итання про найвигідніший цикл теплової машини поставив і вирішив у першій половині ХІХ сторіччя французький військовий інженер Саді Карно у своїй роботі „Про рушійну силу вогню”. Карно запропонував спеціальний цикл (a-b-c-d,рис.6), який складається з двох ізотермічних процесів (a-b,c-d) підводу та відбору тепла від робочого тіла, та двох адіабатичних (ізоентропійних) процесів (b-c,d-a) розширення та стискання робочого тіла (рис.6). Традиційно цикл Карно зображують в координатах (тиск-об’єм), хоча він значно простіший та зрозуміліший в інших координатах (ентропія-температура).

Розглянемо цикл Карно детальніше за його чотирма етапами:

1. В ізотермічному процесі a-b ( 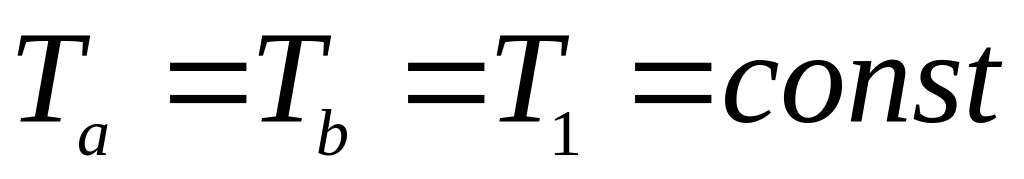) при температурі відбувається підвід тепла до робочого тіла від нагрівача. Робоче тіло при цьому згідно з першим законом термодинаміки перетворює все отримане тепло у позитивну механічну роботу, оскільки в ізотермічному процесі, як відомо, внутрішня енергія лишається незмінною. Робоче тіло в процесі a-b розширяється ( ).

2. В адіабатичному процесі b-c робоче тіло від’єднують від нагрівача і без втрат тепла ( , ) робоче тіло здійснює додаткову позитивну роботу за рахунок зменшення внутрішньої енергії, як це завжди має місце в адіабатичному процесі. Температура тіла при цьому зменшується від до . Робоче тіло в процесі продовжує розширюватися ( )

3. В ізотермічному процесі c-d ( ) робоче тіло з’єднують з холодильником із температурою і відбирають у нього певну кількість тепла . Робоче тіло при цьому стискається ( )

4. Нарешті в адіабатичному процесі d-a робоче тіло при незмінній ентропії (отже, без витрат тепла) нагрівається від температури до температури і відновлює запас внутрішньої енергії до початкового значення (робоче тіло стискається в цьому процесі ).

Після цих чотирьох етапів, цикл може повторюватися безкінечно. Кожен раз за один цикл буде виконуватися робота: .

Повна зміна ентропії в циклі, так само як і зміна внутрішньої енергії дорівнює нулю. Записуючи повну зміну ентропії в циклі Карно як суму змін в кожному з чотирьох етапів, можемо формально отримати вираз:

(55)

де ми врахували, що .

Користуючись рівнянням Клаузіуса маємо:

(56)

де врахували ізотермічність процесів (незмінністю температур). Підставляючи (56) у (55) маємо для циклу Карно наступну умову:

(57)

з якої вже неважко отримати вираз для коефіцієнту корисної дії циклу Карно: . Остаточно маємо формулу Карно:

(58)

ефективність циклу Карно, таким чином, визначають лише температури нагрівача та холодильнику . Зауважимо, що формула (58) отримана без жодних припущень щодо природи робочого тіла, отже, його властивості не є важливими для циклу Карно.

Теорема Карно стверджує:

„жодна теплова машина, працююча по будь-якому термодинамічному циклу не може мати к.к.д вищий від (58), якщо вона працює поміж нагрівачем та холодильником з температурами відповідно”.

Важливим наслідком теореми Карно є неможливість такого циклу, температура холодильника якого би дорівнювала абсолютному нулю температури: . Оскільки при умові нульової температури цикл Карно мав би , що неможливо з огляду на причини, розглянуті вище. Тому неможливість теплового циклу, для якого (отже, ), а звідси і циклу Карно, для якого , вважають третьою формою вже знайомого нам по двох інших формулюваннях другого закону термодинаміки. Отож недосяжність абсолютного нуля температур, є прямим наслідком другого закону термодинаміки.