ответы мо

1. Оптимальный-наилучший.

2. Недопустимы выражения «самый оптимальный» и т.п., потому что лучше наилучшего не бывает.

3. Оптимизация в широком смысле-выбор наилучшего варианта из мн-ва альтер-х.

4. Оптимизация в узком смысле-миним-я или максим-я ф-й.

5. Наиболее полно используют возможности современной вычислительной техники численные методы.

6. Впервые ввёл в математике термин «оптимизация» Лейбниц.

7. Синоним МО-математическое программирование.

8. Невозможно прделожить один метод, один-во эффект-й для всех задач, поэтому изучается мн-во методов.

9. Предмет учебной дисциплины «Методы оптимизации»-ЧМ организации.

10. Параметры оптимизации-переменные параметры, т.е. те независ-е перем. в задаче оптимизации, кот. можно произвольно менять. Вектор переменных параметров-набор всех перем-х парам. x=(x_1, x_2, ..,x_n)^T, n=dimX.

11. Пространство параметров x_iєR=(-∞;+∞)-мн-во всех векторов Х(Rⁿ). Размерность-Rⁿ=RxRx…xR(n раз).

12. Допустимая область-включает ограничения в виде равенств и неравенств: D={x|g_k(x)≤0,k=1,p; h_j(x)=0, j=1,r}

13. Критерий качества-любой функ-нал, кот представляет качество системы.

14. Целевая функция-критерий качества с указанием признака его оптим-ции(миним-ции или максим).

15. Задача оптимизации-миним-ции целевой ф-ии при отсутствии или наличии огр-ний.

16. Решение задачи оптимизации: x^*-вектор, удовлет-й усл: f(x^*)=min f(x).

17. МО-ЧМ, кот позвол-т получить реш-е зад-и опт-ии эфф-м путем без полного перебора вар-тов

18. Задача Дидоны: Треб. Max площадь S(x)=x₁*x₂ при огранич. периметра l(x)=x, l(x)=2x₁+x₂. Задача нелин-го прогр. S(x)→max, 2x₁+x₂=C.

19. Задача нелинейного программирования это задача на условный минимум с ограничениями типа неравенств.

20. Задача оптимального распределения ресурсов: требуется из m рес-ов, запасы кот. a₁,..,a_m, изготовить n изделий x₁,..,x_n. C_i-стоимость продажи x_i, b_ij-норма расхода jго рес-са для произв iго изделия. Необх max прибыль предпр. f(x)=Σc_ix_i, Σb_ijx_i≤a_j, j=1,m, x_i≥0, i=1,n. Зад. лин-г прогр-я.

21. Общей задачей лин. прогр-я называется задача, которая состоит в определении макс. (мин.) значения функции?

22. Транспортная задача: миним-ции перевозок различ-х грузов из пункта произв-ва в п. потребл. при огр-ях этих грузов как в п. произв, так и в п. потребл. Лин.програм.

23. Задача оптимизации ракеты: Цел ф-я f(x)-модель стоимости ракеты, включ. 26 огран-й. dimx=25. Цел ф-я и огран. нелин-ые. f(x) →min, xєD. Было получ реш-е x^*, для кот. f^*=f(x^*)=2330000$. Чичинадзе разраб. метод ψ-преобр и нашел глоб мин f^**=f(x^**)=1359000$.

24. Полезность решения задач опт:

25. Основные признаки классификации МО: применяемые средства, типы задач опт-ции, пор-ку проив-х

26. Классификация МО по применяемым средствам: аналит-е(методы мат анализа), графич-е, числ-е(прим вычисл техники), эксперемент-е, полного перебора вар-тов.

27. Классификация МО по математической формулировке задачи оптимизации: одномер поиска, многомер безусл опт-ии, условной опт-ии, лин програм-я, выпуклого прогр-я, миним-ии суммы квадратов, дискр прогр-я.

28. МО по порядку используемых производных целевой функции: 0го(прямого поиска), 1го(первая произв ▼f(x)-вектор произ-х), 2го.

29. МОП для задачи 0го.

30. Т x^* назыв т миним ф-ии, если в ней достиг найменшее знач по сравн-ю с др т нек-й её окрестности f^*=f(x^*).

31. Теорема Ферма: если диф-я ф-я f(x) в т x^* имеет экстремум, то f’(x^*)=0.

32. Точки, в кот произв-я обращ-ся в 0 назыв стационарными.

33. Найменьший минимум многоэкстр-й ф-ии назыв глобал, остальные-локал-е.

34. Необходимый признак сущ-я экстр ф-ии одной перем: произв-я обращ-сь в 0..

35. Необх и дост-й признак сущ-я экстр ф-ии одной перем: изменение знаков произв при переходе через данную точку.

36. Если для f’’(x) f’(x^*)=0, а f’’(x^*)≠0(>0-min, <0-max)

37. Строго убывающими и строго возрастающими явл ф-ии, если для знач u<v f(u)<f(v).

38. Унимодальная ф-я-для кот сущ-т такое знач аргум x_*левее кот ф-я убывает, а правее-возраст.

39. Выпуклая-ф-я, если для любого λє[0,1] и любых 2х т u и v вып-ся f(λu+(1-λ)v)≤ λf(u)+(1-λ)f(v). Если нерв-во строгое-строго выпук

40. Аналогично выпукл, только знак ≥.

41. Особенность выпуклой функции, имеющей минимум: график выпуклой функции лежит под хордой, соединяющей две любые ее точки.

42. Инт-л неопред-интер-л [a,b]cR, кот содержит неизв т миним x^*.

43. Этапы МОП: поиск инт-ла неопр, его уменьшение.

44. Чтобы определить инт-л неопр необх 2 точки.

45. Чтобы уменьшить этот интервал необх 2 внутр точки.

46. Правило исключ инт-в: если для [a,b], содерж-го т мин x^* со знач ф-ии f^*=f(x^*) известны 2 внутр точки u и v такие, что u<v, f_u=f(u), f_v=f(v), то при усл f_u<f_v x^*є[a,b], а при усл f_u ≥f_v xє[u,b].

47. Метод Свенна предназначен для поиска инт-ла неопр методом удвоения шага

48. Если ф-я в найденной точке f₁<f₀, то шаг удваивается в полож-м напр, иначе идем в отриц-м напр-ии.

49. Шаги вычисл до тех пор, пока знач ф-ии уменьш.

50. Метод Свенна: пусть треб найти инт неопр в т мин унимод ф-ии f(x). Зададим нач т поиска x₀ и вычисл f₀=f(x₀)На осн зад-го шага h>0 найдем x₁=x₀+h и вычисл f₁=f(x₁). Если f₁<f₀, то вып поиск в полож направл путем удвоения шага по ф-ле x_k+1=x_k+2^kh. Если f₁≥f₀, то x₂=x₀-h и f₂=f(x₂). Если f₂<f₀, то вып-ся шаги в отриц напр по ф-ле x_k+1=x_k-2^k-1h.

51. Метод Свенна 0 пор-ка.

52. Пассивная стратегия опред-ся тем, что т поиска x_kє[a,b] зад-ся заранее до вычис знач-й ф-ии в этих т.

53. Назначение метода равномерного поиска-уменьш инт-ла неопр.

54. Метод равномерного поиска: пусть известен инт неопр и задано допуст число вычисл ф-ии n. Разделим [a,b] длинны L=b-a равномер и т на n+1частей длины δ=L/n+1, x_k=a+k* δ, f_i=minf_k. Конечный инт неопр L_n=2δ=2L/n+1.

55. Эффективность метода равномерного поиска опред-ся отнош длин конечного инт неопр к начальному r_n=L_n/L=2/n+1.

56. Преимущество равномер поиска-позволяет вычислить миним даже многоэкстрем-й цел ф-ии в зад-м инт с гарантир-й точностью. Недостатки-для унимод ф-й сущ-т намного более эфф методы поиска.

57. Последовательные МОП отличаются выбором целевой ф-ии.

58. Назначение метода дихотомии: уменьшение инт-ла неопр.

59. Основные принципы метода дихотомии:

60. Метод дихотомии: пусть известен инт неопр длинны L=b-a и для уменьш инт-ла разделим его на т u и v. По правилу искл инт-лов остан-ся новый инт неопр [a,v] или [u,b]. u=c- δ, v=c+ δ. Если f_u<f_v, то [a,v] новый инт неопр, иначе [u,b]. Длинна нового инт L₂=L/2 + δ. Чтобы длинна нового инт была найм δ должно быть как можно меньше.Т. обр., на каждой итер 2жды вычисл знач ф-ии и при дост малом δ инт неопр <в 2р.

61. Для повышения эфф-ти поиска полаг-т l₁=l₂, т.е. u и v зад-ся симм-но относ серед инт-ла c=a+b /2 на расст δ.

62. Метод дихотомии нулевого порядка.

63. Основным недост метода дих-мии явл его завис от парам δ: при большом знач метод теряет эфф-ть, а при малом т u и v могут оказ неразлич и инт неопр м.б. потерян. Также недост явл вычисл знач ф-ии в 2х т на каждой итер. Дост-м явл высокая эфф-ть по сравн с методом равномер поиска и простота алгоритма.

64. Назначение метода деления интервала пополам: уменьш инт-ла неопр.

65. Метод деления интервала пополам: разделим инт неопр длинны L=b-a пополам. Т c=a+b /2 и вычисл f_c=f(c). Разделим левый инт-л [a,c] пополам и u=a+c /2, f_u=f(u). Если f_u<f_c, то (c,b] не содержит т мин x^* и его можно исключ. Новый инт-л [a,c] с извест средней т (v,f_v). Иначе [c,b] пополам, т b=c+b /2, f_b=f(b). Если f_v<f_c, то [a,c) искл, [c,b]-инт неопр. Иначе искл крайние инт-лы [a,u) и (v,b], а [u,v] инт неопр, включ ср т (c,f_c).

66. Эффек-ть метода: в найл случае, когда выбир левая половина инт-ла, длинна инт-ла неопр после n вычисл ф-ии f_n=L/2^n-1. В противном сл L_n=L/2^(n-1)/2, r_n=L_n/L, 1/2^n-1≤r_n≤1/2^(n-1)/2.

67. Метод деления интервала пополам нулевого пор-ка

68. Достоинства метода деления инт-ла пополам: по сравн с дихот данный метод в найл случае использ-т примерно вдвое меньшее число вычисл, а в найхуд-только на 1 больше; не зависит от δ и в нем примен только операции сложения и деления на 2; облад высокой надежностью. Недостаток-более сложный алгоритм, а также вычисл 2х зач ф-ии в найхуд случае для каждой итер.

69. Числа Фибоначчи вычисл по ф-ле F_n=F_n-1+F_n-2

70. 10 первых чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.

71. Cвойства чисел Фибоначчи: F_n²-F_n-1F_n+1=(-1)ⁿ; F_n-1F_n-2-F_nF_{n -3} =(-1)ⁿ.

72. Формула Бине для чисел Фибоначчи:

73. Назначение метода Фибоначчи: уменьш инт-ла неопр.

74. Метод Фибоначчи: инт неопр длинны L=b-a дел 2мя т x₁ и x₂, симм-ми относ центра инт-ла, после чего прим правило исключ инт-лов. На послед-х итер оста-ся одна изв-я внутр т инт-ла x_k, а след т x_k+1 нах-ся симм-но изв-й внутри т. На послед итер после n вычисл-й ф-ии ост-ся инт неопр длинны L_n, кот получ также, как и в дихот.

75. Общая формула для длин интервалов неопределенности в методе Фибоначчи: L_n-j=F_j+1L_n-F_j-1δ, j=1,n-1.

76. В методе Фибоначчи для начала поиска необх найти полож первой т деления исх инт, кот должна лежать на расст L₂ от конца инт. При j=n-2 получим L₂=F_n-1L_n-F_n-3 δ.

77. Метод Фибоначчи явл теор самым эфф-м методом уменьш инт, т.к. на всех итер кроме 1й вычисл только 1 знач. R_n=1/F_n

78. Метод Фибоначчи 0го пор-ка.

79. Недостатком метода Фиб явл зависимость от δ и треб-ся задавать число n. Преимущ-найбольшая эфф-ть.

80. Задача «о делении отрезка в крайнем и среднем отношении» привела к появл ЗС: разделить отрезок AB тC в таком отнош, чтобы длина большей части отр CB так относ к длине меньшей части AC, как длина всего AB к большей части CB.

81. Уравнение ЗС: AB/CB=CB/AC, AB=AC+CB, x=AC+CB /CB=1+AC/CB=1+1/CB/AC=1+1/x, x²=x+1, корень .

82. Численное представление ЗС .

83. Свойства ЗС: обратное ему число на осн x²=x+1 можно получить вычит-ем единицы, любая целая степень ЗС равна сумме пред.

84. Связь между числами Фиб и ЗС:

85. Назначение метода ЗС: уменьш инт-ла неопр.

86. Метод ЗС: 2 первые т дел x₁=b-tL, x₂=a+tL. В этих т вычисл знач ф-ии f₁=f(x₁), f₂=f(x₂) и на осн сравн-я этих знач по прав искл инт-в в ост-ся инт-л [a,x₂]=>(f₁<f₂), [x₁,b]=>(f₁>f₂). После 1й итер имеем меньший инт неопр с 1 внутр т, кот делит новый инт также по ЗС. На посл итер-х наход-ся только 1 внутр т, симм-я оставш-ся т относ-но центра. Итер до тех пор пока L_n<E.

87. Как и метод Фиб, ЗС использ принцип сиим-ии для 2х внутр т деления инт неопр.

88. Метод ЗС обладает преимущ-м перед Фиб, потому что в нем вычисл можно прекратить в любой момент, т.к. точки, в кот пров-ся вычисл не зависят от их общего числа n.

89. Поиск минимума в методе ЗС начин с определ 2х первых т дел-я x₁=b-tL, x₂=a+tL и вычисл знач ф-ии f₁=f(x₁), f₂=f(x₂).

90. Эффективность метода ЗС: L_n=t^n-1L=L/^n-1, r_n=1/^n-1.

91. Сравнение методов Фиб и ЗС: lim LF_n/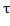^n-1L=lim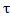ⁿ⁺¹/=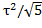. Т.обр, при больших n методом ЗС будет найден инт неопр на 17% больше, чем методом Фиб.

92. Метод ЗС 0го пор-ка.

93. Дост-во метода ЗС:высокая эфф-ть, практ-ки такая же, как у Фиб и дост-но постой алг, не треб-й задания числа вычисл n. Недостаток: завис от иррац-го числа t, кот необх задавать с макс возм-й точностью, иначе внутр т инт-ла могут изменить порядок и инт-л будет утерян, снижается надежность метода.

94. Назначение метода адаптации шага: уменьш инт-ла неопр.

95. Метод адаптации шага: зад-ся нач т x₀, r₀=0, h₀. Из нач т нах-ся пробная т поиска y₁=x₀+h₀, g₁=f(y₁). Все итер провод-ся по ф-ам y_k+1=x_k+h_k, g_k+1=f(y_k+1). После этого нах-ся лучшая т поиска (x_k+1, fk+1). В завис от сравн новой и лучшей точек и знач предыд множ шага, вычисл знач нового множ-ля

96. Шаг поиска в методе адаптации шага изм-ся по ф-ле h_k+1=h_k * r_k+1.

97. Метод адаптации шага 0го пор-ка.

98. Дост метода адапт шага: алг проще метода Свенна или дел инт пополам, не связан ни с какими парам, а основан на опер-х слож и умнож на степени 2ки, работает надежно и позв нах-ть мин цел-й ф-ии со сверхвысокой точностью.

99. Группы методов уменьшения инт неопр: 1)требующие задания инт неопр , ф-ии одной перем-равномер поиск, дихот, дел пополам, Фиб, ЗС. 2)не треб зад-я инт неопр-адапт шага.

100. Сравните эффективность методов уменьшения интервала неопределенности.

r	МРП	МД	МДИП	МФ	МЗС
10-1	19	8	[5; 9]	6	6
10-2	199	14	[8; 15]	11	11
10-3	1999	20	[11; 21]	16	16
10-4	19999	28	[15; 29]	20	21
10-5	199999	34	[18; 35]	25	25

По этой таблице видно, что теоретически самым эффективным методом умень-шения интервала неопределенности является метод Фибоначчи. Незначительно уступает ему в эффективности метод золотого сечения.

101. Какое назначение метода бисекции?

применяется для уменьшения интервала неопределенности с помощью вычисления производной целевой функции в средней точке интервала и часто используется для повышения надежности методов аппроксимации и интерполяции первого порядка.

102. На каких свойствах производной основан метод бисекции?

если мы ищем ноль, то на концах отрезка функция должна быть противоположных знаков. Разделим отрезок пополам и возьмём ту из половинок, на концах которой функция по-прежнему принимает значения противоположных знаков. Если значение функции в серединной точке оказалось искомым нулём, то процесс завершается.

103. По какому принципу уменьшается интервал неопределенности в методе бисекции?

На каждой итерации происходит уменьшение интервала неопределенности в 2 раза с помощью вычисления производной целевой ф-ции. При этом по правилу исключения интервалов исключается правая или левая часть интервала в зависимости от значения ф-ции и произв в средней точке. Итерации продолжаются до тех пор, пока длина интервала неопределенности не станет меньше заданного значения.

104.Опишите метод бисекции.

В этом методе вычисляются средняя точка интервала , а также значения функции и ее производной в средней точке: . Если , то найдена точка минимума , и вычисления прекращаются. Если , то исключим интервал [a,c), не содержащий точку минимума, полагая a=c. Если же , то исключим интервал (c,b], полагая b=c. Вычисления продолжаются, пока длина интервала неопределенности L=b-a превосходит допустимую погрешность L>E.

105.Какова эффективность метода бисекции?

. Соответствует методу дихотомии.

106.Какого порядка метод бисекции? Первого

107.Какие преимущества и недостатки метода бисекции?

Недостатки: в наихудшем случае может потратить только на одно вычисление функции больше, чем метод дихотомии.

Преимущества: в наилучшем случае он использует почти вдвое меньшее количество вычислений. К тому же в методе применяются только простые арифметические операции сложения чисел и деления на два.

108.Какое назначение методов квадратичной интерполяции?

Минимизации унимодальной целевой функции с целью поиска точки минимума функции.

109.Какие основы методов квадратичной интерполяции?

Основаны на аппроксимации целевой функции квадратичным полиномом , где коэффициенты определяются по значениям целевой функции и ее производных.

110.Выведите формулу квадратичной интерполяции для точки минимума.

Дифференцируем равенство , и получаем

По необходимому условию существования экстремума получим точку минимума параболы .Дальше определить коэф.

111.Какое назначение метода квадратичной интерполяции с тремя точками?

При помощи аппроксимации f(x) по 3 ее точкам квадратичным полиномом осущ поиск точки минимума этого функции точкой минимума этого полинома.

112.Опишите метод квадратичной интерполяции с тремя точками.

Первые 3 точки находим по м.Свенна: . Подставляем эти значения в ур.параболы.:сист. .Решая сист от параметров и подставив их в получим т. Минимума . Далее отбрасывается часть инт, где нет миним. Итер продолжается по двум последним формулам, пока расстояние больше погрешности.

113.Как начинается поиск минимума в методе квадратичной интерполяции с тремя точками?

Первые 3 точки находим по м.Свенна: . Дифференцируем равенство , и получаем Получаем т минимума . Определяем коэф.

114.Какого порядка метод квадратичной интерполяции с тремя точками?

Нулевого.

115.Какие преимущества и недостатки метода квадратичной интерполяции с тремя точками?

Преим:Легкие математ операции, нулевой порядок

Недост: Вледствии ошибок округления при выч минимума может оказаться, что значение окажется вне интервала неопределенности.

116.Какое назначение метода квадратичной интерполяции с двумя точками?

При помощи аппроксимации f(x) по 2 ее точкам квадратичным полиномом осущ поиск точки минимума этого функции точкой минимума этого полинома.

117.Опишите метод квадратичной интерполяции с двумя точками.

Первые 2 точки находим по м.Свенна: . Вычислим знач производной функ. На одном из концов Подставляем эти значения в ур.параболы.и ее произв.:сист.

.или

. Решая одну из систем нах.парам и вычисл . Если , то найдена точка минимума , и вычисления прекращаются. Если , то исключим интервал [a,u), не содержащий точку минимума, полагая a=u, функ и производные равны. Если же , то исключим интервал (u,b], полагая b=u, функ и производные равны. Вычисления продолжаются, пока длина интервала неопределенности L=b-a превосходит допустимую погрешность L>E.

118.Какого порядка метод квадратичной интерполяции с двумя точками?

первого

119.Какие преимущества и недостатки метода квадратичной интерполяции с двумя точками?

Преимущества: простота СЛАУ

Недостатки: Вычисление производных

120.Какое назначение метода секущих?

При помощи аппроксимации f(x) по 2 ее точкам квадратичным полиномом осущ поиск точки минимума этого функции точкой минимума этого полинома.

121.Как начинается поиск минимума в методе секущих?

Первые 2 точки и на концах интервала неопределенности найдем по алгоритму метода Свенна. Вычислим значения производных в этих точках.Сост сист уравнений . Получим ф для выч т миним .

122.Опишите метод секущих.

Первые 2 точки и на концах интервала неопределенности найдем по алгоритму метода Свенна. Вычислим значения производных в этих точках.Сост сист уравнений . Получим ф для выч т миним . . Если , то исключим интервал [a,u), не содержащий точку минимума, полагая a=u, функ и производные равны. Если же , то исключим интервал (u,b], полагая b=u, функ и производные равны. Вычисления продолжаются, пока длина интервала неопределенности L=b-a превосходит допустимую погрешность L>E.

123.Какого порядка метод секущих?

Первого

124.Какие преимущества и недостатки метода секущих?

Преим: Простота формул

Недост: медленная сходимость при минимиз невыпуклой ф-ции, диф функции

125.Какое назначение метода Ньютона?

При помощи аппроксимации f(x) по ее точке квадратичным полиномом осущ поиск приближением точки минимума этого функции точкой минимума этого полинома.

126.Выведите итерационную формулу метода Ньютона.

127.Опишите метод Ньютона.

Первую точку a на конце интервала неопределенности [a, b] со

значением целевой функции fa = f (a) найдем по алгоритму метода

Свенна. Вычислим значения первой и второй производных в этой точке f’_a= f ‘(a) и f¢¢_a = f ‘‘(a) . Дифференцируя равенство (4.2), имеем q¢¢(x) = 2a .

составим систему уравнений:

Решая эту систему и подставляя найденные значения коэффициентов

a и b ,получим формулу для вычисления точки минимума

Эта формула геометрически соответствует нахождению точки пересе-

чения с осью абсцисс Ox касательной, проведенной из точки a гра-

фика функции f ¢(x) , поэтому ее называют формулой касательной.

Затем вычислим fu = f (u) , f’u f (u) и f’’u f (u). Если , то найдена точка минимума , и вычисления прекращаются. В противном сл a=u и прим формулу

Вычисления продолжаются, пока расстояние между двумя последовательными точками интерполяции превышает допустимую погрешность e .

128.Какого порядка метод Ньютона? Второго

129.Какие преимущества и недостатки метода Ньютона?

Преим: Простота формул, а также его быстрая сходимость

Недост: Необход использ вторых частных производных, а также для выпуклых функ может расходиться.

130.Какое назначение методов кубической интерполяции?